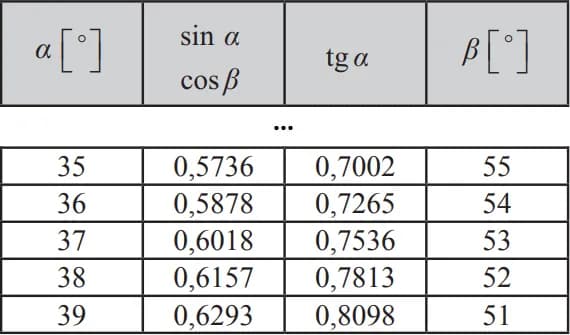
Tg w fizyce oznacza tangens, jedną z kluczowych funkcji trygonometrycznych. Funkcja ta wyraża stosunek długości boku przeciwległego do kąta ostrego w trójkącie prostokątnym do długości boku przyległego. Można ją również zapisać jako iloraz sinusa i cosinusa danego kąta: $$\text{tg}\alpha = \frac{\sin\alpha}{\cos\alpha}$$. Tangens ma ogromne znaczenie w różnych dziedzinach fizyki, takich jak analiza ruchu, optyka oraz mechanika. Dzięki tej funkcji jesteśmy w stanie rozwiązywać złożone problemy związane z siłami i momentami, co jest niezbędne w inżynierii oraz geodezji.
W codziennym życiu tangens znajduje zastosowanie w wielu praktycznych sytuacjach, na przykład przy wyznaczaniu wysokości obiektów na podstawie pomiaru kątów i odległości. Wzór $$h = d \cdot \text{tg}\alpha$$ pozwala na obliczenie wysokości, gdzie $$d$$ to odległość horyzontalna do obiektu, a $$\alpha$$ to kąt nachylenia. Oprócz tego, funkcja tangensa jest okresowa i ma swoje ograniczenia, ponieważ nie jest określona dla kątów takich jak 90° czy 270°. Zrozumienie tangensa jest kluczowe dla analizy zjawisk fizycznych, które nas otaczają.
Kluczowe wnioski:
- Tg oznacza tangens, funkcję wyrażającą stosunek boków w trójkącie prostokątnym.
- Można go zapisać jako iloraz sinusa i cosinusa: $$\text{tg}\alpha = \frac{\sin\alpha}{\cos\alpha}$$.
- Tangens jest używany w analizie ruchu, obliczeniach optycznych i mechanice.
- W geodezji tangens pomaga wyznaczać wysokości obiektów na podstawie kątów i odległości.
- Funkcja tangensa ma okres $$\pi$$ radianów i asymptoty pionowe dla kątów, gdzie cosinus wynosi zero.
Co oznacza tg w fizyce i jak jest definiowane w matematyce?
W fizyce symbol „tg” oznacza tangens, jedną z podstawowych funkcji trygonometrycznych. Funkcja ta wyraża stosunek długości boku przeciwległego do kąta ostrego w trójkącie prostokątnym do długości boku przyległego. Można ją zdefiniować matematycznie jako: $$\text{tg}\alpha = \frac{\sin\alpha}{\cos\alpha}$$. Tangens jest istotnym narzędziem w matematyce, które znajduje zastosowanie w różnych dziedzinach, w tym w fizyce.
Warto zwrócić uwagę na kilka kluczowych właściwości tangensa. Funkcja ta jest okresowa, co oznacza, że powtarza swoje wartości w regularnych odstępach. Okres tangensa wynosi $$\pi$$ radianów. Dodatkowo, tangens ma asymptoty pionowe w miejscach, gdzie cosinus kąta wynosi zero, co oznacza, że funkcja nie jest określona dla kątów takich jak 90° czy 270°. Te cechy sprawiają, że tangens jest unikalny w porównaniu do innych funkcji trygonometrycznych, takich jak sinus czy cosinus, które mają inne właściwości okresowe i zakresy.
Tangens jako funkcja trygonometryczna i jego właściwości
Tangens ma kilka kluczowych właściwości, które odgrywają ważną rolę w matematyce i fizyce. Przede wszystkim, jego dziedzina jest ograniczona do wszystkich kątów, z wyjątkiem kątów, dla których cosinus wynosi zero. Oznacza to, że tangens jest zdefiniowany dla wszystkich kątów, z wyjątkiem 90° i 270°. Zakres funkcji tangens obejmuje wszystkie liczby rzeczywiste, co czyni ją funkcją, która może przyjmować dowolne wartości.
Jedną z istotnych cech tangensa jest jego monotoniczność. Funkcja ta jest rosnąca w każdym przedziale, w którym jest zdefiniowana. Porównując tangens z innymi funkcjami trygonometrycznymi, można zauważyć, że tangens ma bardziej skomplikowaną strukturę, ponieważ jego wartości mogą dążyć do nieskończoności w pobliżu asymptot. To sprawia, że jego analiza jest bardziej złożona, ale również bardziej interesująca.
Związek tangensa z innymi funkcjami trygonometrycznymi
Tangens jest ściśle związany z dwiema innymi podstawowymi funkcjami trygonometrycznymi: sinus i cosinus. Można go zdefiniować jako iloraz sinusa i cosinusa danego kąta, co zapisuje się matematycznie jako: $$\text{tg}\alpha = \frac{\sin\alpha}{\cos\alpha}$$. Ta relacja pokazuje, że wartości tangensa są bezpośrednio powiązane z wartościami sinusa i cosinusa, co czyni tangens funkcją pochodną tych dwóch podstawowych funkcji.
Warto również zauważyć, że tangens jest funkcją okresową, a jego okres wynosi $$\pi$$ radianów. Oznacza to, że wartości tangensa powtarzają się co $$\pi$$ radianów, co jest istotne w analizach matematycznych i fizycznych. Ponadto, ponieważ tangens jest zdefiniowany jako stosunek, jego wartości mogą dążyć do nieskończoności, gdy cosinus wynosi zero, co prowadzi do asymptot w wykresie funkcji tangensa.
Jak tangens wpływa na zjawiska fizyczne w codziennym życiu?
Tangens odgrywa kluczową rolę w wielu zjawiskach fizycznych, które obserwujemy na co dzień. Jego zastosowanie w analizie ruchu, obliczeniach optycznych oraz w inżynierii sprawia, że jest niezbędnym narzędziem dla naukowców i inżynierów. Dzięki tangensowi możemy dokładnie obliczać kąty i wysokości obiektów, co jest nieocenione w różnych dziedzinach, takich jak geodezja czy mechanika.
- W geodezji tangens jest używany do wyznaczania wysokości obiektów na podstawie pomiaru kątów i odległości.
- W analizie ruchu pochyłego tangens pomaga określić kąt nachylenia, co jest kluczowe w obliczeniach trajektorii.
- W optyce tangens jest stosowany w obliczeniach związanych z kątami padania i odbicia światła.
Przykłady zastosowania tangensa w analizie ruchu
Tangens jest niezwykle przydatny w analizie ruchu, zwłaszcza w kontekście pochyłych płaszczyzn oraz ruchu pocisków. Na przykład, gdy analizujemy ruch obiektu zjeżdżającego po pochyłej płaszczyźnie, możemy wykorzystać tangens do obliczenia kąta nachylenia. Jeśli mamy pochyłość o długości 5 metrów i wysokości 3 metrów, kąt nachylenia można obliczyć jako $$\alpha = \text{tg}^{-1}\left(\frac{3}{5}\right)$$, co daje kąt około 30,96°. Dzięki temu możemy dokładniej określić siły działające na obiekt.
Inny przykład to analiza ruchu pocisków. Kiedy obiekt jest wyrzucany pod kątem, tangens pomaga nam określić maksymalną wysokość, jaką osiągnie. Jeśli pocisk zostanie wystrzelony z prędkością 20 m/s pod kątem 45°, możemy obliczyć wysokość, korzystając z wzoru $$h = \frac{v^2 \cdot \sin^2(\alpha)}{2g}$$, gdzie $$g$$ to przyspieszenie ziemskie. W tym przypadku, tangens odgrywa kluczową rolę w określaniu kątów i trajektorii ruchu.
| Scenariusz | Kąt nachylenia (stopnie) | Wysokość (m) | Długość (m) |
| Pochyła płaszczyzna | 30,96 | 3 | 5 |
| Ruch pocisku | 45 | 20 | 20 |
Czytaj więcej: Izotop w fizyce – co to jest i jakie ma znaczenie dla nauki?
Dlaczego znajomość tangensa jest ważna w naukach przyrodniczych?
Zrozumienie tangensa ma kluczowe znaczenie w naukach przyrodniczych, w szczególności w fizyce i inżynierii. Tangens, jako jedna z podstawowych funkcji trygonometrycznych, pozwala na analizowanie i rozwiązywanie złożonych problemów związanych z kątami, siłami i ruchami. Dzięki niemu naukowcy i inżynierowie mogą precyzyjnie obliczać wartości, które są niezbędne do prawidłowego funkcjonowania systemów mechanicznych i strukturalnych. W kontekście nauk przyrodniczych, tangens ułatwia interpretację zjawisk fizycznych oraz wspiera rozwój technologii i innowacji.
Wielu inżynierów korzysta z tangensa przy projektowaniu różnych struktur, takich jak mosty czy budynki, gdzie precyzyjne obliczenia kątów są kluczowe dla bezpieczeństwa i stabilności. Ponadto, w fizyce, tangens jest używany do analizy ruchu ciał, co pozwala na lepsze zrozumienie dynamiki i interakcji między obiektami. W ten sposób, znajomość tangensa nie tylko wspiera teoretyczne aspekty nauki, ale również ma praktyczne zastosowanie w codziennym życiu.
Tangens w kontekście sił i momentów w mechanice
Tangens odgrywa istotną rolę w analizie sił i momentów w mechanice, gdzie jest używany do obliczania kątów oraz rozkładu sił działających na obiekty. Na przykład, w przypadku układów równowagi, tangens pozwala określić, jakie siły muszą być zastosowane, aby zrównoważyć inne siły działające na dany obiekt. Gdy analizujemy siłę działającą na pochyłą płaszczyznę, tangens kąta nachylenia pozwala na obliczenie komponentów siły, co jest kluczowe dla zrozumienia ruchu obiektu.
W praktyce, inżynierowie wykorzystują tangens do obliczeń związanych z momentami sił, co jest istotne w konstrukcji maszyn i urządzeń. Na przykład, przy projektowaniu dźwigów, znajomość tangensa pozwala na określenie, jakie obciążenia mogą być przenoszone w różnych kątach. W ten sposób, tangens jest nie tylko teoretycznym narzędziem, ale również praktycznym rozwiązaniem w codziennych wyzwaniach inżynieryjnych.
Użyteczność tangensa w rozwiązywaniu problemów inżynieryjnych
Tangens jest niezwykle przydatny w inżynierii, gdzie pomaga rozwiązywać różnorodne problemy związane z analizą strukturalną i projektowaniem. Inżynierowie często wykorzystują tangens do obliczeń kątów oraz sił działających na różne elementy konstrukcyjne. Na przykład, przy projektowaniu mostów, znajomość tangensa pozwala na określenie kątów nachylenia belek, co jest kluczowe dla zapewnienia stabilności i bezpieczeństwa budowli. Dodatkowo, tangens jest używany w obliczeniach związanych z momentami sił, co ma znaczenie w konstrukcji maszyn i urządzeń.
W przypadku systemów dźwigowych, tangens jest stosowany do określenia, jakie obciążenia mogą być przenoszone w różnych kątowych ustawieniach dźwigu. Umożliwia to inżynierom optymalizację projektów i zwiększenie efektywności operacji. W ten sposób, tangens nie tylko wspiera teoretyczne aspekty inżynierii, ale również ma praktyczne zastosowanie w codziennych wyzwaniach.
- Analiza kątów nachylenia w konstrukcjach mostów, co pozwala na obliczenie sił działających na belki.
- Obliczenia w systemach dźwigowych, gdzie tangens pomaga określić maksymalne obciążenia w różnych ustawieniach.
- Projektowanie maszyn, w których tangens jest używany do analizy momentów sił działających na elementy konstrukcyjne.
Jak wykorzystać tangens w nowoczesnych technologiach inżynieryjnych?
W miarę jak technologia się rozwija, tangens staje się coraz bardziej istotny w nowoczesnych zastosowaniach, takich jak symulacje komputerowe i modelowanie 3D. Inżynierowie używają tangensa do obliczeń w programach CAD (Computer-Aided Design), co umożliwia precyzyjne projektowanie skomplikowanych struktur oraz elementów mechanicznych. Dzięki zastosowaniu tangensa w algorytmach obliczeniowych, możliwe jest szybkie i efektywne przekształcanie kątów oraz sił na modele trójwymiarowe, co znacznie ułatwia analizę i optymalizację projektów.
Co więcej, w kontekście inteligentnych systemów budowlanych i robotyki, tangens odgrywa kluczową rolę w programowaniu ruchu robotów oraz w automatyzacji procesów budowlanych. Dzięki algorytmom opartym na tangensie, roboty mogą dokładniej obliczać trajektorie ruchu, co zwiększa ich precyzję i efektywność w wykonywaniu zadań. W przyszłości, integracja tangensa z technologią sztucznej inteligencji może prowadzić do jeszcze bardziej zaawansowanych rozwiązań inżynieryjnych, które będą w stanie dostosowywać się do zmieniających się warunków pracy oraz optymalizować procesy w czasie rzeczywistym.