Symetria w matematyce to fascynujący temat, który odgrywa kluczową rolę w zrozumieniu wielu aspektów tej dziedziny. W uproszczeniu, symetria oznacza, że dany obiekt jest niezmienny w wyniku określonych przekształceń. To zjawisko można zaobserwować w różnych figurach, bryłach oraz ogólnych obiektach matematycznych. W matematyce wyróżniamy różne rodzaje symetrii, które mają zastosowanie w wielu dziedzinach nauki i życia codziennego.
W artykule przyjrzymy się definicji symetrii, jej znaczeniu oraz różnym typom, takim jak symetria odbiciowa, obrotowa i translacyjna. Zrozumienie tych pojęć pozwala nie tylko na lepsze zrozumienie matematyki, ale także na dostrzeganie symetrii w otaczającym nas świecie.
Kluczowe informacje:
- Symetria w matematyce to właściwość obiektów, które pozostają niezmienne podczas przekształceń.
- Rodzaje symetrii obejmują symetrię odbiciową, obrotową i translacyjną.
- Symetria jest istotna w matematyce, ponieważ pomaga w rozwiązywaniu problemów i zrozumieniu struktur matematycznych.
- Przykłady symetrii można znaleźć w geometrii, algebrze oraz w codziennych obiektach i zjawiskach.
Definicja symetrii w matematyce i jej znaczenie dla nauki
Symetria w matematyce to właściwość obiektów, która oznacza, że istnieje przekształcenie, które odwzorowuje dany obiekt na niego samego. Oznacza to, że obiekt pozostaje niezmienny pod wpływem tego przekształcenia. W matematyce, symetria jest kluczowym konceptem, który znajduje zastosowanie w różnych dziedzinach nauki, takich jak geometria, algebra czy fizyka. Brak symetrii w obiektach nazywany jest asymetrią, co wskazuje na ich złożoność i różnorodność.
Definicja symetrii jest istotna nie tylko w kontekście matematycznym, ale także w praktycznych zastosowaniach. Symetria pomaga w zrozumieniu struktur i wzorców, które są obecne w naturze oraz w codziennym życiu. W wielu przypadkach, zrozumienie symetrii pozwala na uproszczenie problemów matematycznych oraz na lepsze modelowanie zjawisk przyrodniczych.
Czym jest symetria w kontekście matematycznym?
W kontekście matematycznym, symetria odnosi się do właściwości figur i obiektów, które pozostają niezmienne podczas różnych przekształceń. Przykłady takich przekształceń to odbicie, obrót czy translacja. Symetria może występować w różnych formach, co sprawia, że jest to ważny temat w matematyce. W różnych kontekstach, symetria może oznaczać coś innego, ale zawsze odnosi się do niezmienności obiektów w wyniku określonych działań.
Symetria jest również kluczowym pojęciem w teorii grup, która bada struktury matematyczne. W tej teorii, symetrie są reprezentowane jako operacje, które mogą być stosowane do obiektów, co pozwala na ich analizę i klasyfikację. Dzięki temu, matematycy mogą lepiej zrozumieć, jak różne obiekty są ze sobą powiązane.
Dlaczego symetria jest ważna w matematyce i naukach ścisłych?
Symetria odgrywa kluczową rolę w matematyce, ponieważ ułatwia rozwiązywanie problemów i zrozumienie skomplikowanych struktur. Dzięki symetrii, matematycy mogą dostrzegać wzorce, które pomagają w analizie i klasyfikacji obiektów matematycznych. W naukach ścisłych, takich jak fizyka czy chemia, symetria jest niezbędna do formułowania teorii i modeli, które opisują zachowanie materii i energii w różnych systemach.
Symetria nie tylko upraszcza obliczenia, ale również pozwala na przewidywanie wyników eksperymentów. W wielu przypadkach, symetria prowadzi do odkryć, które zmieniają nasze rozumienie świata. Dlatego jej znaczenie wykracza poza matematykę i obejmuje różne dziedziny nauki, podkreślając jej uniwersalny charakter.
Rodzaje symetrii w matematyce i ich zastosowania
W matematyce wyróżniamy kilka rodzajów symetrii, które mają swoje specyficzne zastosowania. Najpopularniejsze z nich to symetria odbiciowa, obrotowa oraz translacyjna. Każdy z tych typów symetrii ma swoje unikalne cechy i zastosowania, które są istotne w różnych dziedzinach, takich jak geometria, algebra czy sztuka. Zrozumienie tych rodzajów symetrii jest kluczowe dla analizy obiektów matematycznych i ich właściwości.
Symetria odbiciowa, na przykład, jest często obserwowana w naturze, w formach takich jak skrzydła motyli. Symetria obrotowa znajduje zastosowanie w architekturze oraz projektowaniu, gdzie obiekty są projektowane z myślą o estetyce i funkcjonalności. Z kolei symetria translacyjna jest szeroko stosowana w teorii grup oraz w analizie wzorów i struktur.
Symetria odbiciowa: zrozumienie i przykłady
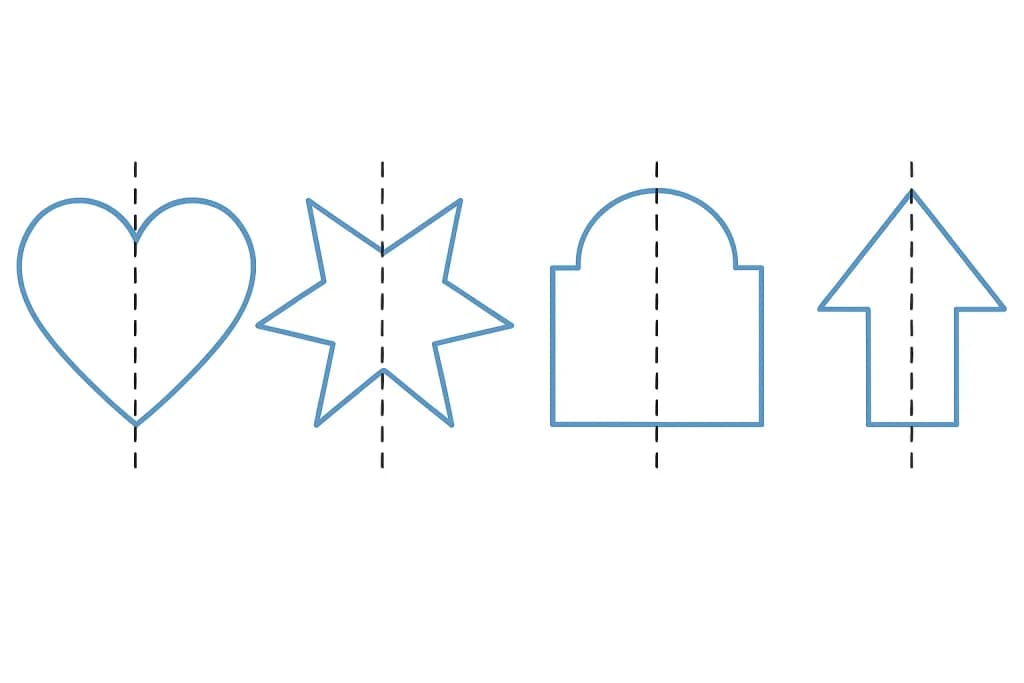
Symetria odbiciowa, znana również jako symetria lustrzana, to zjawisko, w którym obiekt jest niezmienny pod względem kształtu i rozmiaru po odbiciu w linii (osi symetrii). Oznacza to, że jedna połowa obiektu jest dokładnym odwzorowaniem drugiej. Przykłady symetrii odbiciowej można znaleźć w naturze, jak na przykład w skrzydłach motyli, które mają identyczne wzory po obu stronach ciała, co sprawia, że są one doskonałym przykładem tego typu symetrii.
Inne przykłady symetrii odbiciowej obejmują ludzką twarz, gdzie prawa i lewa strona są w dużej mierze symetryczne, oraz niektóre architektoniczne elementy budynków, takie jak okna czy drzwi, które są zaprojektowane w taki sposób, aby tworzyć harmonijną całość. Symetria odbiciowa jest również często wykorzystywana w sztuce i projektowaniu, gdzie estetyka opiera się na równowadze i harmonii.
- Skrzydła motyli, które mają identyczne wzory po obu stronach.
- Tworzenie wzorów na tkaninach, które są symetryczne wzdłuż osi.
- Wzory na niektórych budynkach, które wykorzystują symetrię odbiciową w swoim projekcie.
Symetria obrotowa: jak działa i gdzie ją znaleźć?
Symetria obrotowa występuje, gdy obiekt wygląda tak samo po obrocie o pewien kąt wokół punktu centralnego. Inaczej mówiąc, obiekt ma symetrię obrotową, jeśli można go obrócić o określoną ilość stopni i uzyskać ten sam wygląd. Przykłady symetrii obrotowej można znaleźć w kwiatach, takich jak stokrotki, które mają wiele płatków rozmieszczonych równomiernie wokół centralnego punktu, co sprawia, że wyglądają identycznie po obrocie.
Innym przykładem są koła, które mają nieskończoną ilość symetrii obrotowej, ponieważ można je obracać w dowolnym kierunku bez zmiany ich kształtu. Symetria obrotowa jest również obecna w niektórych elementach architektonicznych, jak np. w wieżach czy kolumnach, które są projektowane z myślą o estetyce i funkcjonalności.
| Obiekt | Kąt obrotu (stopnie) |
| Stokrotka | 360° (przy 30°) |
| Koło | 360° (dowolny kąt) |
| Wieża | 90° (przy 90°) |
Symetria translacyjna: zastosowanie w różnych dziedzinach
Symetria translacyjna to zjawisko, w którym obiekt jest przesuwany w określonym kierunku, a jego wygląd pozostaje niezmieniony. Przykłady symetrii translacyjnej można znaleźć w wielu dziedzinach, takich jak sztuka, architektura czy matematyka. Na przykład, wzory na płytkach ceramicznych często wykorzystują translacyjną symetrię, aby stworzyć powtarzające się motywy, które są estetycznie przyjemne. Kolejnym przykładem są tkaniny, gdzie wzory są projektowane w taki sposób, aby były symetryczne wzdłuż osi przesunięcia.
W architekturze, translacyjna symetria jest wykorzystywana w projektowaniu elewacji budynków, gdzie okna i drzwi są rozmieszczone w regularny sposób, tworząc harmonijny wygląd. W matematyce, translacyjna symetria jest istotna w analizie wzorów i struktur, ponieważ pozwala na zrozumienie, jak różne elementy są ze sobą powiązane w przestrzeni.
Czytaj więcej: Rodzaje diagramów w matematyce – poznaj ich zastosowanie i przykłady

Przykłady symetrii w matematyce i ich praktyczne znaczenie
Symetria w matematyce ma wiele praktycznych zastosowań, które są kluczowe w różnych dziedzinach. Na przykład, w geometrii, symetria pozwala na uproszczenie obliczeń oraz lepsze zrozumienie właściwości figur. Przykłady symetrii można znaleźć w algebrze, gdzie równania z symetrycznymi właściwościami ułatwiają ich rozwiązanie. Analizując te przykłady, matematycy mogą dostrzegać wzorce, które prowadzą do odkryć i nowych teorii.
Symetria odgrywa również istotną rolę w naukach przyrodniczych, gdzie pomaga w modelowaniu zjawisk oraz w przeprowadzaniu eksperymentów. Na przykład, w fizyce, symetria jest kluczowa dla zrozumienia zachowań cząstek subatomowych. W ten sposób, symetria nie tylko ułatwia rozwiązywanie problemów matematycznych, ale także wpływa na nasze zrozumienie świata i jego zjawisk.
Symetria w geometrii: figury i ich właściwości
Symetria odgrywa kluczową rolę w geometrii, gdzie wiele figur wykazuje swoje unikalne właściwości dzięki symetrii. Na przykład, kwadrat ma cztery osie symetrii, co oznacza, że można go podzielić na równe części wzdłuż tych osi. Podobnie, koło ma nieskończoną liczbę osi symetrii, ponieważ każda linia przechodząca przez jego środek dzieli je na dwie identyczne części. Takie właściwości symetrii są nie tylko estetyczne, ale również praktyczne, ponieważ ułatwiają obliczenia i analizę.
Inne figury, takie jak trójkąt równoboczny, również wykazują symetrię, mając trzy osie symetrii. Symetria w geometrii pomaga w zrozumieniu, jak różne figury są ze sobą powiązane oraz jakie mają właściwości. Dzięki tym właściwościom, matematycy mogą tworzyć bardziej złożone struktury i modele, co jest kluczowe w wielu zastosowaniach, od architektury po inżynierię.
Symetria w algebrze: równania i ich rozwiązania
W algebrze, symetria odnosi się do równań, które mają pewne właściwości symetryczne. Na przykład, równanie x^2 + y^2 = r^2 jest symetryczne względem osi X i Y, co oznacza, że jego wykres wygląda tak samo, niezależnie od tego, czy przesuniemy go w górę, w dół, w lewo czy w prawo. Tego typu symetria jest istotna, ponieważ pozwala na łatwiejsze rozwiązywanie równań oraz przewidywanie ich zachowań.
Innym przykładem może być równanie x^3 - 3xy^2 = 0, które również wykazuje symetrię, ponieważ można je przekształcić na różne sposoby, zachowując jego formę. Symetria w algebrze pomaga matematykom zrozumieć, jak różne zmienne wpływają na siebie, co jest kluczowe w analizie funkcji i rozwiązywaniu złożonych problemów matematycznych.
Jak wykorzystać symetrię w projektowaniu i sztuce współczesnej
Symetria nie tylko odgrywa kluczową rolę w matematyce, ale ma również ogromne znaczenie w projektowaniu i sztuce współczesnej. Wykorzystanie symetrii w architekturze może prowadzić do tworzenia harmonijnych i estetycznie przyjemnych przestrzeni. Przykładowo, wiele nowoczesnych budynków, takich jak muzeum Guggenheima w Bilbao, wykorzystuje zasady symetrii, aby przyciągnąć wzrok i stworzyć unikalne doświadczenia dla odwiedzających. Projektanci często stosują symetrię, aby wprowadzić równowagę i proporcje, co sprzyja lepszemu odbiorowi wizualnemu.
W sztuce, artyści mogą stosować symetrię w kompozycji, aby prowadzić spojrzenie widza przez dzieło. Zastosowanie symetrii odbiciowej lub obrotowej w malarstwie czy rzeźbie może wzmacniać przekaz emocjonalny i narracyjny. W dobie cyfrowej, narzędzia do projektowania graficznego umożliwiają artystom eksperymentowanie z symetrią w sposób, który wcześniej był trudny do osiągnięcia, co otwiera nowe możliwości twórcze i innowacyjne podejścia do tradycyjnych form sztuki.