Figury geometryczne przestrzenne to trójwymiarowe kształty, które mają długość, szerokość i wysokość. W przeciwieństwie do figur płaskich, bryły geometryczne są bardziej złożone. Występują w różnych formach, takich jak graniastosłupy, ostrosłupy, bryły obrotowe i sześciany. Każda z tych figur ma swoje unikalne właściwości, w tym objętość i pole powierzchni. Figury przestrzenne są ważne w wielu dziedzinach, od architektury po sztukę.
Najważniejsze informacje:- Figury przestrzenne mają trzy wymiary: długość, szerokość i wysokość
- Główne typy to graniastosłupy, ostrosłupy, bryły obrotowe i sześciany
- Każda figura ma swoją objętość i pole powierzchni
- Stosowane są w architekturze, inżynierii i sztuce
- Zrozumienie figur przestrzennych pomaga lepiej pojmować otaczający świat
Czym są figury geometryczne przestrzenne?
Figury geometryczne przestrzenne, zwane również bryłami geometrycznymi, to kształty trójwymiarowe posiadające długość, szerokość i wysokość. W przeciwieństwie do figur płaskich, formy przestrzenne zajmują określoną objętość. Figury 3D odgrywają kluczową rolę w matematyce, szczególnie w dziedzinie stereometrii. W życiu codziennym otaczają nas na każdym kroku, od pudełek po skomplikowane konstrukcje architektoniczne.
Podstawowe rodzaje figur przestrzennych
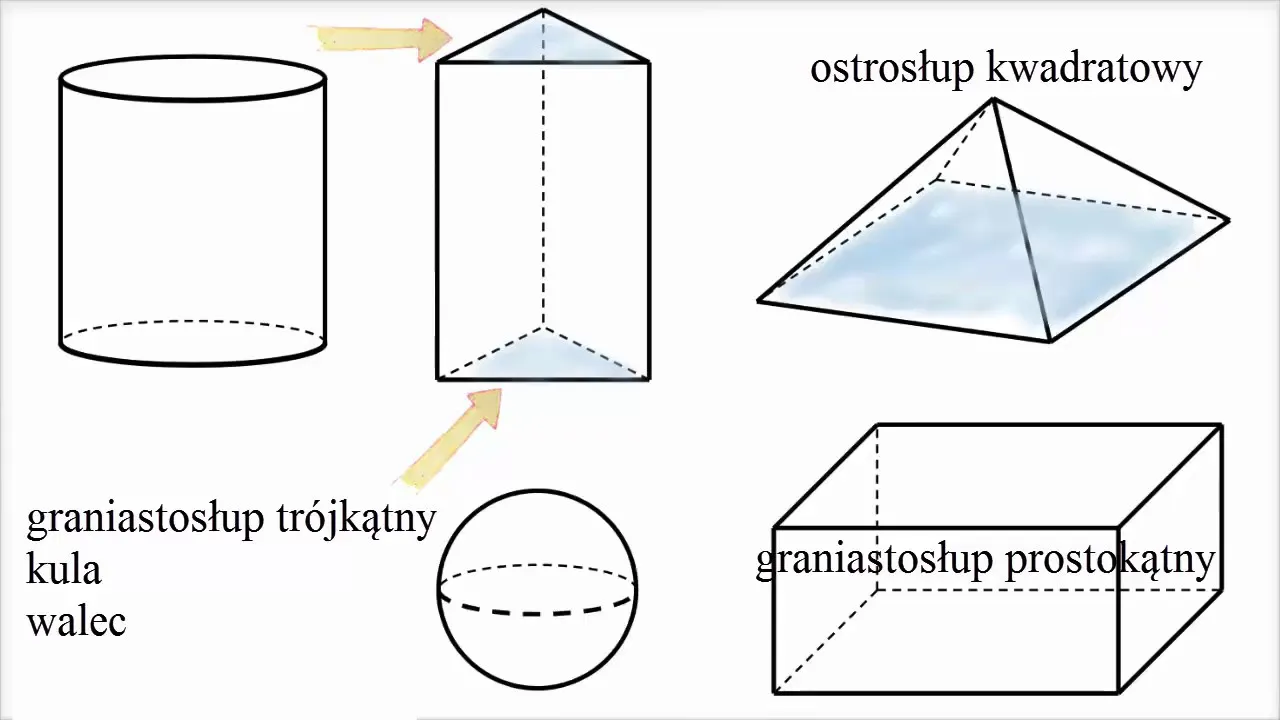
Graniastosłupy
Graniastosłupy to bryły geometryczne z dwiema równoległymi, identycznymi podstawami i prostokątnymi ścianami bocznymi. Ich kształt zależy od rodzaju wielokąta tworzącego podstawę.
- Prostopadłościan
- Sześcian
- Graniastosłup trójkątny
Ostrosłupy
Ostrosłupy to figury geometryczne przestrzenne składające się z podstawy (wielokąta) i trójkątnych ścian bocznych zbiegających się w jednym punkcie - wierzchołku. Ich nazwa często pochodzi od kształtu podstawy.
- Ostrosłup czworokątny
- Ostrosłup trójkątny
- Piramida (ostrosłup o podstawie kwadratu)
Bryły obrotowe
Bryły obrotowe powstają przez obrót figury płaskiej wokół prostej (osi obrotu). Ten proces tworzy symetryczne obiekty geometryczne przestrzenne.
- Walec
- Stożek
- Kula
Kluczowe właściwości figur przestrzennych
Objętość
Objętość to ilość przestrzeni zajmowanej przez bryłę geometryczną. W praktyce pozwala określić pojemność zbiorników czy wielkość budynków.
| Figura | Wzór na objętość |
|---|---|
| Prostopadłościan | V = a * b * h |
| Kula | V = 4/3 * π * r³ |
| Stożek | V = 1/3 * π * r² * h |
Pole powierzchni
Pole powierzchni to suma pól wszystkich ścian figury przestrzennej. Ma kluczowe znaczenie przy obliczaniu ilości materiału potrzebnego do pokrycia bryły.
| Figura | Wzór na pole powierzchni |
|---|---|
| Sześcian | P = 6 * a² |
| Walec | P = 2 * π * r * (r + h) |
| Ostrosłup prawidłowy czworokątny | P = a² + 2 * a * s |
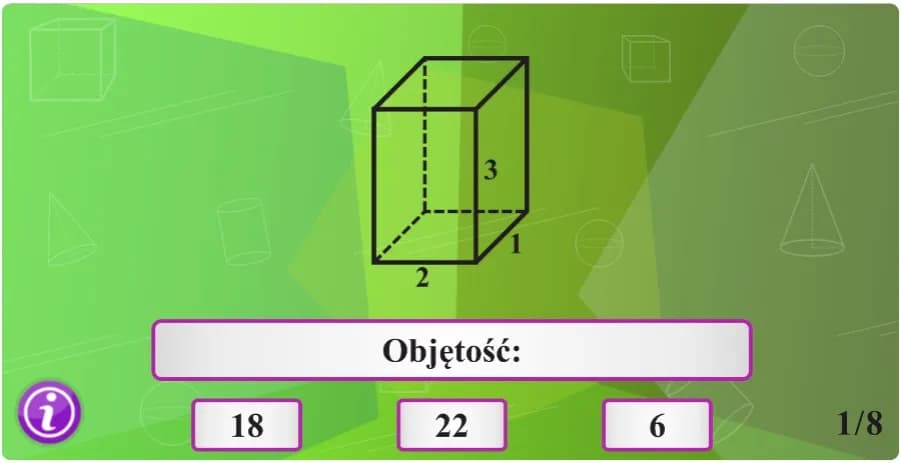
Jak obliczyć objętość i pole powierzchni figur przestrzennych?
Obliczanie wymiarów brył geometrycznych wymaga znajomości odpowiednich wzorów i danych wejściowych. Kluczowe jest zrozumienie relacji między elementami figury. Weźmy na przykład walec. Aby obliczyć jego objętość, mnożymy pole podstawy przez wysokość: V = π * r² * h. Dla walca o promieniu 3 cm i wysokości 5 cm, objętość wyniesie około 141,37 cm³.
Zastosowania figur geometrycznych przestrzennych
W architekturze
Kształty trójwymiarowe są fundamentem projektowania budynków. Architekci wykorzystują różnorodne bryły geometryczne, aby tworzyć funkcjonalne i estetyczne konstrukcje. Przykładem jest piramida Luwru w Paryżu, łącząca formę ostrosłupa ze szklaną fasadą.
W inżynierii
Inżynierowie regularnie pracują z figurami przestrzennymi przy projektowaniu maszyn i konstrukcji. Znajomość właściwości brył pozwala optymalizować wytrzymałość i wydajność. Dobrym przykładem jest konstrukcja mostów, gdzie zastosowanie odpowiednich kształtów wpływa na ich nośność.
W sztuce
Artyści często wykorzystują formy przestrzenne do tworzenia rzeźb i instalacji. Obiekty geometryczne przestrzenne pozwalają na eksperymentowanie z formą i perspektywą. Sztuka kubistyczna Pabla Picassa to doskonały przykład wykorzystania geometrii w malarstwie.
Dlaczego warto znać figury geometryczne przestrzenne?
Znajomość brył geometrycznych wspiera rozwój myślenia matematycznego i przestrzennego. Ułatwia rozwiązywanie problemów nie tylko w szkole, ale i w codziennym życiu. W praktyce, umiejętność rozpoznawania i analizy figur 3D przydaje się przy pakowaniu walizki czy organizacji przestrzeni w domu. Regularne obcowanie z kształtami trójwymiarowymi znacząco poprawia naszą percepcję przestrzenną, co jest cenną umiejętnością w wielu dziedzinach życia i kariery.
Figury przestrzenne: klucz do zrozumienia otaczającego nas świata
Figury geometryczne przestrzenne to fascynujący temat, który wykracza daleko poza szkolne ławki. Od prostych graniastosłupów po skomplikowane bryły obrotowe, te trójwymiarowe kształty są fundamentem naszego otoczenia. Zrozumienie ich właściwości, takich jak objętość i pole powierzchni, otwiera drzwi do wielu dziedzin - od architektury po inżynierię.
Praktyczne zastosowania brył geometrycznych spotykamy na każdym kroku. Architekci wykorzystują je do projektowania budynków, inżynierowie do tworzenia mostów, a artyści do wyrażania swoich wizji. Nawet w codziennym życiu, umiejętność rozpoznawania i analizy figur 3D może okazać się niezwykle przydatna.
Zgłębianie tematu form przestrzennych to nie tylko nauka wzorów i definicji. To rozwój umiejętności przestrzennych, kreatywnego myślenia i zdolności rozwiązywania problemów. Dlatego warto poświęcić czas na poznanie tych fascynujących kształtów - to inwestycja, która zaprocentuje w wielu aspektach naszego życia.