Aby wyznaczyć równanie okręgu, kluczowe jest zrozumienie jego podstawowych elementów, takich jak środek i promień. Równanie okręgu w postaci kanonicznej, które ma formę (x - a)² + (y - b)² = r², pozwala na łatwe odczytanie współrzędnych środka oraz długości promienia. Wiedza na temat tych parametrów jest niezbędna do prawidłowego określenia równania w różnych sytuacjach, takich jak gdy znamy punkty leżące na okręgu lub gdy potrzebujemy przekształcić równanie z formy ogólnej.
W artykule przedstawimy różne metody wyznaczania równania okręgu, w tym obliczanie promienia z danych punktów oraz przekształcanie równania z postaci ogólnej do kanonicznej. Dzięki tym informacjom, czytelnik będzie mógł samodzielnie wyznaczać równania okręgów w różnych kontekstach matematycznych.
Najistotniejsze informacje:- Równanie okręgu w postaci kanonicznej to (x - a)² + (y - b)² = r², gdzie (a, b) to współrzędne środka, a r to promień.
- Promień można obliczyć jako odległość między środkiem okręgu a punktem na jego obwodzie.
- Jeśli znane są dwa punkty na okręgu oraz dodatkowy warunek, można wykorzystać równość odległości, aby znaleźć środek okręgu.
- Równanie okręgu w postaci ogólnej można przekształcić do postaci kanonicznej, co ułatwia jego analizę.
- W przypadku okręgu stycznego do osi układu współrzędnych, odległość środka od osi jest równa promieniowi.
Jak wyznaczyć równanie okręgu - podstawowe pojęcia i definicje
Równanie okręgu jest kluczowym elementem w geometrii analitycznej. Aby wyznaczyć równanie okręgu, należy zrozumieć jego podstawowe składniki, takie jak środek i promień. Okrąg to zbiór punktów w płaszczyźnie, które są w równej odległości od ustalonego punktu, nazywanego środkiem okręgu. Współrzędne tego punktu oznaczamy jako (a, b), a odległość, czyli promień, oznaczamy jako r. Te elementy są niezbędne do sformułowania równania okręgu.
Równanie okręgu w postaci kanonicznej ma postać (x - a)² + (y - b)² = r². Z tego równania można łatwo odczytać zarówno położenie środka, jak i długość promienia. Warto zauważyć, że znajomość tych parametrów umożliwia nam dalsze analizy i obliczenia związane z okręgiem. W kolejnych częściach artykułu omówimy metody wyznaczania równania okręgu oraz przekształcanie równań z formy ogólnej do kanonicznej.
Zrozumienie okręgu: definicja, środek i promień
Okrąg można zdefiniować jako zbiór punktów w płaszczyźnie, które są oddalone od określonego punktu, nazywanego środkiem, o stałą odległość, czyli promień. Środek okręgu to punkt, którego współrzędne zapisujemy jako (a, b), a promień to odległość od środka do dowolnego punktu na obwodzie okręgu. Te dwa elementy są kluczowe dla zrozumienia i wyznaczenia równania okręgu, ponieważ na ich podstawie możemy określić kształt i położenie okręgu w układzie współrzędnych.
Równanie okręgu w formie kanonicznej - co to oznacza?
Równanie okręgu w formie kanonicznej jest jednym z najważniejszych sposobów przedstawienia okręgu w matematyce. Ma ono postać (x - a)² + (y - b)² = r², gdzie (a, b) to współrzędne środka, a r to długość promienia. Ta forma równania jest szczególnie przydatna, ponieważ pozwala na szybkie zidentyfikowanie kluczowych parametrów okręgu. Dzięki temu, mając dane wartości a, b i r, możemy łatwo zbudować pełne równanie okręgu i wykorzystać je w dalszych obliczeniach.
Metody wyznaczania równania okręgu z danych punktów
W celu wyznaczenia równania okręgu, istnieje kilka metod, które można zastosować, w zależności od dostępnych danych. Gdy znamy środek okręgu oraz jego promień, możemy łatwo skonstruować równanie w postaci kanonicznej. W przypadku, gdy posiadamy dwa punkty leżące na okręgu, możemy wykorzystać różne techniki do określenia równania, uwzględniając dodatkowe warunki, takie jak położenie środka w danym układzie współrzędnych. Każda z tych metod ma swoje zastosowanie i pozwala na uzyskanie precyzyjnych wyników.
Jednym z najprostszych sposobów na wyznaczenie równania okręgu jest posiadanie współrzędnych jego środka oraz długości promienia. W takim przypadku wystarczy podstawić te wartości do równania kanonicznego (x - a)² + (y - b)² = r². Jeśli natomiast mamy dwa punkty na obwodzie okręgu, możemy obliczyć środek jako punkt równoodległy od tych punktów, a następnie obliczyć promień jako odległość od środka do jednego z tych punktów. To podejście pozwala na uzyskanie równania okręgu bez znajomości jego bezpośrednich parametrów.
Wyznaczanie równania z podanego środka i promienia
Aby znaleźć równanie okręgu na podstawie środka i promienia, należy najpierw zidentyfikować współrzędne środka, które oznaczamy jako (a, b), oraz wartość promienia r. W przypadku, gdy te dane są dostępne, równanie okręgu można sformułować w postaci kanonicznej jako (x - a)² + (y - b)² = r². Ta forma równania jest bardzo wygodna, ponieważ od razu pokazuje, gdzie znajduje się środek oraz jak duży jest okrąg.
- Środek okręgu to punkt o współrzędnych (a, b).
- Promień r to stała odległość od środka do dowolnego punktu na obwodzie okręgu.
- Równanie kanoniczne można łatwo przekształcić do formy ogólnej, jeśli zajdzie taka potrzeba.
Jak znaleźć równanie okręgu z punktów leżących na okręgu?
Aby wyznaczyć równanie okręgu z punktów leżących na jego obwodzie, potrzebujemy co najmniej trzech punktów, które nie są współliniowe. Pierwszym krokiem jest zidentyfikowanie współrzędnych tych punktów, które oznaczymy jako (x_1, y_1), (x_2, y_2) oraz (x_3, y_3). Następnie, możemy skorzystać z układu równań, który pozwoli nam obliczyć środek okręgu oraz jego promień. W tym celu wykorzystujemy fakt, że środek okręgu jest równoodległy od wszystkich punktów na jego obwodzie.
Możemy również skorzystać z metody współrzędnych środkowych, aby znaleźć środek okręgu. Po obliczeniu współrzędnych środka, promień można obliczyć jako odległość między środkiem a jednym z punktów. Na koniec, mając te wartości, możemy sformułować równanie w postaci kanonicznej. Ta metoda jest szczególnie przydatna, gdy nie mamy bezpośrednich danych o środku i promieniu, a jedynie punkty na obwodzie okręgu.
- Punkt A: (2, 3)
- Punkt B: (4, 7)
- Punkt C: (6, 5)
Przekształcanie równania kanonicznego do formy ogólnej
Aby przekształcić równanie okręgu z formy kanonicznej do formy ogólnej, należy zacząć od równania kanonicznego, które ma postać (x - a)² + (y - b)² = r², gdzie (a, b) to współrzędne środka okręgu, a r to promień. Pierwszym krokiem jest rozwinięcie kwadratów, co daje: x² - 2ax + a² + y² - 2by + b² = r². Następnie, przekształcamy to równanie, przenosząc wszystkie składniki na jedną stronę, co prowadzi do postaci: x² + y² - 2ax - 2by + (a² + b² - r²) = 0. W ten sposób uzyskujemy równanie okręgu w formie ogólnej, które można wykorzystać w dalszych analizach.
Jak interpretować równanie ogólne okręgu?
Równanie ogólne okręgu ma postać x² + y² - 2ax - 2by + c = 0, gdzie a i b są współrzędnymi środka okręgu, a c jest stałą, która wpływa na położenie okręgu w układzie współrzędnych. Wartości -2a i -2b wskazują, jak daleko od początku układu współrzędnych znajduje się środek okręgu. Promień okręgu można obliczyć z wyrażenia r = √(a² + b² - c). Dzięki tej interpretacji, równanie ogólne staje się użyteczne w analizie geometrycznej oraz przy przekształcaniu do formy kanonicznej.
Czytaj więcej: Jak pozbyć się pierwiastka z równania i uniknąć typowych błędów
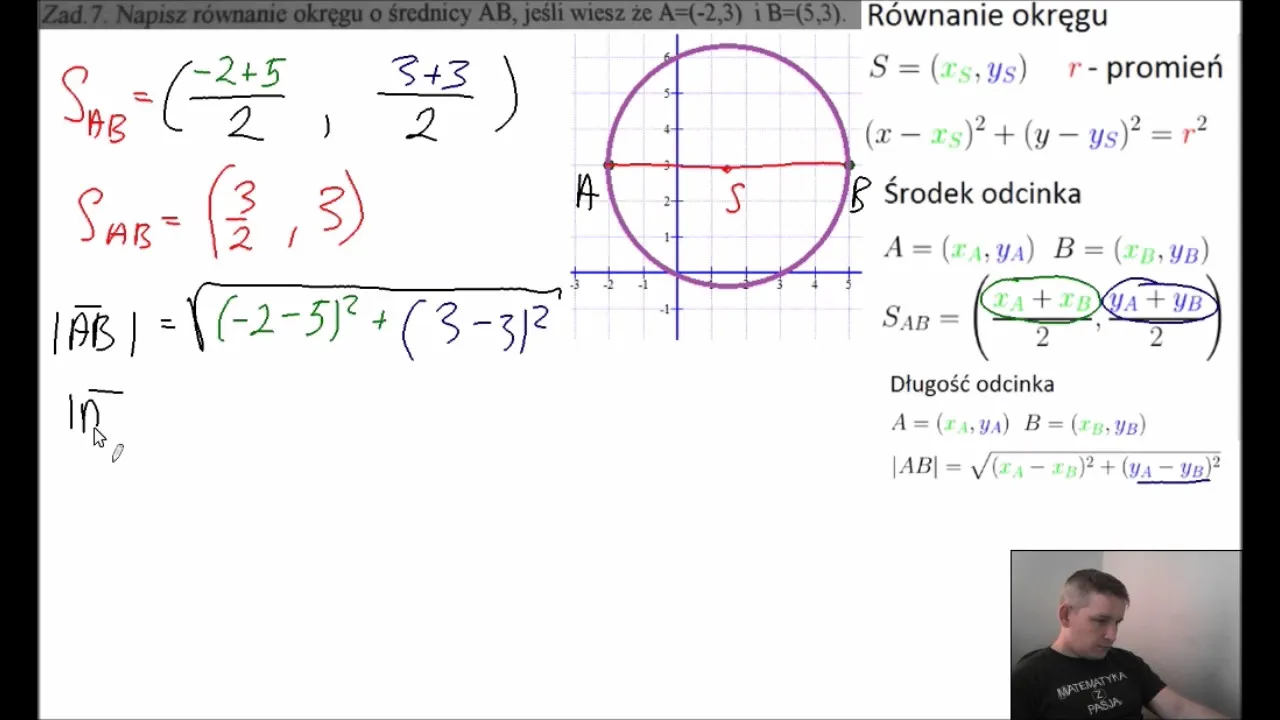
Przykłady krok po kroku - zastosowanie teorii w praktyce
W praktyce, aby wyznaczyć równanie okręgu, można zastosować różne metody, które omówiliśmy wcześniej. W tej sekcji przedstawimy dwa konkretne przykłady, które ilustrują, jak można wykorzystać te metody do uzyskania równania okręgu. Przykłady te pomogą lepiej zrozumieć, w jaki sposób można przełożyć teoretyczne zasady na konkretne obliczenia, co jest niezwykle przydatne w matematyce i geometrii analitycznej.
W pierwszym przykładzie wyznaczymy równanie okręgu na podstawie trzech punktów leżących na jego obwodzie. W drugim przykładzie, mamy dane współrzędne środka oraz promień okręgu, co pozwoli nam na szybkie skonstruowanie równania w postaci kanonicznej. Te dwa przypadki pokazują, jak różne dane mogą prowadzić do tego samego celu – określenia równania okręgu w układzie współrzędnych.
Przykład 1: Równanie okręgu z danymi punktami
Aby znaleźć równanie okręgu z punktów leżących na jego obwodzie, weźmy pod uwagę trzy punkty: A(2, 3), B(4, 7) oraz C(6, 5). Pierwszym krokiem jest obliczenie współrzędnych środka okręgu. Możemy to zrobić, korzystając z metody równoodległości. Następnie, obliczamy promień jako odległość od środka do jednego z punktów. Po uzyskaniu tych wartości, podstawiamy je do równania kanonicznego (x - a)² + (y - b)² = r², co pozwala nam uzyskać pełne równanie okręgu.
| Punkt | Współrzędne |
|---|---|
| A | (2, 3) |
| B | (4, 7) |
| C | (6, 5) |
Przykład 2: Równanie okręgu z określonym środkiem i promieniem
W tym przykładzie mamy dany środek okręgu S(3, 2) oraz promień r = 5. Aby wyznaczyć równanie okręgu, podstawiamy te wartości do równania kanonicznego. Otrzymujemy równanie (x - 3)² + (y - 2)² = 5², co po przekształceniu daje (x - 3)² + (y - 2)² = 25. To równanie jasno pokazuje, gdzie znajduje się okrąg oraz jaką ma średnicę. Warto upewnić się, że obliczenia są poprawne, a wartości są zgodne z danymi wyjściowymi.
Praktyczne zastosowania równań okręgów w inżynierii i grafice
Równania okręgów mają szerokie zastosowanie w różnych dziedzinach, takich jak inżynieria, architektura oraz grafika komputerowa. W inżynierii, na przykład, równania okręgów są kluczowe przy projektowaniu elementów maszyn, takich jak koła zębate czy wały. Dzięki precyzyjnemu określeniu parametrów okręgu, inżynierowie mogą zapewnić, że elementy te będą działały z odpowiednią dokładnością i efektywnością. W grafice komputerowej, równania okręgów są wykorzystywane do modelowania obiektów oraz animacji, co pozwala na tworzenie bardziej realistycznych wizualizacji.
W przyszłości, z rozwojem technologii druku 3D oraz symulacji komputerowych, umiejętność efektywnego korzystania z równań okręgów stanie się jeszcze bardziej istotna. Inżynierowie i projektanci będą musieli być biegli w przekształcaniu równań matematycznych w fizyczne obiekty, co wymaga zrozumienia zarówno teorii, jak i praktycznych zastosowań. Warto zatem rozwijać swoje umiejętności w tej dziedzinie, aby móc w pełni wykorzystać możliwości, jakie oferują nowoczesne technologie.
