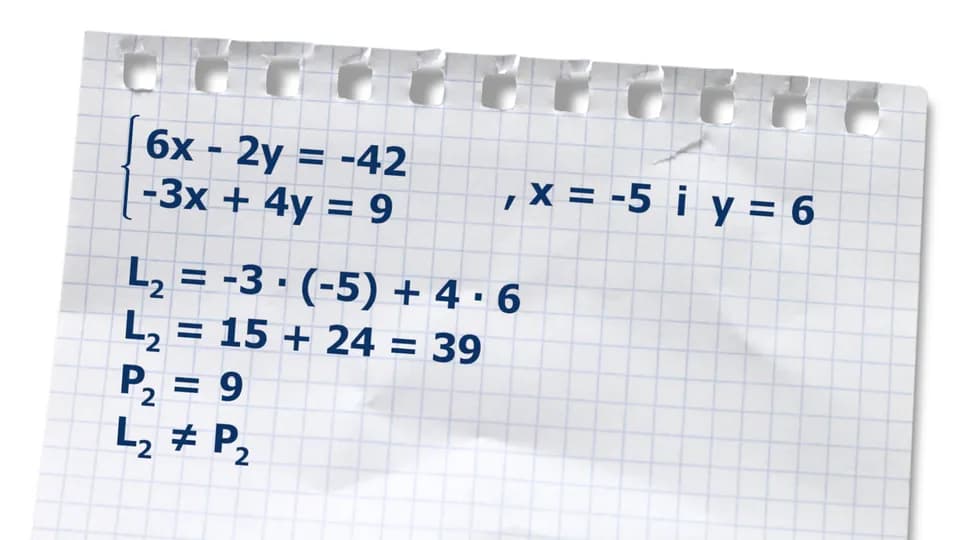Rozwiązywanie układu równań z dwiema niewiadomymi to kluczowa umiejętność w matematyce, która znajduje zastosowanie w wielu dziedzinach, od nauk ścisłych po ekonomię. Istnieje kilka metod, które można wykorzystać do rozwiązania takich układów, w tym metoda podstawiania, metoda przeciwnych współczynników oraz metoda wyznaczników. W tym artykule przedstawimy te metody, aby pomóc Ci zrozumieć, jak skutecznie rozwiązywać układy równań.
Każda z metod ma swoje zalety i jest użyteczna w różnych sytuacjach. Na przykład, metoda podstawiania jest idealna, gdy jedno z równań można łatwo przekształcić, aby wyizolować jedną niewiadomą. Z kolei metoda przeciwnych współczynników może być szybsza, gdy oba równania są już w odpowiedniej formie. Zrozumienie tych technik pozwoli Ci na swobodne poruszanie się w świecie równań i ich rozwiązywania.
Kluczowe informacje:- Układ równań z dwiema niewiadomymi można rozwiązać za pomocą różnych metod, takich jak podstawianie, przeciwnych współczynników i wyznaczniki.
- Metoda podstawiania polega na wyizolowaniu jednej niewiadomej i podstawieniu jej wartości do drugiego równania.
- Metoda przeciwnych współczynników polega na manipulacji równaniami, aby wyeliminować jedną z niewiadomych.
- Wyznaczniki to matematyczne narzędzie, które można wykorzystać do rozwiązywania układów równań, szczególnie w przypadku większych systemów.
- Ważne jest, aby znać typowe błędy, które mogą wystąpić podczas rozwiązywania układów równań, aby ich unikać.
Jak rozwiązać układ równań z 2 niewiadomymi – podstawowe metody
Rozwiązywanie układu równań z dwiema niewiadomymi jest kluczowym elementem matematyki, który ma zastosowanie w różnych dziedzinach, takich jak fizyka, ekonomia czy inżynieria. Istnieje kilka metod, które można wykorzystać, aby skutecznie znaleźć rozwiązania, a dwie z najpopularniejszych to metoda podstawiania oraz metoda przeciwnych współczynników. Obie techniki pozwalają na wyznaczenie wartości niewiadomych w układzie równań, co jest niezbędne do dalszych obliczeń.
Metoda podstawiania polega na wyizolowaniu jednej z niewiadomych w jednym z równań i podstawieniu jej wartości do drugiego równania. Z kolei metoda przeciwnych współczynników skupia się na manipulacji równaniami w taki sposób, aby jedna z niewiadomych została wyeliminowana. W każdej z tych metod kluczowe jest zrozumienie, jak przekształcać równania, aby uzyskać poprawne wyniki.
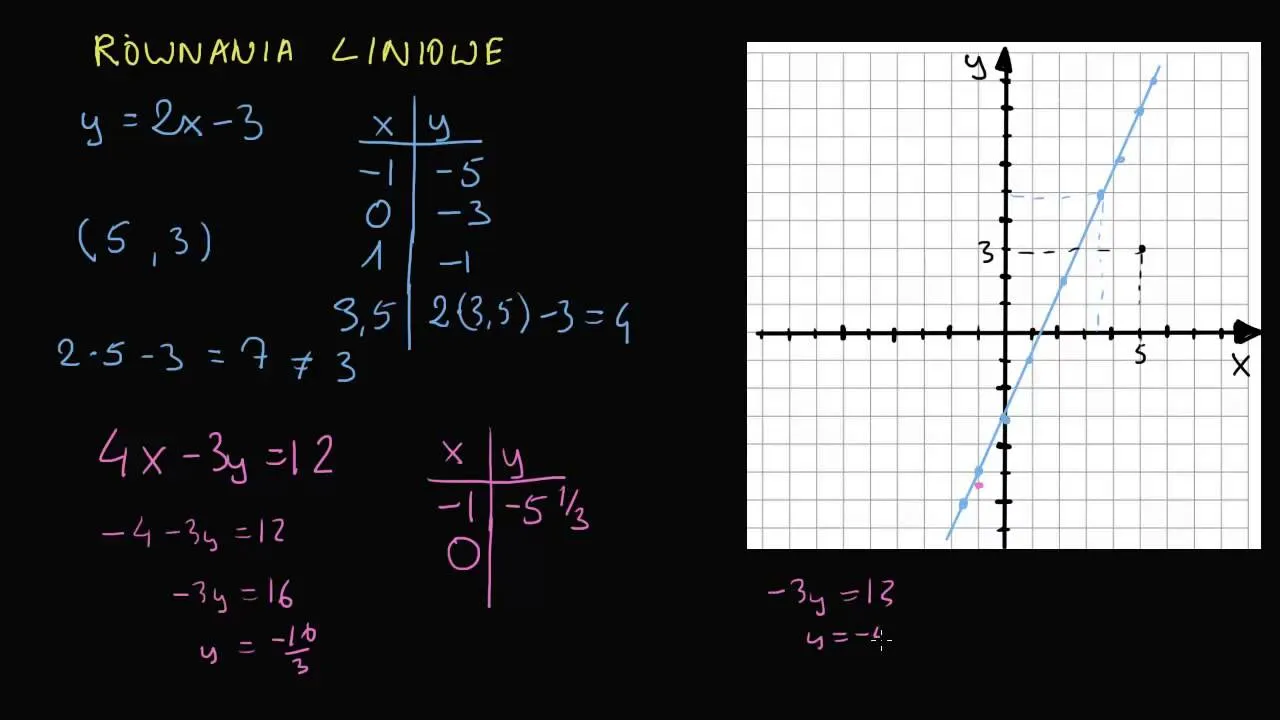
Metoda podstawiania – krok po kroku do rozwiązania równań
Metoda podstawiania to jedna z najprostszych technik rozwiązywania układów równań. Aby ją zastosować, należy najpierw wyizolować jedną z niewiadomych w jednym z równań. Na przykład, jeśli mamy równanie 2x + y = 10, możemy wyznaczyć y jako y = 10 - 2x. Następnie tę wartość podstawiamy do drugiego równania, co pozwala nam znaleźć wartość drugiej niewiadomej.
Oto krok po kroku, jak przeprowadzić metodę podstawiania:
- Wybierz równanie, w którym łatwiej jest wyizolować jedną z niewiadomych.
- Wyizoluj niewiadomą i zapisz ją w postaci zależności od drugiej niewiadomej.
- Podstaw tę wartość do drugiego równania.
- Rozwiąż nowe równanie, aby znaleźć wartość drugiej niewiadomej.
- Podstaw otrzymaną wartość z powrotem do równania, aby znaleźć wartość pierwszej niewiadomej.
Metoda przeciwnych współczynników – szybkie i efektywne rozwiązanie
Metoda przeciwnych współczynników to kolejna popularna technika rozwiązywania układów równań z dwiema niewiadomymi. Jej głównym celem jest eliminacja jednej z niewiadomych poprzez dodawanie lub odejmowanie równań. Dzięki temu można szybko znaleźć wartość drugiej niewiadomej, co czyni tę metodę bardzo efektywną w wielu sytuacjach. Jest szczególnie przydatna, gdy równania są już w odpowiedniej formie, co pozwala na łatwą manipulację.
Proces eliminacji polega na przekształceniu równań w taki sposób, aby jedna z niewiadomych zniknęła. Na przykład, jeśli mamy układ równań, możemy pomnożyć jedno z równań przez odpowiedni współczynnik, aby uzyskać równe współczynniki przy jednej z niewiadomych. Następnie dodajemy lub odejmujemy równania, co pozwala na uproszczenie układu do jednego równania z jedną niewiadomą. Po znalezieniu wartości tej niewiadomej, możemy wrócić do pierwotnych równań, aby wyznaczyć drugą niewiadomą.
| Metoda podstawiania | Metoda przeciwnych współczynników |
| Łatwa do zrozumienia i stosunkowo prosta w użyciu. | Szybsza w przypadku dobrze dopasowanych równań. |
| Może być bardziej czasochłonna w przypadku złożonych równań. | Wymaga przekształcenia równań, co może być trudne dla niektórych użytkowników. |
| Idealna do równań o prostych współczynnikach. | Skuteczna w przypadku równań z większymi współczynnikami. |
Zrozumienie wyznaczników i ich zastosowanie w równaniach
Wyznaczniki to kluczowy element w matematyce, szczególnie w kontekście rozwiązywania układów równań. Są one liczbami, które można przypisać do macierzy i które dostarczają informacji o jej właściwościach. Wyznacznik można obliczyć dla macierzy kwadratowej, a jego wartość ma istotne znaczenie w kontekście rozwiązania układów równań. Na przykład, jeśli wyznacznik macierzy jest różny od zera, oznacza to, że układ równań ma jedno unikalne rozwiązanie.
Obliczanie wyznaczników jest ważne, ponieważ pozwala na szybkie określenie, czy dane równania można rozwiązać. W praktyce, wyznaczniki są używane w różnych metodach, takich jak metoda Cramera, która wykorzystuje je do znajdowania wartości niewiadomych w układach równań. Zrozumienie, jak obliczać wyznaczniki oraz znać ich zastosowanie, jest niezbędne dla każdego, kto chce efektywnie rozwiązywać układy równań z dwiema niewiadomymi.
Przykład zastosowania wyznaczników w układzie równań
Rozważmy układ równań, który można rozwiązać za pomocą wyznaczników:
- Równanie 1: 2x + 3y = 5
- Równanie 2: 4x - y = 7
Aby zastosować wyznaczniki, najpierw zapisujemy układ równań w formie macierzy. Następnie obliczamy wyznacznik macierzy współczynników. W tym przypadku macierz współczynników to:
| 2 | 3 |
| 4 | -1 |
Obliczamy wyznacznik tej macierzy, co pozwala nam stwierdzić, czy układ ma rozwiązanie. Po obliczeniu wyznacznika, możemy również użyć metod takich jak metoda Cramera, aby znaleźć wartości x i y. To podejście jest szczególnie przydatne w bardziej złożonych układach, gdzie inne metody mogą być mniej efektywne.
Typowe błędy przy rozwiązywaniu układów równań i jak ich unikać
Rozwiązywanie układów równań z dwiema niewiadomymi może być skomplikowane, a popełnianie błędów jest powszechne, zwłaszcza w przypadku metod takich jak podstawianie i eliminacja. Rozpoznawanie tych błędów jest kluczowe, aby uniknąć fałszywych wyników i frustracji podczas rozwiązywania równań. Wiele osób może nieświadomie popełniać błędy, które prowadzą do błędnych interpretacji lub niepoprawnych odpowiedzi. Dlatego warto znać najczęstsze pułapki, aby móc je skutecznie unikać.
Najczęstsze pułapki w metodzie podstawiania i eliminacji
W przypadku metody podstawiania, jednym z najczęstszych błędów jest niewłaściwe przekształcenie równania. Na przykład, jeśli zapomnisz zmienić znaku przy przenoszeniu terminu z jednej strony równania na drugą, możesz uzyskać błędne wartości niewiadomych. Innym problemem jest niepoprawne podstawienie wartości do drugiego równania, co prowadzi do całkowicie nieprawidłowego rozwiązania. Aby uniknąć tych błędów, zawsze sprawdzaj swoje obliczenia i upewnij się, że każde przekształcenie jest wykonane poprawnie.
W metodzie przeciwnych współczynników, najczęstsze pułapki obejmują błędne mnożenie równań przez współczynniki, co może prowadzić do błędnych wartości. Często zdarza się także, że użytkownicy mylą znaki przy dodawaniu lub odejmowaniu równań, co skutkuje nieprawidłowymi wynikami. Aby tego uniknąć, warto dokładnie przeanalizować każdy krok, upewniając się, że wszystkie operacje są poprawne.
Jak poprawnie interpretować wyniki rozwiązań równań
Interpretacja wyników uzyskanych z układów równań jest kluczowym krokiem w procesie rozwiązywania. Po znalezieniu wartości niewiadomych, ważne jest, aby zrozumieć, co te wyniki oznaczają w kontekście problemu. Istnieją trzy główne typy rozwiązań: jedno rozwiązanie, nieskończona liczba rozwiązań oraz brak rozwiązania. Każdy z tych przypadków wymaga innego podejścia do analizy i weryfikacji.
Aby zweryfikować uzyskane rozwiązania, można podstawić wartości niewiadomych z powrotem do oryginalnych równań. Jeśli równania są spełnione, oznacza to, że rozwiązanie jest poprawne. W przypadku, gdy równania nie są spełnione, warto sprawdzić, czy popełniono jakieś błędy w obliczeniach. Ponadto, w przypadku układów z nieskończoną liczbą rozwiązań, ważne jest, aby zrozumieć, że równania są ze sobą powiązane i można je przedstawić w innej formie.
Czytaj więcej: Koszty nauczania domowego: Od zera do kilku tysięcy złotych
Jak wykorzystać układy równań w rzeczywistych problemach codziennych
Układy równań z dwiema niewiadomymi mają szerokie zastosowanie w codziennym życiu, zwłaszcza w dziedzinach takich jak ekonomia, inżynieria czy nauki przyrodnicze. Przykładowo, można je wykorzystać do modelowania sytuacji związanych z budżetem domowym, gdzie równania mogą reprezentować różne wydatki i przychody. Dzięki umiejętności rozwiązywania takich układów, można podejmować lepsze decyzje finansowe, analizując, jak zmiany w jednym z wydatków wpływają na ogólną sytuację finansową.
Innym praktycznym zastosowaniem jest optymalizacja procesów produkcyjnych w przemyśle. Firmy często korzystają z układów równań do określenia, ile surowców powinny zamówić, aby zaspokoić popyt na swoje produkty przy minimalnych kosztach. W miarę jak technologia się rozwija, umiejętność modelowania i rozwiązywania układów równań będzie coraz bardziej cenna, zwłaszcza w kontekście analizy danych i sztucznej inteligencji, gdzie te techniki są podstawą wielu algorytmów. Umożliwia to nie tylko efektywne zarządzanie zasobami, ale także przewidywanie przyszłych trendów rynkowych.
