Równania kwadratowe to kluczowy temat w matematyce, który pojawia się w różnych dziedzinach nauki i codziennego życia. Ich ogólna postać to ax² + bx + c = 0, gdzie a, b i c to współczynniki liczbowe. Rozwiązywanie takich równań może wydawać się skomplikowane, ale istnieje kilka prostych metod, które umożliwiają znalezienie ich rozwiązań. W artykule omówimy różne techniki, takie jak faktoryzacja, użycie wzoru kwadratowego oraz metoda dopełniania kwadratu.
Każda z tych metod ma swoje zastosowanie w zależności od konkretnego równania. Dzięki zrozumieniu, jak obliczać deltę, możemy łatwo określić liczbę rozwiązań danego równania. Warto wiedzieć, że jeśli delta jest większa od zera, równanie ma dwa rozwiązania, jeśli równa się zeru - jedno, a jeśli jest mniejsza od zera, nie ma rozwiązań w zbiorze liczb rzeczywistych. Poznanie tych podstawowych zasad pozwoli na skuteczne rozwiązywanie równań kwadratowych w praktyce.
Kluczowe informacje:- Równania kwadratowe mają postać ax² + bx + c = 0, gdzie a, b i c są współczynnikami.
- Delta obliczana jest jako Δ = b² - 4ac, co pozwala ocenić liczbę rozwiązań.
- Jeśli Δ > 0, równanie ma dwa rozwiązania, które można obliczyć za pomocą wzorów x₁ = (-b - √Δ) / 2a oraz x₂ = (-b + √Δ) / 2a.
- Gdy Δ = 0, istnieje jedno rozwiązanie x = -b / 2a.
- W przypadku Δ < 0, równanie nie ma rozwiązań w liczbach rzeczywistych.
Jak rozwiązywać równania kwadratowe - przegląd metod i technik
Równania kwadratowe to istotny element matematyki, który można rozwiązać na różne sposoby. Wśród najpopularniejszych metod znajdują się spierwiastkowanie obustronne, korzystanie ze wzorów skróconego mnożenia, wyciąganie wspólnego czynnika przed nawias oraz stosowanie wzoru na deltę. Każda z tych technik ma swoje zastosowanie i może być użyta w zależności od konkretnego równania.
Aby skutecznie rozwiązać równanie kwadratowe, należy najpierw sprowadzić je do postaci ogólnej ax² + bx + c = 0, gdzie a, b i c to współczynniki liczbowe. Następnie kluczowym krokiem jest obliczenie delty, która jest definiowana jako Δ = b² - 4ac. Wartość delty pozwala określić liczbę rozwiązań równania oraz ich charakter.
Zrozumienie równania kwadratowego - definicja i elementy
Równanie kwadratowe to równanie, w którym najwyższa potęga zmiennej x jest równa 2. Oznacza to, że w równaniu występuje składnik kwadratowy, co czyni je różnym od równań liniowych. W standardowej postaci równania kwadratowego ax² + bx + c = 0, współczynnik a nie może być równy zeru, ponieważ w przeciwnym razie równanie przestaje być kwadratowe.
Współczynniki a, b i c mają różne znaczenie. Współczynnik a określa, jak "wąskie" lub "szerokie" jest parabola, którą reprezentuje równanie. Wartość b wpływa na położenie wierzchołka paraboli, a c to punkt przecięcia paraboli z osią y. Zrozumienie tych elementów jest kluczowe dla skutecznego rozwiązywania równań kwadratowych.
Rozwiązywanie równania kwadratowego metodą faktoryzacji - krok po kroku
Faktoryzacja to jedna z najprostszych metod rozwiązywania równań kwadratowych. Polega ona na przekształceniu równania do postaci iloczynowej, co umożliwia łatwe znalezienie pierwiastków. Aby skutecznie zastosować tę metodę, należy najpierw upewnić się, że równanie ma postać ax² + bx + c = 0, a następnie znaleźć takie liczby, które spełniają warunki równania.
Krok po kroku, proces faktoryzacji można opisać w kilku etapach. Pierwszym krokiem jest wyciągnięcie wspólnego czynnika, jeśli to możliwe. Następnie szukamy dwóch liczb, które mnożąc się dają ac (iloczyn współczynnika a i c) oraz sumują się do b. Gdy te liczby są znalezione, możemy zapisać równanie w postaci iloczynowej i łatwo obliczyć pierwiastki.
- Wyciągnij wspólny czynnik, jeśli to możliwe.
- Znajdź liczby, które mnożą się do ac i sumują do b.
- Przekształć równanie do postaci iloczynowej.
- Rozwiąż równanie, ustawiając każdy czynnik równy zero.
Użycie wzoru kwadratowego - jak go zastosować w praktyce
Wzór kwadratowy to uniwersalne narzędzie do rozwiązywania równań kwadratowych. Umożliwia on znalezienie pierwiastków równania w sposób systematyczny, niezależnie od tego, czy równanie jest łatwe do faktoryzacji. Wzór ten ma postać: x = (-b ± √Δ) / 2a, gdzie Δ to delta, obliczana jako Δ = b² - 4ac.
Aby zastosować wzór kwadratowy, najpierw obliczamy deltę. Następnie, w zależności od wartości delty, możemy określić liczbę rozwiązań równania. Jeśli Δ > 0, otrzymujemy dwa różne pierwiastki. Gdy Δ = 0, mamy jedno rozwiązanie. W przypadku, gdy Δ < 0, równanie nie ma rozwiązań w zbiorze liczb rzeczywistych.
| Wartość delty (Δ) | Liczba rozwiązań | Rodzaj rozwiązań |
| Δ > 0 | 2 | Różne pierwiastki |
| Δ = 0 | 1 | Podwójny pierwiastek |
| Δ < 0 | 0 | Brak rozwiązań w liczbach rzeczywistych |
Metoda dopełniania kwadratu - jak skutecznie ją wykorzystać
Dopełnianie kwadratu to skuteczna metoda rozwiązywania równań kwadratowych, która polega na przekształceniu równania w taki sposób, aby umożliwić łatwe wyznaczenie pierwiastków. Dzięki tej metodzie można przekształcić równanie w postać, która pozwala na łatwe obliczenie wartości zmiennej. Proces ten opiera się na dodaniu i odjęciu odpowiedniej wartości, co umożliwia utworzenie kwadratu z binomii.
Aby zastosować metodę dopełniania kwadratu, należy najpierw sprowadzić równanie do postaci ax² + bx + c = 0. Następnie, w przypadku gdy a jest różne od 1, dzielimy całe równanie przez a. Kolejnym krokiem jest przekształcenie wyrażenia bx do postaci kwadratu. W tym celu dodajemy i odejmujemy (b/2)², co pozwala na zapisanie równania w formie (x + b/2)² = Δ, gdzie Δ to wartość obliczona z pozostałych składników równania.
- Przekształć równanie do postaci ax² + bx + c = 0.
- Jeśli a ≠ 1, podziel całe równanie przez a.
- Dodaj i odejmij (b/2)² do równania.
- Przekształć równanie do postaci (x + b/2)² = Δ.
- Oblicz pierwiastki, rozwiązując równanie kwadratowe.
Przykładowe równanie, które można rozwiązać tą metodą, to x² + 6x + 8 = 0. Po przekształceniu i dodaniu (6/2)² = 9, otrzymujemy (x + 3)² = 1, co prowadzi do rozwiązania x = -3 ± 1, czyli x₁ = -2 oraz x₂ = -4. Metoda dopełniania kwadratu jest szczególnie przydatna, gdy równania nie można łatwo faktoryzować.
Rozwiązywanie równania kwadratowego z liczbami całkowitymi - przykłady
Rozwiązywanie równań kwadratowych z liczbami całkowitymi jest często prostsze, ponieważ współczynniki są łatwiejsze do manipulacji. Przykładowe równanie, które można rozwiązać, to x² - 5x + 6 = 0. Aby znaleźć pierwiastki, możemy zastosować metodę faktoryzacji. Szukamy dwóch liczb, które mnożą się do 6 (iloczyn c) i sumują do -5 (współczynnik b). W tym przypadku są to -2 i -3.
Równanie możemy przekształcić do postaci iloczynowej: (x - 2)(x - 3) = 0. Teraz, aby znaleźć rozwiązania, ustawiamy każdy czynnik równy zero. Otrzymujemy: x - 2 = 0 oraz x - 3 = 0, co prowadzi do rozwiązań x₁ = 2 oraz x₂ = 3. To proste równanie doskonale ilustruje, jak faktoryzacja ułatwia proces rozwiązywania.
Równania kwadratowe z współczynnikami ułamkowymi - jak je rozwiązać
Równania kwadratowe z współczynnikami ułamkowymi mogą wydawać się bardziej skomplikowane, ale zasady pozostają te same. Rozważmy równanie 0.5x² - 3x + 2 = 0. Aby uprościć obliczenia, możemy najpierw pozbyć się ułamków, mnożąc całe równanie przez 2, co daje: x² - 6x + 4 = 0.
Następnie możemy użyć wzoru kwadratowego, aby znaleźć pierwiastki. Obliczamy deltę: Δ = (-6)² - 4 * 1 * 4 = 36 - 16 = 20. Teraz możemy zastosować wzór kwadratowy: x = (6 ± √20) / 2. Po uproszczeniu uzyskujemy dwa rozwiązania: x₁ = 3 + √5 oraz x₂ = 3 - √5. Te ułamkowe współczynniki pokazują, że metoda kwadratowa jest niezawodna, niezależnie od rodzaju współczynników.
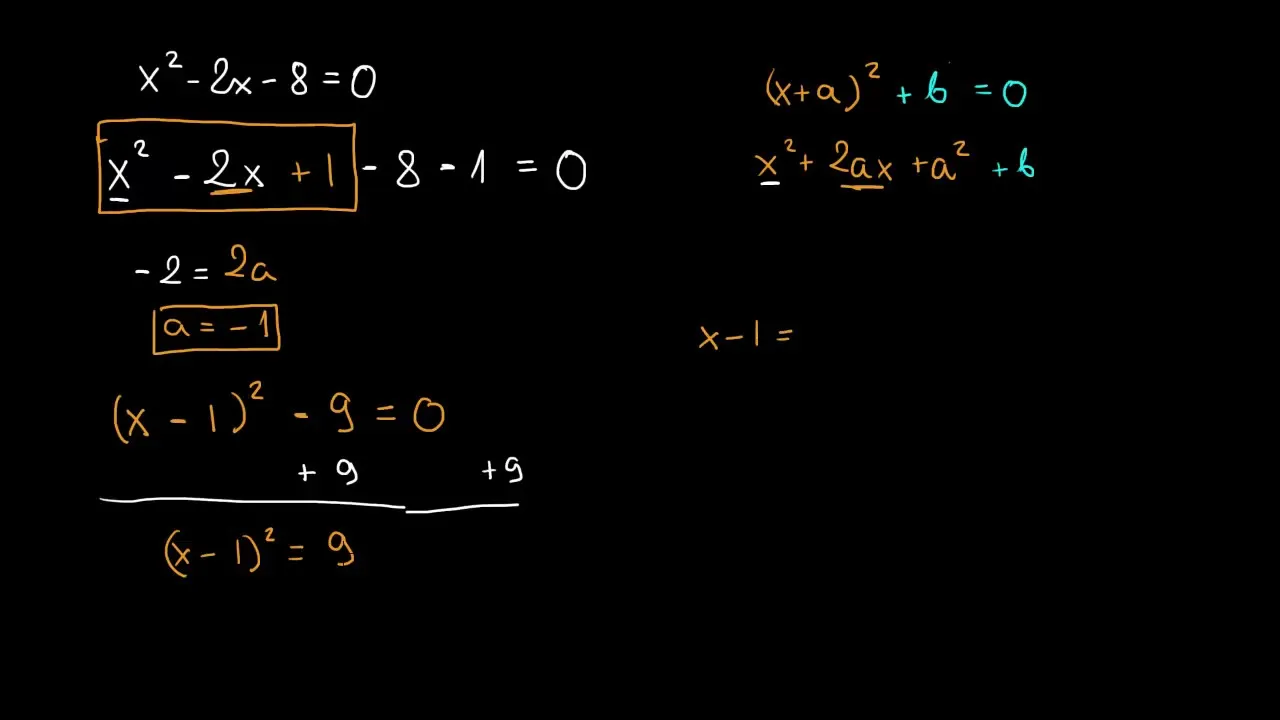
Typowe błędy przy rozwiązywaniu równań kwadratowych - co unikać
Podczas rozwiązywania równań kwadratowych, wiele osób popełnia typowe błędy, które mogą prowadzić do nieprawidłowych wyników. Często zdarza się, że uczniowie mylą wzory lub nieprawidłowo obliczają deltę. Zrozumienie najczęstszych pułapek jest kluczowe dla skutecznego rozwiązywania równań kwadratowych i uniknięcia frustracji.
Innym powszechnym błędem jest pomijanie jednego z rozwiązań, zwłaszcza gdy delta jest większa od zera. Uczniowie często koncentrują się na jednym pierwiastku, co prowadzi do niepełnych odpowiedzi. Ważne jest, aby zawsze sprawdzić, czy obliczone wartości są poprawne i czy spełniają pierwotne równanie.
Najczęstsze pułapki w faktoryzacji - jak ich nie popełniać
Faktoryzacja równań kwadratowych to metoda, która może być prosta, ale zawiera wiele pułapek. Jednym z najczęstszych błędów jest niewłaściwe rozpoznanie liczb, które mnożą się do ac i sumują do b. Uczniowie mogą pomylić znaki lub wartości, co prowadzi do błędnych wyników. Ważne jest, aby dokładnie sprawdzić, czy wybrane liczby są poprawne.
Innym problemem jest nieuwzględnienie wspólnego czynnika, jeśli taki istnieje. Często uczniowie zapominają, że można uprościć równanie przed przystąpieniem do faktoryzacji. Dlatego zawsze warto zacząć od sprawdzenia, czy równanie można uprościć, co może znacznie ułatwić dalsze obliczenia.
Problemy z zastosowaniem wzoru kwadratowego - co może pójść nie tak
Podczas korzystania ze wzoru kwadratowego, wiele osób napotyka na trudności związane z obliczaniem delty. Często zdarza się, że uczniowie mylą znaki lub pomijają ważne elementy wzoru, co prowadzi do błędnych wyników. Należy pamiętać, że delta musi być obliczona dokładnie, aby uzyskać prawidłowe rozwiązania.
Innym typowym problemem jest nieprawidłowe stosowanie wzoru kwadratowego w przypadku, gdy delta jest mniejsza od zera. W takich sytuacjach uczniowie mogą próbować znaleźć pierwiastki, mimo że równanie nie ma rozwiązań w zbiorze liczb rzeczywistych. Ważne jest, aby zrozumieć, że w takich przypadkach należy po prostu stwierdzić, że równanie nie ma rozwiązań.
Czytaj więcej: Rzemieślnicza Zasadnicza Szkoła Zawodowa im. S. Palucha: Edukacja z pasją
Praktyczne zastosowania równań kwadratowych w technologii
Równania kwadratowe mają szerokie zastosowanie nie tylko w matematyce, ale także w różnych dziedzinach technologii i inżynierii. Na przykład, w inżynierii oprogramowania, algorytmy optymalizacji często wykorzystują równania kwadratowe do modelowania kosztów i wydajności. Dzięki temu inżynierowie mogą tworzyć bardziej efektywne systemy, które minimalizują zużycie zasobów, co jest kluczowe w projektowaniu nowoczesnych aplikacji i systemów komputerowych.
Dodatkowo, w naukach przyrodniczych, równania kwadratowe są używane do modelowania zjawisk fizycznych, takich jak trajektorie ruchu ciał w polu grawitacyjnym. Dzięki zastosowaniu równań kwadratowych, naukowcy mogą przewidywać ruchy planet, co jest niezbędne w astronomii i eksploracji kosmosu. W miarę rozwoju technologii, umiejętność rozwiązywania równań kwadratowych staje się coraz bardziej istotna, zwłaszcza w kontekście analizy danych i modelowania matematycznego.
