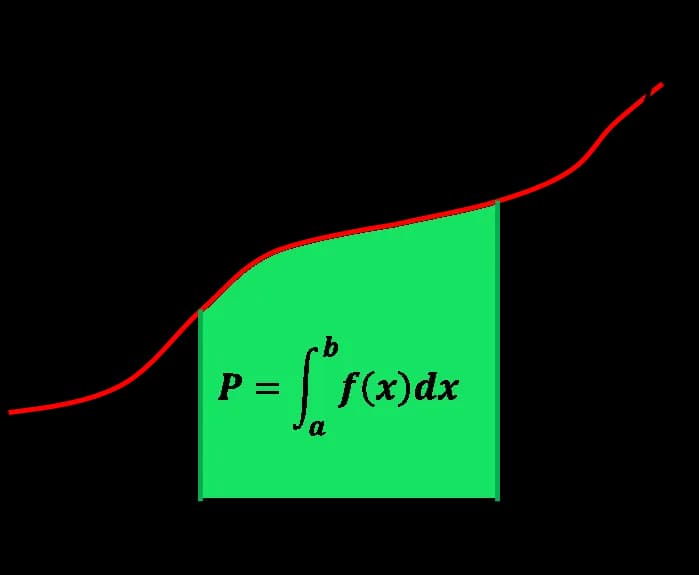
W matematyce terminy "całka oznaczona" i "całka nieoznaczona" odgrywają kluczową rolę w analizie funkcji i obliczeniach. Całka oznaczona jest definiowana na konkretnym przedziale, co pozwala na obliczenie pola pod krzywą w danym zakresie. Z kolei całka nieoznaczona jest bardziej ogólna i nie ma określonych granic, co sprawia, że jej zastosowanie jest szersze w kontekście analizy matematycznej.
W niniejszym artykule przyjrzymy się różnicom między tymi dwoma rodzajami całek. Zrozumienie tych różnic jest istotne nie tylko dla studentów matematyki, ale także dla każdego, kto chce zgłębić tajniki analizy matematycznej i zastosowań całek w różnych dziedzinach.
Kluczowe wnioski:- Całka oznaczona pozwala na obliczenie pola pod krzywą w określonym przedziale.
- Całka nieoznaczona nie ma granic, co czyni ją bardziej uniwersalną w zastosowaniach analitycznych.
- Różnice między całkami dotyczą również ich interpretacji graficznej oraz zastosowań w praktyce.
- Obie całki mają istotne znaczenie w różnych dziedzinach matematyki, takich jak fizyka i inżynieria.
- Warto znać konkretne przykłady zastosowań, aby lepiej zrozumieć te pojęcia w praktyce.
Zrozumienie całek oznaczonych i nieoznaczonych w matematyce
W matematyce całki oznaczone i nieoznaczone są fundamentalnymi pojęciami, które pomagają w analizie funkcji i obliczeniach. Całka oznaczona jest definiowana na konkretnym przedziale i pozwala na obliczenie pola pod krzywą w tym zakresie. Dzięki temu możemy zrozumieć, jak funkcja zachowuje się w danym obszarze, co jest niezwykle istotne w wielu dziedzinach, takich jak fizyka czy inżynieria. Z drugiej strony, całka nieoznaczona jest bardziej ogólnym przypadkiem, który nie ma określonych granic, co sprawia, że jej zastosowanie jest szersze w kontekście analizy matematycznej.
Oba typy całek mają swoje unikalne właściwości i zastosowania. Całki oznaczone są często używane do obliczeń praktycznych, np. w obliczaniu pól powierzchni czy objętości, podczas gdy całki nieoznaczone są kluczowe w rozwiązaniach równań różniczkowych i znajdowaniu funkcji pierwotnych. Zrozumienie różnic między tymi dwoma rodzajami całek jest kluczowe dla każdego, kto chce zgłębić tajniki matematyki i jej zastosowań w różnych dziedzinach.Definicja całki oznaczonej i jej zastosowania w praktyce
Całka oznaczona jest definiowana jako limit sumy Riemanna, która zbiega do wartości całki w miarę, jak liczba podprzedziałów dąży do nieskończoności. W praktyce oznacza to, że możemy obliczyć pole pod krzywą funkcji w danym przedziale, co jest niezwykle przydatne w wielu zastosowaniach inżynieryjnych i naukowych. Właściwości całki oznaczonej, takie jak addytywność i liniowość, sprawiają, że jest ona łatwa w użyciu w różnych kontekstach.
Przykładem zastosowania całki oznaczonej może być obliczanie pola powierzchni pod wykresem funkcji kwadratowej, takiej jak f(x) = x², w przedziale od 0 do 2. W tym przypadku, całka oznaczona pozwala na wyznaczenie pola, które wynosi 4/3. Takie obliczenia są niezbędne w inżynierii, gdzie często trzeba określić powierzchnie i objętości, a całki oznaczone dostarczają dokładnych wyników.
Definicja całki nieoznaczonej i jej znaczenie w matematyce
Całka nieoznaczona jest definiowana jako zbiór wszystkich funkcji pierwotnych danej funkcji. W matematyce, całka nieoznaczona oznaczana jest symbolem ∫f(x)dx, co wskazuje na funkcję f(x), której całkę chcemy obliczyć. Główną cechą całki nieoznaczonej jest to, że nie ma ona określonych granic, co oznacza, że wynikiem jest funkcja, a nie liczba. Właściwości całki nieoznaczonej obejmują liniowość oraz to, że różniczkowanie i całkowanie są operacjami odwrotnymi.
Znaczenie całki nieoznaczonej w matematyce jest ogromne, ponieważ stanowi fundament analizy matematycznej. Umożliwia ona rozwiązanie wielu problemów, takich jak znajdowanie funkcji pierwotnych, co jest kluczowe w kontekście równań różniczkowych. Całki nieoznaczone są także wykorzystywane w różnych dziedzinach nauki, w tym w fizyce i inżynierii, gdzie pomagają w modelowaniu zjawisk naturalnych. W ten sposób, całka nieoznaczona staje się nie tylko narzędziem teoretycznym, ale także praktycznym w zastosowaniach naukowych.
Kluczowe różnice między całką oznaczoną a nieoznaczoną
Różnice między całką oznaczoną a nieoznaczoną są fundamentalne w matematyce. Całka oznaczona jest definiowana na określonym przedziale, co pozwala na obliczenie pola pod krzywą, podczas gdy całka nieoznaczona nie ma granic i prowadzi do funkcji pierwotnej. W praktyce oznacza to, że całki oznaczone mają zastosowanie w obliczeniach ilościowych, takich jak pole powierzchni, natomiast całki nieoznaczone są używane do analizy i rozwiązywania równań różniczkowych. Dodatkowo, całka oznaczona zwraca wartość liczbową, a całka nieoznaczona zwraca funkcję.Podsumowując, kluczowe różnice między tymi dwoma rodzajami całek dotyczą ich definicji, zastosowań oraz wyników. Zrozumienie tych różnic jest istotne dla każdego, kto chce zgłębić temat całek w matematyce. Wiedza ta pozwala na lepsze wykorzystanie całek w różnych dziedzinach, a także na rozwijanie umiejętności analitycznych i obliczeniowych.
Zakres i granice w całkach oznaczonych i nieoznaczonych
Zakres i granice są kluczowymi pojęciami w kontekście całek, wpływającymi na sposób, w jaki obliczamy wartości całek. W przypadku całek oznaczonych, granice definiują przedział, na którym dokonuje się obliczeń. Oznacza to, że całka oznaczona oblicza pole pod krzywą pomiędzy dwoma punktami, co jest istotne w praktycznych zastosowaniach takich jak obliczanie powierzchni czy objętości. W przeciwieństwie do tego, całki nieoznaczone nie mają określonych granic, co sprawia, że ich zakres jest nieograniczony, a wynikiem jest funkcja.
W praktyce, zrozumienie różnicy między zakresem a granicami jest istotne dla poprawności obliczeń. Granice w całkach oznaczonych pozwalają na precyzyjne określenie, w jakim zakresie funkcja jest analizowana, co jest kluczowe w wielu zastosowaniach inżynieryjnych. Z kolei całki nieoznaczone, nie mając granic, dają możliwość analizy funkcji w szerszym kontekście, co jest przydatne w rozwiązywaniu równań różniczkowych i w teorii funkcji. Dzięki tym różnicom, obie całki pełnią różne, ale równie ważne role w matematyce.
Interpretacja graficzna całek oznaczonych i nieoznaczonych
Graficzna interpretacja całek jest kluczowym narzędziem do zrozumienia ich działania. Całki oznaczone można wizualizować jako pole pod krzywą funkcji w określonym przedziale. W przypadku całek nieoznaczonych, ich graficzna reprezentacja pokazuje zbiór funkcji pierwotnych, które mogą być przesunięte wzdłuż osi y. Tego rodzaju wizualizacje pomagają w lepszym zrozumieniu, jak całki działają i jakie mają zastosowanie w różnych kontekstach matematycznych.
| Typ całki | Graficzna reprezentacja |
| Całka oznaczona | Obszar pod krzywą na określonym przedziale |
| Całka nieoznaczona | Rodzina funkcji pierwotnych, przesuniętych wzdłuż osi y |
Czytaj więcej: Jak pomóc dziecku, któremu na niczym nie zależy? Skuteczne rady
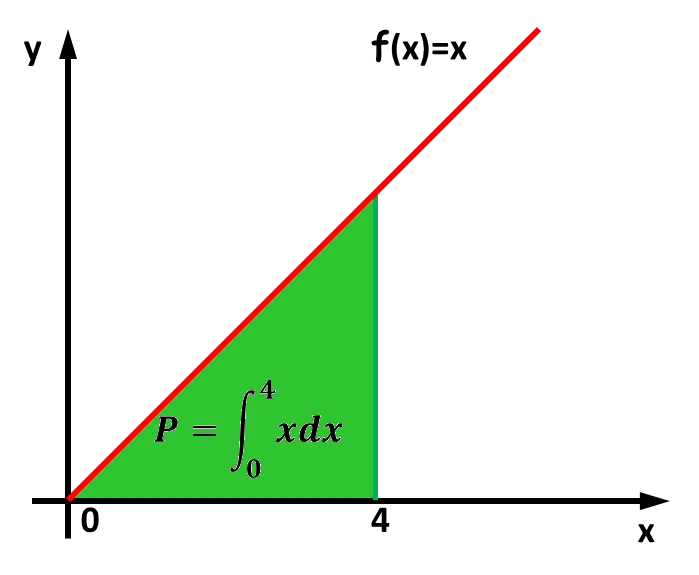
Przykłady zastosowania całek w różnych dziedzinach matematyki
Przykłady zastosowania całek są niezwykle istotne, ponieważ pokazują, jak te pojęcia są wykorzystywane w praktyce. Całki oznaczone i nieoznaczone znajdują zastosowanie w wielu dziedzinach, takich jak fizyka, inżynieria, a także w ekonomii. Zrozumienie, jak całki mogą być używane do rozwiązywania rzeczywistych problemów, jest kluczowe dla studentów i profesjonalistów w tych dziedzinach. W kolejnych akapitach przedstawimy konkretne przykłady, które ilustrują praktyczne zastosowania obu typów całek.
Przykłady całki oznaczonej w obliczeniach i zastosowaniach
Jednym z najczęstszych zastosowań całek oznaczonych jest obliczanie pól powierzchni. Na przykład, aby obliczyć pole pod krzywą funkcji f(x) = x^2 w przedziale od 0 do 3, możemy użyć całki oznaczonej. Wynik tego obliczenia to 9, co oznacza, że pole pod krzywą wynosi 9 jednostek kwadratowych. Takie obliczenia są niezbędne w inżynierii, gdzie precyzyjne określenie powierzchni jest kluczowe w projektowaniu i analizie.
Innym przykładem jest obliczanie objętości brył obrotowych. Na przykład, aby znaleźć objętość bryły powstałej przez obrót funkcji f(x) = x^2 wokół osi x, stosujemy całkę oznaczoną. Obliczenia te pozwalają na określenie objętości brył, co jest niezwykle istotne w inżynierii mechanicznej i budownictwie. Dzięki całkom oznaczonym, inżynierowie mogą dokładnie przewidzieć, jak materiały będą się zachowywać w różnych warunkach.
Przykłady całki nieoznaczonej w analizie matematycznej
Całki nieoznaczone mają również wiele zastosowań w matematyce, zwłaszcza w kontekście rozwiązywania równań różniczkowych. Na przykład, równanie różniczkowe dy/dx = 3x^2 można rozwiązać, stosując całkę nieoznaczoną. Po zintegrowaniu, otrzymujemy funkcję y = x^3 + C, gdzie C to stała integracji. To podejście jest kluczowe w wielu dziedzinach, takich jak fizyka, gdzie modele matematyczne opisują zjawiska naturalne.
Innym przykładem zastosowania całki nieoznaczonej jest znajdowanie funkcji pierwotnych. Na przykład, dla funkcji f(x) = 2x, całka nieoznaczona prowadzi nas do F(x) = x^2 + C. Funkcje pierwotne są niezwykle ważne w analizie matematycznej, ponieważ pozwalają na określenie zachowania funkcji w różnych przedziałach. Dzięki całkom nieoznaczonym, matematycy mogą modelować i przewidywać różne zjawiska, co jest kluczowe w badaniach naukowych.
Przykłady całki nieoznaczonej w analizie matematycznej
Całki nieoznaczone odgrywają kluczową rolę w analizie matematycznej, a ich zastosowanie w rzeczywistych problemach jest niezwykle istotne. Na przykład, w kontekście równań różniczkowych, całki nieoznaczone pozwalają na znalezienie funkcji pierwotnych, co jest kluczowe dla rozwiązywania problemów związanych z dynamiką ruchu. Równania takie jak dy/dx = 4x pokazują, jak całka nieoznaczona może prowadzić do funkcji y = 2x^2 + C, gdzie C jest stałą integracyjną. Dzięki temu inżynierowie i naukowcy mogą modelować różne zjawiska fizyczne, takie jak ruch ciał w przestrzeni.Innym przykładem zastosowania całki nieoznaczonej jest analiza funkcji w kontekście ekonomicznym. Na przykład, całka nieoznaczona funkcji popytu może pomóc w określeniu całkowitych przychodów w danym przedziale czasowym. Jeśli mamy funkcję popytu opisaną równaniem P(x) = 100 - 2x, całka nieoznaczona tej funkcji pozwala na obliczenie całkowitych przychodów, co jest niezbędne do podejmowania decyzji biznesowych. Dzięki tym zastosowaniom, całki nieoznaczone stają się nie tylko narzędziem teoretycznym, ale także praktycznym w różnych dziedzinach życia.
Praktyczne zastosowania całek w analizie danych i uczeniu maszynowym
W dobie rosnącej ilości danych, całki nieoznaczone i ich właściwości stają się kluczowe w kontekście analizy danych i uczenia maszynowego. W szczególności, techniki takie jak regresja liniowa mogą być zrozumiane i rozwijane przy użyciu całek, co pozwala na modelowanie złożonych zjawisk. Na przykład, w przypadku analizy trendów czasowych, całki mogą być używane do wygładzania danych, co ułatwia identyfikację wzorców i anomalii. W ten sposób, integracja funkcji może prowadzić do lepszego przewidywania przyszłych wartości, co jest niezwykle przydatne w biznesie i finansach.
Dodatkowo, w kontekście uczenia maszynowego, całki odgrywają rolę w optymalizacji funkcji kosztu. W procesie trenowania modeli, całki mogą być wykorzystywane do obliczania wartości funkcji, które pomagają w dostosowywaniu parametrów modelu. Dzięki zastosowaniu technik takich jak gradient descent, możliwe jest efektywne znajdowanie minimum funkcji kosztu, co prowadzi do lepszych wyników w predykcji i klasyfikacji. W miarę jak technologia rozwija się, zrozumienie i umiejętność stosowania całek w tych kontekstach będą coraz bardziej cenione w różnych branżach.