Zmienna zależna w matematyce to kluczowy koncept, który odnosi się do zmiennych, gdzie jedna zmienna zależy od drugiej. W kontekście funkcji matematycznych, zmienna zależna jest tą, której wartość zmienia się w odpowiedzi na zmiany innej zmiennej, zwanej zmienną niezależną. Zrozumienie tego pojęcia jest niezbędne do analizy i rozwiązywania problemów matematycznych.
W niniejszym artykule przyjrzymy się bliżej zmiennej zależnej, jej właściwościom oraz zastosowaniom w różnych funkcjach matematycznych. Omówimy również, jak wizualizacja tych zmiennych może pomóc w lepszym zrozumieniu ich relacji. Dzięki temu zdobędziesz wiedzę, która pozwoli Ci lepiej radzić sobie z zagadnieniami matematycznymi w codziennym życiu.
Kluczowe informacje:- Zmienna zależna to wartość, która zmienia się w odpowiedzi na zmiany zmiennej niezależnej.
- W matematyce, zmienne zależne i niezależne są podstawowymi elementami funkcji.
- Przykłady funkcji matematycznych z zmiennymi zależnymi obejmują funkcje liniowe i kwadratowe.
- Wizualizacja zmiennych zależnych i niezależnych za pomocą wykresów ułatwia zrozumienie ich relacji.
- Praktyczne zastosowania zmiennych zależnych występują w różnych dziedzinach, takich jak ekonomia czy nauki przyrodnicze.
Zmienna zależna w matematyce – definicja i podstawy pojęcia
Zmienna zależna w matematyce to kluczowy element, który odnosi się do sytuacji, w której jedna zmienna jest uzależniona od innej. W praktyce oznacza to, że wartość zmiennej zależnej zmienia się w odpowiedzi na zmiany zmiennej niezależnej. Na przykład, w funkcji matematycznej, zmienna zależna może reprezentować wynik obliczeń, który jest wynikiem działania zmiennej niezależnej. Zrozumienie tego pojęcia jest istotne dla analizy funkcji i równań matematycznych.W kontekście matematyki, zmienne zależne są używane w różnych rodzajach funkcji, takich jak funkcje liniowe, kwadratowe czy wykładnicze. Charakterystyka zmiennej zależnej polega na tym, że jej wartość jest bezpośrednio związana z wartością zmiennej niezależnej. To z kolei pozwala na modelowanie rzeczywistych zjawisk oraz analizę danych w różnych dziedzinach, takich jak ekonomia, fizyka czy biologia.
Czym jest zmienna zależna i jak działa w matematyce?
Zmienna zależna to pojęcie, które odnosi się do wartości, które są wynikiem działania zmiennych niezależnych. W matematyce, zmienna zależna często jest oznaczana jako "y", podczas gdy zmienna niezależna to zazwyczaj "x". W funkcji matematycznej, zmienna zależna przyjmuje różne wartości w zależności od wartości zmiennej niezależnej. Na przykład, w równaniu y = 2x + 3, wartość y (zmiennej zależnej) zmienia się w zależności od wartości x (zmiennej niezależnej).
Różnice między zmienną zależną a niezależną w funkcjach
Różnice między zmienną zależną a niezależną są kluczowe dla zrozumienia funkcji matematycznych. Zmienna niezależna to ta, która jest manipulowana lub zmieniana w eksperymencie, podczas gdy zmienna zależna reaguje na te zmiany. Na przykład, w badaniach naukowych, zmienna niezależna może być czasem, a zmienna zależna może być ilością produktu wytworzonego w danym czasie. Zrozumienie tej różnicy pozwala na skuteczniejsze modelowanie zjawisk oraz analizę wyników.
Zastosowanie zmiennych zależnych w funkcjach matematycznych
Zrozumienie, jak zmienne zależne są wykorzystywane w różnych funkcjach matematycznych, jest kluczowe dla efektywnej analizy danych i rozwiązywania problemów. W matematyce, zmienne zależne są często związane z wynikami, które są efektem działania zmiennych niezależnych. Przykładowo, w funkcjach liniowych i kwadratowych, zmienne zależne mogą reprezentować wyniki obliczeń, które zmieniają się w zależności od wartości zmiennych niezależnych. Dzięki temu możemy modelować różne zjawiska, co jest przydatne w wielu dziedzinach, takich jak ekonomia, inżynieria czy nauki przyrodnicze.
W praktyce, zmienne zależne odgrywają kluczową rolę w analizie funkcji matematycznych. Na przykład, w funkcji kwadratowej, zmienna zależna jest uzależniona od kwadratu zmiennej niezależnej, co prowadzi do charakterystycznego kształtu wykresu. To zjawisko można zaobserwować w różnych zastosowaniach, takich jak obliczenia związane z ruchem ciał w fizyce czy analiza trendów w ekonomii. Zrozumienie, jak zmienne zależne współdziałają z innymi zmiennymi, pozwala na lepsze prognozowanie i podejmowanie decyzji opartych na danych.
Przykłady funkcji matematycznych z zmiennymi zależnymi
W matematyce istnieje wiele funkcji, które ilustrują zastosowanie zmiennych zależnych. Przykładowe funkcje to:
- Funkcja liniowa: y = mx + b, gdzie y jest zmienną zależną, a m i b są stałymi.
- Funkcja kwadratowa: y = ax² + bx + c, w której zmienna y zależy od kwadratu zmiennej x.
- Funkcja wykładnicza: y = a * e^(bx), gdzie zmienna y zmienia się w zależności od zmiennej x w sposób wykładniczy.
Te funkcje pokazują, jak zmienne zależne są używane w różnych kontekstach, umożliwiając modelowanie rzeczywistych zjawisk i analizy matematyczne. Zrozumienie tych funkcji jest kluczowe dla dalszej nauki i zastosowań matematyki w praktyce.
Jak zmienne zależne wpływają na kształt wykresu funkcji?
Zależna w matematyce ma istotny wpływ na kształt wykresu funkcji. Kiedy zmienna zależna zmienia się w odpowiedzi na zmiany zmiennej niezależnej, kształt wykresu odzwierciedla te zmiany. Na przykład, w funkcji liniowej, zmienna zależna rośnie lub maleje w stałym tempie, co prowadzi do prostoliniowego wykresu. W przypadku funkcji kwadratowej, zmienna zależna zmienia się w sposób nieliniowy, co skutkuje parabolicznym kształtem wykresu. Te różnice w kształcie wykresu są kluczowe dla zrozumienia relacji między zmiennymi i analizy danych.
Czytaj więcej: Jak przygotować gry terenowe dla dzieci - kompletny poradnik organizacji
Wizualizacja zależności między zmiennymi w matematyce
Wizualizacja zmiennych jest niezbędnym narzędziem w matematyce, które pozwala na lepsze zrozumienie relacji między zmiennymi zależnymi a niezależnymi. Wykresy stanowią graficzną reprezentację funkcji, co umożliwia szybkie zauważenie trendów oraz wzorców. Dzięki wizualizacji można łatwiej analizować dane, identyfikować anomalie oraz przewidywać przyszłe wartości. Użycie różnych typów wykresów, takich jak wykresy liniowe, słupkowe czy kołowe, pozwala na przedstawienie informacji w sposób najbardziej odpowiedni do analizowanego problemu.
W kontekście edukacji, umiejętność wizualizacji danych jest kluczowa dla uczniów i studentów, którzy muszą zrozumieć złożone koncepcje matematyczne. Wykresy pomagają w nauce poprzez przedstawienie trudnych pojęć w bardziej przystępny sposób. Warto zwrócić uwagę na to, że dobre wizualizacje powinny być czytelne, zrozumiałe i dokładnie przedstawiać analizowane dane. Umożliwia to lepsze przyswajanie wiedzy i rozwijanie umiejętności analitycznych.
Jak tworzyć wykresy ilustrujące zmienne zależne i niezależne?
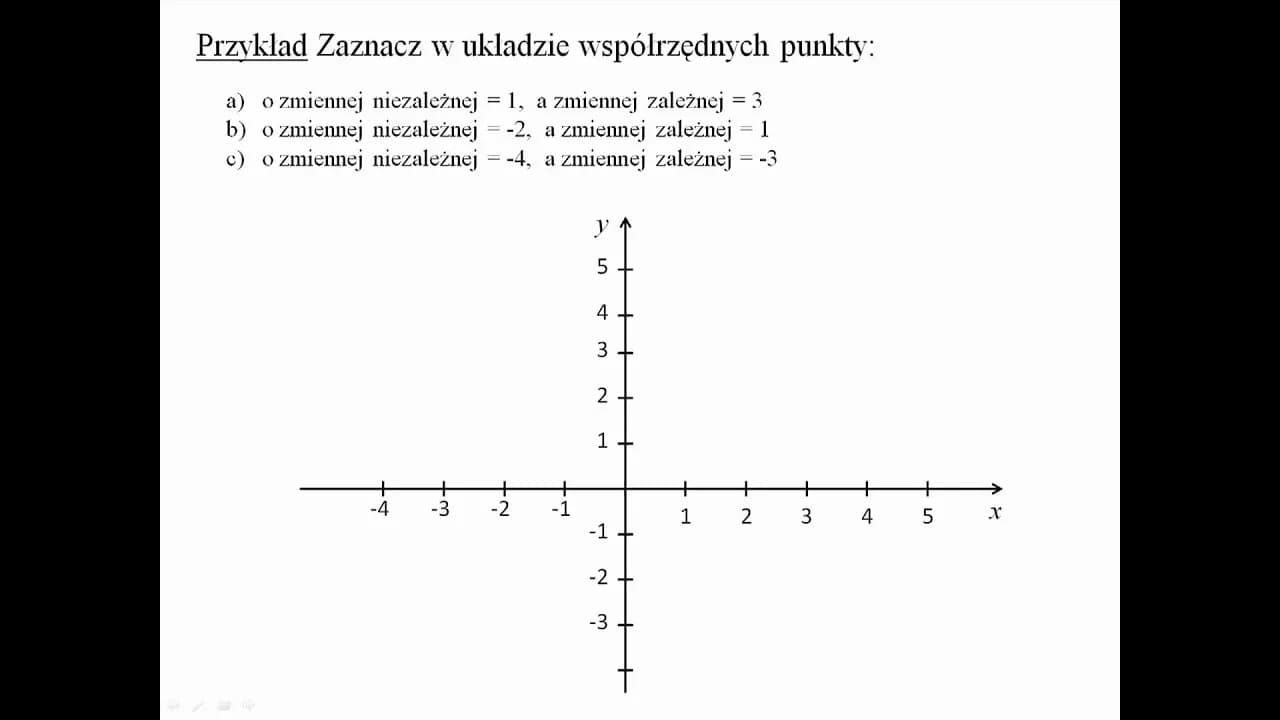
Aby stworzyć wykresy ilustrujące zmienne zależne i niezależne, należy wykonać kilka kluczowych kroków. Po pierwsze, zidentyfikuj zmienną niezależną, którą będziesz umieszczać na osi X, oraz zmienną zależną, która znajdzie się na osi Y. Następnie, zbierz dane, które będą użyte do wykresu, upewniając się, że są one dokładne i reprezentatywne. Kolejnym krokiem jest narysowanie układu współrzędnych, gdzie osie są odpowiednio oznaczone. Na końcu, wprowadź punkty danych na wykresie i połącz je, jeśli jest to konieczne, aby zobrazować relację między zmiennymi.
Rola wykresów w zrozumieniu funkcji matematycznych
Wykresy odgrywają kluczową rolę w zrozumieniu funkcji matematycznych, szczególnie w kontekście relacji między zmiennymi. Dzięki nim można łatwo zobaczyć, jak zmienna zależna reaguje na zmiany zmiennej niezależnej. Wykresy pomagają w identyfikacji trendów, wzorców i anomalii, co jest nieocenione w analizie danych. Umożliwiają także wizualizację bardziej złożonych koncepcji matematycznych, co czyni je bardziej przystępnymi dla uczniów i studentów. W rezultacie, umiejętność interpretacji wykresów jest niezbędna dla każdego, kto pragnie zrozumieć i stosować matematykę w praktyce.
Praktyczne zastosowania zmiennych zależnych w życiu codziennym
Zależna w matematyce ma wiele praktycznych zastosowań, które są widoczne w różnych dziedzinach życia codziennego. Zmienne zależne są kluczowe w analizie danych, umożliwiając przewidywanie wyników na podstawie dostępnych informacji. Na przykład, w ekonomii zmienne zależne mogą reprezentować dochody, które zmieniają się w zależności od wydatków konsumpcyjnych. W naukach przyrodniczych, zmienne te mogą ilustrować, jak zmiany temperatury wpływają na reakcje chemiczne. Zrozumienie tych zależności pozwala na podejmowanie lepszych decyzji i optymalizację procesów.
W kontekście zdrowia, zmienne zależne są istotne w analizie danych medycznych. Na przykład, poziom cholesterolu (zmienna zależna) może być analizowany w kontekście diety i stylu życia (zmienne niezależne). Takie analizy pomagają lekarzom w opracowywaniu skutecznych planów leczenia. W marketingu, zmienne zależne mogą dotyczyć sprzedaży, która zmienia się w odpowiedzi na kampanie promocyjne. W każdym z tych przypadków, zrozumienie zmiennych zależnych pozwala na lepsze prognozowanie i efektywniejsze działania.
Jak zmienne zależne pomagają w rozwiązywaniu problemów?
Zmienne zależne odgrywają kluczową rolę w rozwiązywaniu problemów w różnych dziedzinach. Dzięki nim można analizować, jak różne czynniki wpływają na wyniki i podejmować świadome decyzje. Na przykład, w edukacji, nauczyciele mogą wykorzystać zmienne zależne do oceny postępów uczniów, analizując, jak zmiany w metodach nauczania wpływają na wyniki testów. W biznesie, menedżerowie mogą badać, jak zmiany w strategiach marketingowych wpływają na sprzedaż, co pozwala na optymalizację działań. Takie podejście do analizy problemów prowadzi do bardziej efektywnych rozwiązań i lepszych wyników.
Przykłady zastosowań zmiennych zależnych w różnych dziedzinach
Zmienne zależne znajdują zastosowanie w wielu dziedzinach, takich jak:
- Ekonomia: Zmienne zależne mogą ilustrować, jak zmiany w polityce monetarnej wpływają na inflację.
- Fizyka: W analizie ruchu, prędkość (zmienna zależna) zmienia się w zależności od czasu (zmienna niezależna).
- Biologia: Badania nad wpływem diety na zdrowie, gdzie poziom glukozy we krwi jest zmienną zależną.
Te przykłady pokazują, jak zmienne zależne są wykorzystywane do analizy i zrozumienia złożonych zjawisk w różnych dziedzinach, co pozwala na podejmowanie lepszych decyzji i rozwiązywanie problemów.
| Dyscyplina | Przykład zastosowania zmiennych zależnych |
| Ekonomia | Analiza wpływu stóp procentowych na inflację |
| Fizyka | Badanie ruchu obiektów w zależności od czasu |
| Biologia | Wpływ diety na poziom cholesterolu |
Jak zmienne zależne wpłyną na przyszłość analizy danych?
W miarę jak technologia i analiza danych stają się coraz bardziej zaawansowane, zmienne zależne będą odgrywać kluczową rolę w rozwoju inteligentnych systemów analitycznych. Przykładowo, w dziedzinie sztucznej inteligencji i uczenia maszynowego, zrozumienie, jak zmienne zależne wpływają na wyniki, pozwala na tworzenie modeli, które są w stanie przewidywać przyszłe zachowania użytkowników czy trendy rynkowe. Dzięki zaawansowanym algorytmom, które analizują ogromne zbiory danych, zmienne zależne mogą być wykorzystywane do identyfikacji wzorców, co może prowadzić do bardziej precyzyjnych prognoz i lepszej personalizacji usług.W przyszłości, integracja zmiennych zależnych z technologią Internetu Rzeczy (IoT) stworzy nowe możliwości w zakresie monitorowania i optymalizacji procesów w czasie rzeczywistym. Na przykład, w inteligentnych domach, zmienne zależne mogą być używane do analizy zużycia energii w zależności od nawyków mieszkańców, co pozwala na automatyczne dostosowywanie ustawień w celu zwiększenia efektywności energetycznej. Takie innowacje nie tylko poprawią komfort życia, ale także przyczynią się do zrównoważonego rozwoju i oszczędności zasobów.
