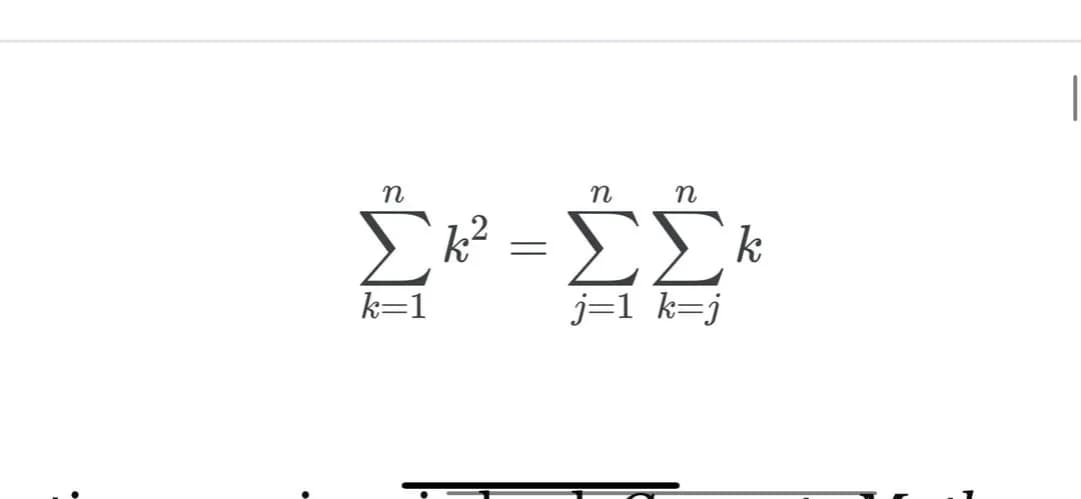
W matematyce znaki i symbole odgrywają kluczową rolę, umożliwiając precyzyjne wyrażanie pojęć i relacji. Zrozumienie ich znaczenia jest niezbędne dla każdego, kto chce zgłębiać tajniki tego przedmiotu. W tym artykule przyjrzymy się podstawowym symbolom matematycznym, ich zastosowaniom oraz kontekstom, w jakich są używane.
Od znaków równości i dodawania po bardziej zaawansowane symbole, takie jak litera grecka epsilon czy notacja naukowa, każdy z tych elementów ma swoje unikalne znaczenie. Poprzez naukę o symbolach matematycznych zyskamy lepsze zrozumienie zarówno prostych, jak i bardziej złożonych zagadnień matematycznych.
Najistotniejsze informacje:- Symbole matematyczne mają różne znaczenia w zależności od kontekstu.
- Znak równości jest kluczowy do zrozumienia równań, a znaki dodawania i odejmowania są podstawowymi operacjami arytmetycznymi.
- W algebrze ważne są symbole mnożenia, dzielenia oraz potęgowania, które mają swoje specyficzne zastosowania.
- Niektóre symbole, takie jak epsilon, mają szczególne znaczenie w analizie matematycznej.
- Notacja naukowa, np. $$e+$$, jest używana do zapisu dużych liczb w zwięzły sposób.
- Warto być świadomym powszechnych błędów w interpretacji symboli matematycznych, aby uniknąć nieporozumień.
Zrozumienie podstawowych symboli matematycznych i ich znaczenia
W matematyce znaki i symbole są kluczowe dla zrozumienia różnych pojęć i operacji. Dzięki nim możemy precyzyjnie wyrażać relacje między liczbami i zmiennymi. Każdy symbol ma swoje konkretne znaczenie, które może się różnić w zależności od kontekstu. Zrozumienie podstawowych symboli, takich jak znak równości czy symbole dodawania i odejmowania, jest pierwszym krokiem w nauce matematyki.
Te podstawowe symbole matematyczne stanowią fundament dla bardziej zaawansowanych koncepcji. Bez ich znajomości trudno jest zrozumieć bardziej skomplikowane operacje i pojęcia, które pojawiają się w algebrze czy analizie matematycznej. Dlatego warto poświęcić czas na naukę ich znaczenia i zastosowania, co ułatwi dalsze zgłębianie matematyki.Znak równości: Klucz do zrozumienia równań
Znak równości (=) jest jednym z najważniejszych symboli w matematyce, ponieważ oznacza, że obie strony równania są sobie równe. Używamy go, aby wskazać, że dwie wartości są identyczne. Na przykład w równaniu $$2 + 2 = 4$$ widzimy, że suma dwóch i dwóch wynosi cztery. Znak równości pozwala nam na formułowanie równań, które są podstawą wielu zagadnień matematycznych.
- Równania z użyciem znaku równości są podstawą w algebrze i arytmetyce.
- Użycie znaku równości jest kluczowe w dowodach matematycznych, gdzie musimy wykazać, że dwie wartości są równe.
- Równania mogą być proste, jak $$x + 3 = 5$$, lub bardziej złożone, z wieloma zmiennymi.
Znak dodawania i odejmowania: Podstawowe operacje arytmetyczne
W matematyce znaki dodawania (+) i odejmowania (-) są podstawowymi symbolami, które pozwalają na wykonywanie prostych operacji arytmetycznych. Dodawanie to proces łączenia dwóch lub więcej liczb, co prowadzi do uzyskania ich sumy. Na przykład, w równaniu $$3 + 2$$, dodajemy trzy i dwa, co daje wynik pięć. Z kolei odejmowanie polega na usunięciu jednej wartości od drugiej, co ilustruje równanie $$5 - 1$$, które daje wynik cztery.
Te podstawowe operacje są fundamentem matematyki i stanowią punkt wyjścia do bardziej złożonych zagadnień. Bez umiejętności dodawania i odejmowania trudno byłoby zrozumieć bardziej skomplikowane operacje, takie jak mnożenie czy dzielenie. Dlatego warto ćwiczyć te umiejętności, aby stać się pewnym siebie w matematyce.
Znaki i symbole w algebrze: Ich rola i zastosowanie
W algebrze symbole mają szczególne znaczenie, ponieważ pozwalają na wyrażanie bardziej skomplikowanych relacji i operacji. Symbole mnożenia (×) i dzielenia (÷) są niezbędne do wykonywania tych operacji, które są kluczowe w rozwiązywaniu równań. Na przykład, w równaniu $$4 \times 5$$, mnożymy cztery przez pięć, co daje dwadzieścia. Z kolei $$20 ÷ 4$$ oznacza, że dwadzieścia dzielimy przez cztery, co daje pięć. Te operacje są podstawą wielu działań w algebrze.
W algebrze często używa się także symbolu potęgowania (^), który pozwala na wyrażenie liczby w formie wykładniczej. Na przykład, $$2^3$$ oznacza, że dwa podnosimy do trzeciej potęgi, co daje osiem. Wszystkie te symbole są niezwykle ważne, ponieważ umożliwiają rozwiązywanie bardziej skomplikowanych problemów matematycznych i tworzenie równań, które są kluczowe w różnych dziedzinach nauki.
Symbol mnożenia i dzielenia: Zrozumienie operacji
W matematyce symbole mnożenia (×) i dzielenia (÷) są kluczowe dla wykonywania podstawowych operacji arytmetycznych. Symbol mnożenia oznacza, że dwie liczby są łączone w celu uzyskania ich iloczynu. Na przykład w równaniu $$3 \times 4$$, mnożymy trzy przez cztery, co daje wynik dwanaście. Z kolei symbol dzielenia wskazuje, że jedna liczba jest dzielona przez drugą, jak w równaniu $$12 ÷ 3$$, które daje wynik cztery.
Te operacje są niezbędne w algebrze, ponieważ pozwalają na rozwiązywanie równań i wyrażanie bardziej złożonych relacji. Mnożenie i dzielenie są również używane w różnych kontekstach, takich jak obliczenia dotyczące powierzchni, objętości czy proporcji. Zrozumienie tych symboli jest kluczowe dla dalszego zgłębiania matematyki i jej zastosowań w codziennym życiu.
Znak potęgowania: Jak interpretować wykładniki
Symbol potęgowania (^) jest używany do wyrażania liczby w formie wykładniczej, co oznacza, że liczba jest podnoszona do określonej potęgi. Na przykład w równaniu $$2^3$$, liczba dwa jest podnoszona do trzeciej potęgi, co daje wynik osiem. Potęgowanie jest ważnym narzędziem w matematyce, ponieważ pozwala na skrócenie zapisu dużych liczb oraz uproszczenie obliczeń.
Potęgowanie znajduje zastosowanie w różnych dziedzinach, takich jak geometria, gdzie obliczamy pole powierzchni czy objętość figur przestrzennych. Dzięki potęgom możemy również wyrażać wzrosty lub spadki w kontekście finansowym, na przykład w obliczeniach dotyczących oprocentowania. Zrozumienie symbolu potęgowania i jego zastosowań jest niezbędne dla każdego, kto chce zgłębiać bardziej zaawansowane zagadnienia matematyczne.Czytaj więcej: Co to jest debet w matematyce i dlaczego może Cię zmylić?
Specjalne symbole matematyczne: Ich znaczenie w różnych kontekstach
W matematyce istnieje wiele specjalnych symboli, które mają różne znaczenia w zależności od kontekstu, w jakim są używane. Na przykład, mała litera grecka epsilon ($$\epsilon$$) jest często stosowana w analizie matematycznej, gdzie oznacza dowolnie małą liczbę dodatnią. Jest to szczególnie istotne w kontekście granic i pochodnych, gdzie epsilon pozwala na precyzyjne określenie, jak blisko możemy zbliżyć się do wartości granicznej. Ponadto, epsilon może reprezentować błąd w statystyce, co czyni go wszechobecnym symbolem w różnych dziedzinach matematyki.
Innym ważnym symbolem jest pionowa kreska ($$|$$), która oznacza "dzieli" w kontekście podzielności. Na przykład, w wyrażeniu $$a|b$$, symbol ten wskazuje, że liczba $$a$$ dzieli liczbę $$b$$ bez reszty. Oprócz tego, inne symbole, takie jak notacja naukowa ($$e+$$ lub $$e-$$), są używane do zapisu dużych liczb w bardziej przystępny sposób. Zrozumienie tych symboli jest kluczowe dla każdego, kto pragnie zgłębiać tajniki matematyki i jej zastosowań w praktyce.
Mała litera grecka epsilon: Co oznacza w analizie
Mała litera grecka epsilon ($$\epsilon$$) odgrywa istotną rolę w analizie matematycznej, szczególnie w kontekście granic. Symbol ten jest używany do określenia, jak blisko wartości granicznej możemy się zbliżyć, co jest kluczowe w definicji granicy funkcji. Na przykład, w definicji granicy, mówimy, że dla każdej dodatniej liczby $$\epsilon$$ istnieje liczba $$\delta$$, taka że jeśli różnica między argumentem a punktem granicznym jest mniejsza niż $$\delta$$, to różnica wartości funkcji jest mniejsza niż $$\epsilon$$. Dzięki temu epsilon pozwala na precyzyjne określenie, jak funkcja zachowuje się w pobliżu punktu granicznego.
- Symbol epsilon jest kluczowy w dowodach dotyczących granic i ciągłości funkcji.
- W statystyce epsilon może reprezentować margines błędu w analizach danych.
- Użycie epsilon w analizie rzeczywistej pozwala na dokładniejsze zrozumienie zachowania funkcji w pobliżu punktów granicznych.
Symbol pionowej kreski: Zastosowanie w teorii liczb
Symbol pionowej kreski ($$|$$) jest istotnym elementem w teorii liczb, gdzie oznacza, że jedna liczba dzieli drugą bez reszty. Na przykład, w zapisie $$a|b$$, symbol ten wskazuje, że liczba $$a$$ jest dzielnikiem liczby $$b$$. To oznacza, że $$b$$ można podzielić przez $$a$$, uzyskując liczbę całkowitą jako wynik. Użycie pionowej kreski jest kluczowe w analizie podzielności, co jest podstawowym zagadnieniem w teorii liczb.
W praktyce, symbol pionowej kreski jest często wykorzystywany do określenia, czy liczby są względnie pierwsze. Na przykład, jeśli $$a = 3$$ i $$b = 9$$, to możemy zapisać $$3|9$$, co oznacza, że trzy dzieli dziewięć. Pionowa kreska jest również używana w kontekście zbiorów, gdzie może oznaczać, że element należy do określonego zbioru. Zrozumienie tego symbolu jest kluczowe dla dalszego zgłębiania teorii liczb i operacji związanych z podzielnością.

Notacja naukowa: Jak czytać i używać symboli
Notacja naukowa to sposób zapisu dużych lub małych liczb w formie, która jest bardziej zrozumiała i łatwiejsza do przetwarzania. W notacji naukowej liczba jest przedstawiana jako iloczyn liczby między 1 a 10 oraz potęgi dziesięciu. Na przykład, liczba $$6.89 \times 10^{12}$$ oznacza 6.89 pomnożone przez 1 bilion. Taki zapis jest szczególnie przydatny w naukach ścisłych, gdzie często mamy do czynienia z bardzo dużymi lub bardzo małymi wartościami.
Notacja naukowa ułatwia również wykonywanie obliczeń, ponieważ pozwala na łatwe dodawanie, odejmowanie, mnożenie i dzielenie liczb w tej formie. Na przykład, aby dodać dwie liczby w notacji naukowej, należy upewnić się, że mają one tę samą potęgę dziesięciu. Jeśli mamy $$2 \times 10^3$$ i $$3 \times 10^3$$, możemy je dodać, uzyskując $$5 \times 10^3$$. Zrozumienie notacji naukowej jest kluczowe dla każdego, kto pracuje z dużymi danymi lub w dziedzinach wymagających precyzyjnych obliczeń.
Praktyczne zastosowania notacji naukowej w codziennym życiu
Notacja naukowa ma zastosowanie nie tylko w matematyce i naukach ścisłych, ale także w codziennym życiu. Ułatwia zrozumienie i obliczenia związane z dużymi wartościami, które często pojawiają się w finansach, inżynierii czy technologii. Na przykład, w analizach finansowych możemy spotkać się z dużymi kwotami, takimi jak budżety państwowe czy wartości rynkowe przedsiębiorstw, które można efektywnie zapisać w formie notacji naukowej. Dzięki temu, inwestorzy i analitycy mogą szybko porównywać różne wartości i podejmować lepsze decyzje.
W przyszłości, z uwagi na rosnącą ilość danych generowanych przez technologie, znajomość notacji naukowej stanie się jeszcze bardziej istotna. W obszarze big data, gdzie dane mogą mieć różne skale, umiejętność pracy z notacją naukową pozwoli na efektywne przetwarzanie i analizę informacji. Umożliwi to nie tylko szybsze obliczenia, ale także lepsze zrozumienie złożonych zjawisk, takich jak zmiany klimatyczne czy trendy rynkowe, co jest kluczowe dla podejmowania świadomych decyzji w różnych dziedzinach życia.