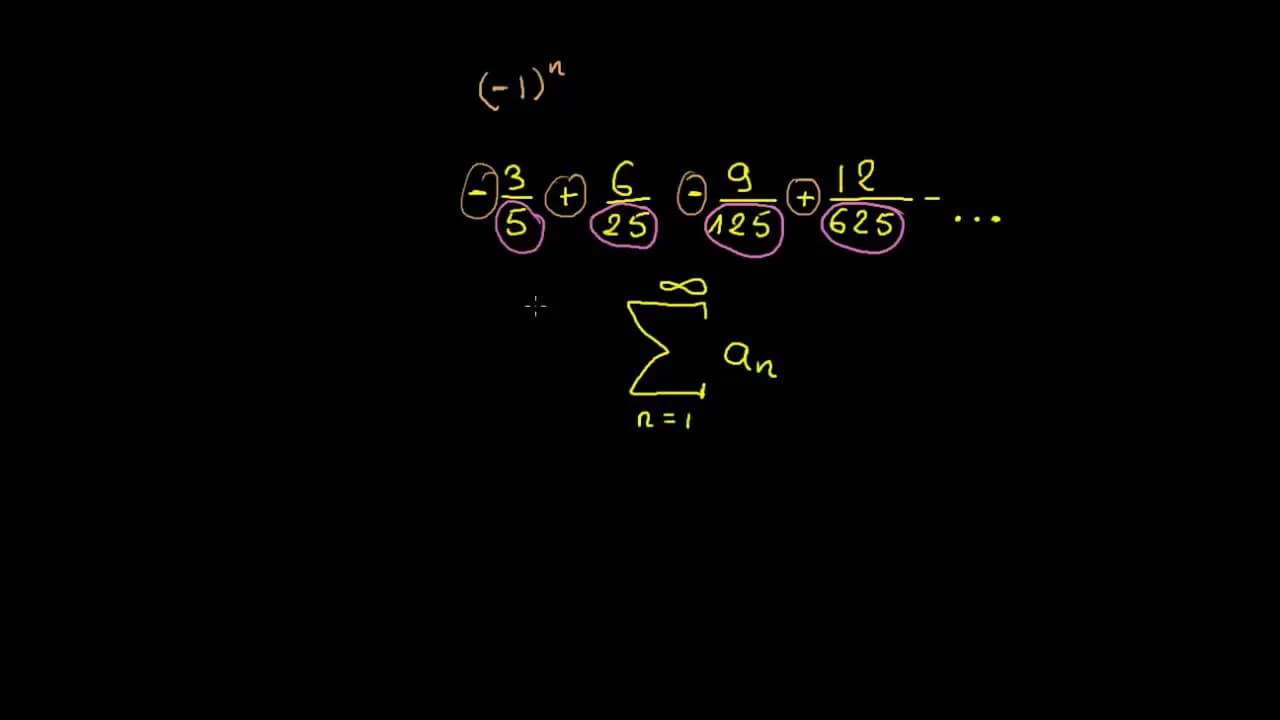Symbol sigma, oznaczany jako grecka litera Σ, jest kluczowym narzędziem w matematyce, które służy do skróconego zapisu sumy wielu wyrazów. Umożliwia on zwięzłe przedstawienie długich ciągów dodawania, co znacząco ułatwia obliczenia i analizę danych. Dzięki notacji sigma możemy łatwo zdefiniować granice sumowania, co jest szczególnie przydatne w różnych dziedzinach, takich jak statystyka czy ekonomia.
W artykule przyjrzymy się bliżej temu symbolowi, jego definicji oraz zastosowaniom w praktyce. Dowiemy się, jak stosować notację sigma do sumowania liczb oraz jakie ma ona znaczenie w analizie matematycznej. Pochodzenie symbolu sięga starożytnej Grecji, gdzie użycie liter greckich w matematyce stało się powszechne. Zrozumienie symbolu sigma jest kluczowe dla każdego, kto chce zgłębić tajniki matematyki i nauk ścisłych.
Najistotniejsze informacje:- Symbol sigma (Σ) jest używany do zapisu sumy wielu wyrazów w matematyce.
- Notacja sigma umożliwia zdefiniowanie granic sumowania, co upraszcza obliczenia.
- Przykład: $$\sum_{i=1}^{9} i$$ oznacza sumę liczb od 1 do 9.
- Symbol sigma ma zastosowanie w statystyce, analizie matematycznej i ekonomii.
- Pochodzenie symbolu sięga starożytnej Grecji, gdzie stał się on powszechnie używany.
Definicja symbolu sigma i jego znaczenie w matematyce
W matematyce symbol sigma, oznaczany jako grecka litera Σ, jest używany jako skrócony zapis sumy wielu wyrazów. Dzięki temu narzędziu, skomplikowane obliczenia stają się znacznie prostsze i bardziej zrozumiałe. Notacja sigma pozwala na zwięzłe przedstawienie długich ciągów dodawania, co jest szczególnie przydatne w różnych dziedzinach matematyki.
Wartość wyrażenia, takiego jak $$\sum_{i=1}^{n} i$$, oznacza sumę wszystkich liczb od 1 do n. Symbol ten ma kluczowe znaczenie w matematyce, ponieważ umożliwia definiowanie granic sumowania, gdzie zmienna (np. i) zmienia się od wartości początkowej do końcowej. Dzięki temu, obliczenia stają się bardziej przejrzyste i łatwiejsze do wykonania.
Jak wygląda notacja sigma i co oznacza?
Notacja sigma jest reprezentowana przez dużą literę grecką Σ i jest używana do oznaczania sumy. W praktyce, symbol ten jest często stosowany w połączeniu z dolnym i górnym indeksem, które definiują zakres sumowania. Na przykład, w zapisie $$\sum_{i=1}^{9} i$$, dolny indeks (1) wskazuje na początkową wartość, a górny indeks (9) na wartość końcową, co oznacza, że sumujemy wszystkie liczby od 1 do 9.
Wizualnie, notacja sigma przypomina literę E (epsilon) z dodatkowym „ogonem”, co czyni ją łatwą do rozpoznania. Dzięki tej prostocie, symbol sigma w matematyce stał się powszechnie akceptowany i używany w różnych kontekstach, zarówno w teorii, jak i w praktyce.
Dlaczego symbol sigma jest kluczowy w matematyce?
Symbol sigma ma fundamentalne znaczenie w matematyce, ponieważ pozwala na uproszczenie skomplikowanych obliczeń. Umożliwia on zwięzłe przedstawienie sum, co jest nieocenione w różnych dziedzinach matematyki, takich jak algebra, analiza matematyczna czy statystyka. Dzięki użyciu notacji sigma, matematycy mogą łatwo definiować sumy, co znacznie przyspiesza proces obliczeniowy i zwiększa przejrzystość formuł.
W wielu przypadkach, symbol sigma w matematyce jest kluczowym narzędziem do zrozumienia bardziej skomplikowanych koncepcji. Gdy operacje matematyczne stają się złożone, użycie tego symbolu pozwala na uproszczenie zapisu, co ułatwia zarówno naukę, jak i zastosowanie matematyki w praktyce. Dlatego też, jego obecność w różnych gałęziach matematyki jest nie tylko pożądana, ale wręcz niezbędna.
Przykłady zastosowania notacji sigma w obliczeniach
Notacja sigma jest szeroko stosowana w matematyce do wykonywania obliczeń sumacyjnych. Na przykład, gdy chcemy obliczyć sumę pierwszych dziesięciu liczb naturalnych, możemy użyć zapisu $$\sum_{i=1}^{10} i$$, co oznacza dodanie wszystkich liczb od 1 do 10. Dzięki temu, złożone obliczenia stają się prostsze i bardziej zrozumiałe, a wyniki można szybko uzyskać bez konieczności ręcznego dodawania każdej liczby.
W bardziej zaawansowanych zastosowaniach, zastosowanie notacji sigma w matematyce obejmuje obliczenia w statystyce, gdzie często sumuje się wartości w celu obliczenia średnich lub wariancji. Przykładem może być zapis $$\sum_{i=1}^{n} x_i$$, gdzie x_i to wartości w zbiorze danych. Takie podejście pozwala na efektywne analizowanie dużych zbiorów danych oraz uzyskiwanie istotnych informacji w krótszym czasie.
Jak używać notacji sigma do sumowania liczb?
Aby używać notacji sigma do sumowania liczb, należy najpierw zdefiniować zakres sumowania. Wskazujemy dolny i górny indeks, które określają, od jakiej wartości do jakiej wartości będziemy sumować. Na przykład, zapis $$\sum_{i=1}^{n} i$$ oznacza, że sumujemy wszystkie liczby od 1 do n, gdzie i jest zmienną, która przyjmuje wartości w tym zakresie.
Proces sumowania za pomocą notacji sigma jest prosty. Wybieramy wartość początkową (dolny indeks), wartość końcową (górny indeks) oraz funkcję, którą chcemy sumować. Na przykład, jeśli chcemy obliczyć sumę pierwszych pięciu liczb naturalnych, zapiszemy to jako $$\sum_{i=1}^{5} i$$, co daje wynik 1 + 2 + 3 + 4 + 5 = 15.
- Ciąg arytmetyczny: $$\sum_{i=1}^{n} a_i$$, gdzie a_i = a + (i-1)d, a to pierwszy wyraz, d to różnica.
- Ciąg geometryczny: $$\sum_{i=0}^{n} ar^i$$, gdzie a to pierwszy wyraz, a r to iloraz.
- Ciąg kwadratowy: $$\sum_{i=1}^{n} i^2$$, co oznacza sumę kwadratów pierwszych n liczb naturalnych.
Zastosowanie sigma w statystyce i analizie danych
Notacja sigma jest niezwykle przydatna w statystyce i analizie danych, ponieważ pozwala na efektywne obliczanie sum i średnich w dużych zbiorach danych. Dzięki symbolowi sigma, statystycy mogą szybko zdefiniować sumy wartości, co jest kluczowe przy obliczaniu takich miar jak średnia arytmetyczna, wariancja czy odchylenie standardowe. Na przykład, zapis $$\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i$$ oznacza obliczenie średniej wartości z n pomiarów, gdzie x_i to poszczególne obserwacje.
W praktyce, zastosowanie notacji sigma w matematyce w analizie danych pozwala na uproszczenie wielu obliczeń. Umożliwia to szybkie przetwarzanie danych oraz uzyskiwanie istotnych informacji z dużych zestawów danych. W poniższej tabeli przedstawiono kilka przykładów statystycznych formuł, które wykorzystują notację sigma, wraz z odpowiadającymi im danymi.
| Formuła | Opis |
|---|---|
| $$\sum_{i=1}^{n} x_i$$ | Całkowita suma wartości w zbiorze danych. |
| $$\bar{x} = \frac{1}{n} \sum_{i=1}^{n} x_i$$ | Średnia arytmetyczna z n wartości. |
| $$s^2 = \frac{1}{n-1} \sum_{i=1}^{n} (x_i - \bar{x})^2$$ | Wariancja zbioru danych. |
Czytaj więcej: Pary liczb, których suma jest równa iloczynowi – zaskakujące fakty matematyczne
Historyczne konteksty i rozwój symbolu sigma
Symbol sigma, oznaczany jako grecka litera Σ, ma swoje korzenie w starożytnej Grecji, gdzie użycie liter greckich w matematyce stało się powszechne. Jego wprowadzenie do notacji matematycznej miało miejsce w XIX wieku, kiedy to matematycy zaczęli poszukiwać efektywnych sposobów na zapisywanie sum. Wcześniej, sumy były często zapisywane w sposób opisowy, co było niepraktyczne i czasochłonne. Dzięki wprowadzeniu symbolu sigma, możliwe stało się zwięzłe przedstawienie długich ciągów dodawania, co znacznie ułatwiło pracę z równaniami matematycznymi.
W miarę jak rozwijała się matematyka, symbol sigma zyskał na znaczeniu i stał się integralną częścią nowoczesnej notacji matematycznej. Jego zastosowanie rozprzestrzeniło się na różne dziedziny, takie jak statystyka, analiza matematyczna czy ekonomia. Współczesne podejście do matematyki opiera się na jasnych i zrozumiałych zapisach, a symbol sigma w matematyce odgrywa kluczową rolę w tym procesie, umożliwiając matematykom i naukowcom efektywne przedstawienie skomplikowanych obliczeń.
Jak symbol sigma wpłynął na rozwój matematyki?
Symbol sigma miał znaczący wpływ na rozwój matematyki, wprowadzając nową jakość do zapisu obliczeń. Umożliwił on matematykom zwięzłe przedstawienie sum, co przyczyniło się do powstania bardziej skomplikowanych teorii matematycznych. Dzięki notacji sigma, wiele koncepcji matematycznych stało się bardziej przystępnych, co ułatwiło ich naukę i zastosowanie w praktyce. W rezultacie, symbol ten stał się nie tylko narzędziem, ale i fundamentem dla rozwoju matematyki jako nauki.
Kto wprowadził notację sigma do matematyki?
Notację sigma wprowadził do matematyki niemiecki matematyk Leonhard Euler w XVIII wieku. Jego prace miały ogromny wpływ na rozwój analizy matematycznej i teorii liczb. Euler był pionierem w wielu dziedzinach matematyki, a jego wprowadzenie symbolu sigma pozwoliło na uproszczenie zapisu sum. Dzięki jego innowacjom, symbol ten stał się standardem w matematyce, a jego znaczenie tylko rosło w miarę rozwoju nauk ścisłych.
Praktyczne zastosowania notacji sigma w analizie danych
Notacja sigma ma wiele praktycznych zastosowań, które mogą znacznie ułatwić analizę danych w różnych dziedzinach, takich jak ekonomia, nauki przyrodnicze czy informatyka. Na przykład, w analizie danych dotyczących sprzedaży, można wykorzystać notację sigma do obliczenia całkowitych przychodów z różnych produktów w określonym okresie. Dzięki temu, przedsiębiorstwa mogą szybko ocenić, które produkty przynoszą największe zyski, co umożliwia podejmowanie lepszych decyzji strategicznych.
W przyszłości, rozwój technologii takich jak uczenie maszynowe i sztuczna inteligencja może jeszcze bardziej zwiększyć znaczenie notacji sigma w analizie danych. Algorytmy, które wykorzystują sumy do obliczeń, mogą być zoptymalizowane dzięki zastosowaniu notacji sigma, co przyspieszy proces przetwarzania informacji. W rezultacie, umiejętność korzystania z tej notacji stanie się kluczowa dla analityków danych, którzy będą musieli szybko i efektywnie przetwarzać duże zbiory danych, aby uzyskać wartościowe wnioski.
