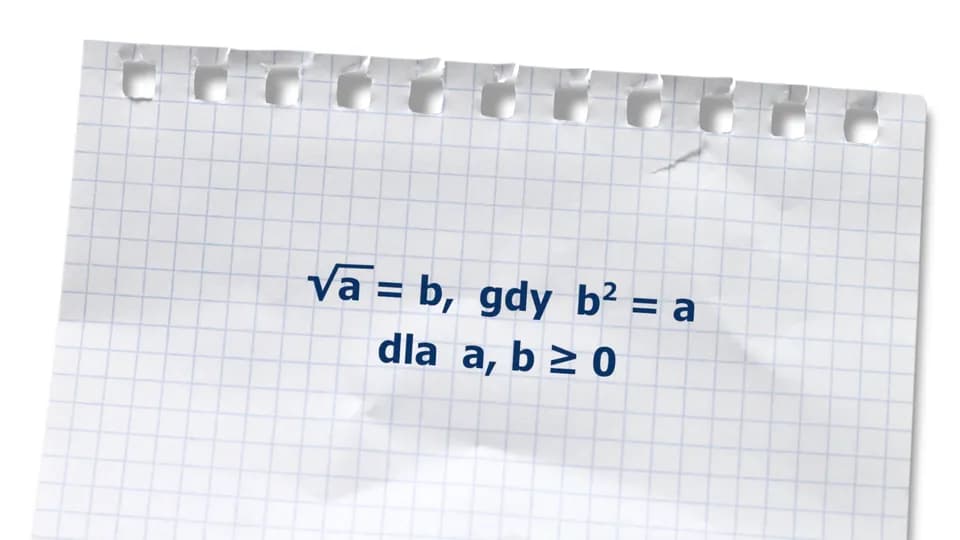Pierwiastek to istotny koncept w matematyce, który odgrywa kluczową rolę w wielu dziedzinach nauki. Definiuje się go jako liczbę, która podniesiona do określonej potęgi daje liczbę wyjściową. Na przykład, pierwiastek kwadratowy z liczby 9 to 3, ponieważ 3 podniesione do potęgi 2 równa się 9. Zrozumienie tego pojęcia jest fundamentem dla dalszej nauki matematyki, a także dla zastosowań w fizyce, inżynierii czy ekonomii.
W artykule omówimy różne rodzaje pierwiastków, ich zastosowania w praktyce oraz jak są wykorzystywane w różnych dziedzinach matematyki. Przyjrzymy się także wizualizacjom, które pomogą lepiej zrozumieć ten kluczowy koncept.
Kluczowe informacje:- Pierwiastek to liczba, która po podniesieniu do określonej potęgi daje liczbę wyjściową.
- Najpopularniejsze rodzaje pierwiastków to pierwiastek kwadratowy i pierwiastek sześcienny.
- Pierwiastki mają szerokie zastosowanie w matematyce, w tym w rozwiązywaniu równań i obliczeniach geometrycznych.
- Wizualizacje pierwiastków mogą pomóc w lepszym zrozumieniu ich właściwości i zastosowań.
- Znajomość pierwiastków jest niezbędna w wielu dziedzinach, takich jak fizyka i inżynieria.
Definicja pierwiastka w matematyce i jego znaczenie
Pierwiastek to fundamentalne pojęcie w matematyce, które odnosi się do liczby, która podniesiona do określonej potęgi daje liczbę wyjściową. Na przykład, pierwiastek kwadratowy z liczby 16 to 4, ponieważ 4 podniesione do potęgi 2 równa się 16. Definicja ta jest kluczowa dla zrozumienia wielu zagadnień matematycznych, w tym równań, funkcji oraz różnych zastosowań w naukach ścisłych.
Pierwiastki są nie tylko ważne w teorii matematycznej, ale także mają praktyczne zastosowanie w codziennym życiu. Bez znajomości pierwiastków trudno byłoby zrozumieć bardziej skomplikowane koncepcje, takie jak równania kwadratowe czy obliczenia geometryczne. W matematyce, pierwiastki pełnią rolę narzędzia do rozwiązywania problemów i analizy danych, co czyni je niezbędnym elementem w edukacji matematycznej.Co to jest pierwiastek i jak go zdefiniować?
Pierwiastek to liczba, która, gdy zostanie podniesiona do określonej potęgi, daje inną liczbę. Na przykład, pierwiastek kwadratowy z liczby 25 to 5, ponieważ 5 podniesione do potęgi 2 równa się 25. W matematycznej notacji, pierwiastek z liczby a zapisuje się jako √a. Istnieją różne typy pierwiastków, w tym pierwiastki kwadratowe i sześcienne, które mają swoje specyficzne zastosowania i znaczenie w różnych kontekstach.
Dlaczego pierwiastek jest ważny w matematyce?
Pierwiastek odgrywa kluczową rolę w matematyce, ponieważ jest podstawowym narzędziem do rozwiązywania równań i analizowania funkcji. Bez zrozumienia, czym jest pierwiastek, trudno jest pojąć bardziej skomplikowane koncepcje, takie jak równania kwadratowe czy funkcje trygonometryczne. Ponadto, pierwiastki są niezbędne w wielu dziedzinach nauki, w tym w fizyce i inżynierii, gdzie pomagają w obliczeniach związanych z prędkością, przyspieszeniem i innymi parametrami fizycznymi.
W praktyce, znajomość pierwiastków pozwala na lepsze zrozumienie zjawisk zachodzących w otaczającym nas świecie. Na przykład, pierwiastki są używane w obliczeniach dotyczących powierzchni i objętości różnych figur geometrycznych. Dzięki temu, pierwiastki są nie tylko teoretycznym pojęciem, ale mają także szerokie zastosowanie w rzeczywistych problemach matematycznych.
Rodzaje pierwiastków i ich zastosowanie w praktyce
Pierwiastki dzielą się na różne typy, z których najpopularniejsze to pierwiastek kwadratowy i pierwiastek sześcienny. Pierwiastek kwadratowy z liczby x to taka liczba, która, podniesiona do potęgi 2, daje x. Na przykład, pierwiastek kwadratowy z 9 to 3, ponieważ 3² = 9. Ten typ pierwiastka znajduje zastosowanie w wielu dziedzinach, takich jak geometria, gdzie oblicza się pole kwadratów i prostokątów.
Z kolei pierwiastek sześcienny odnosi się do liczby, która, podniesiona do potęgi 3, daje x. Na przykład, pierwiastek sześcienny z 27 to 3, ponieważ 3³ = 27. Pierwiastki sześcienne są często wykorzystywane w obliczeniach związanych z objętością brył, takich jak sześciany, co jest istotne w inżynierii i architekturze.
Pierwiastek kwadratowy: co to jest i jak go obliczyć?
Pierwiastek kwadratowy to liczba, która podniesiona do potęgi 2 daje określoną wartość. Na przykład, pierwiastek kwadratowy z 16 to 4, ponieważ 4² = 16. Obliczanie pierwiastków kwadratowych można przeprowadzić na kilka sposobów, w tym poprzez faktoryzację, korzystanie z kalkulatora lub metodę przybliżoną. W matematyce notacja pierwiastka kwadratowego zapisywana jest jako √a, gdzie a to liczba, z której chcemy wyznaczyć pierwiastek.
W praktyce, pierwiastki kwadratowe znajdują zastosowanie w wielu dziedzinach, takich jak geometria, gdzie są używane do obliczania długości boków kwadratów i prostokątów. Na przykład, jeśli pole kwadratu wynosi 25 m², to długość jego boku można obliczyć jako √25, co daje 5 m.
- Pole kwadratu: jeśli pole wynosi 36 m², długość boku to √36 = 6 m.
- Obliczenia w fizyce: pierwiastek kwadratowy jest używany przy obliczaniu prędkości i przyspieszenia.
- Statystyka: pierwiastki kwadratowe są wykorzystywane w obliczeniach odchyleń standardowych.
Pierwiastek sześcienny: definicja i przykłady zastosowania
Pierwiastek sześcienny to liczba, która podniesiona do potęgi 3 daje określoną wartość. Na przykład, pierwiastek sześcienny z 27 to 3, ponieważ 3³ = 27. Obliczanie pierwiastków sześciennych można przeprowadzić na podobnych zasadach jak w przypadku pierwiastków kwadratowych, ale z użyciem potęg trzecich. W notacji matematycznej pierwiastek sześcienny z liczby a zapisywany jest jako ∛a.
Pierwiastki sześcienne mają wiele zastosowań w inżynierii i architekturze, szczególnie przy obliczaniu objętości brył. Na przykład, jeśli objętość sześcianu wynosi 64 m³, to długość krawędzi można obliczyć jako ∛64, co daje 4 m. Takie obliczenia są istotne przy projektowaniu budynków i innych struktur.
Czytaj więcej: Nauka pisania lewą ręką: 5 skutecznych technik i ćwiczeń
Jak pierwiastki są używane w różnych dziedzinach matematyki?

Pierwiastki mają szerokie zastosowanie w matematyce, szczególnie w kontekście równań i funkcji. Wiele równań matematycznych wymaga obliczenia pierwiastków, aby znaleźć rozwiązania. Na przykład, w równaniach kwadratowych, pierwiastki są kluczowe do określenia miejsc zerowych funkcji. W praktyce, znajomość pierwiastków umożliwia rozwiązywanie złożonych problemów matematycznych oraz analizę różnych sytuacji w naukach ścisłych.
W kontekście funkcji, pierwiastki są używane do określenia wartości funkcji w punktach, które są istotne dla analizy. Na przykład, w funkcji kwadratowej, pierwiastki pozwalają na zrozumienie, w jakich punktach funkcja przecina oś X. To z kolei jest ważne w wielu zastosowaniach, od modelowania zjawisk fizycznych po rozwiązywanie problemów inżynieryjnych.
Zastosowanie pierwiastków w równaniach i funkcjach
Pierwiastki są kluczowym elementem w rozwiązywaniu równań matematycznych. Na przykład, w równaniu kwadratowym postaci ax² + bx + c = 0, aby znaleźć wartości x, które spełniają to równanie, trzeba obliczyć pierwiastki. Można to zrobić za pomocą wzoru kwadratowego, który zawiera pierwiastki: x = (-b ± √(b² - 4ac)) / 2a. Dzięki temu, pierwiastki pozwalają na znalezienie miejsc zerowych funkcji, co jest niezbędne w analizie matematycznej.Pierwiastki są również używane w funkcjach bardziej złożonych, takich jak funkcje trygonometryczne czy logarytmiczne. Na przykład, w funkcji logarytmicznej, pierwiastki mogą być używane do przekształcania równań w celu uproszczenia obliczeń. W ten sposób, pierwiastki stają się nie tylko narzędziem do rozwiązywania równań, ale również kluczem do zrozumienia bardziej skomplikowanych koncepcji matematycznych.
Pierwiastki w geometrii: jak wpływają na obliczenia?
Pierwiastki odgrywają istotną rolę w obliczeniach geometrycznych, szczególnie w kontekście obliczania powierzchni i objętości figur. Na przykład, aby obliczyć pole kwadratu, używamy wzoru A = a², gdzie a to długość boku. Aby znaleźć długość boku kwadratu, gdy znamy jego pole, musimy obliczyć pierwiastek kwadratowy z pola. To oznacza, że jeśli pole wynosi 36 m², długość boku kwadratu to √36, co daje 6 m. Takie obliczenia są kluczowe w architekturze i inżynierii, gdzie precyzyjne wymiary są niezbędne.
Pierwiastki są również używane do obliczania objętości brył, takich jak sześciany i prostopadłościany. Na przykład, aby obliczyć objętość sześcianu, używamy wzoru V = a³, gdzie a to długość krawędzi. Jeśli znamy objętość sześcianu, możemy obliczyć długość krawędzi, korzystając z pierwiastka sześciennego. Dlatego, jeśli objętość wynosi 64 m³, długość krawędzi to ∛64, co daje 4 m. Takie umiejętności są niezbędne w różnych dziedzinach, w tym w budownictwie i projektowaniu.
Wizualizacja pierwiastków: diagramy i przykłady
Wizualizacja pierwiastków jest kluczowa dla lepszego zrozumienia ich właściwości i zastosowań. Graficzne przedstawienia pierwiastków, takie jak wykresy funkcji y = √x oraz y = ∛x, pomagają zobaczyć, jak wartości pierwiastków zmieniają się w zależności od x. W przypadku pierwiastka kwadratowego, wykres jest parabolą, która rośnie od zera, natomiast wykres pierwiastka sześciennego ma formę krzywej, która przechodzi przez początek układu współrzędnych, co pokazuje, że pierwiastki sześcienne mogą być zarówno dodatnie, jak i ujemne.
Przykłady wizualizacji pierwiastków mogą obejmować wykresy funkcji oraz diagramy ilustrujące zastosowania pierwiastków w geometrii. Na przykład, można przedstawić wykresy pokazujące, jak zmienia się długość boku kwadratu w zależności od jego pola, lub jak zmienia się długość krawędzi sześcianu w zależności od jego objętości. Takie wizualizacje są niezwykle pomocne w nauczaniu matematyki i mogą ułatwić zrozumienie bardziej skomplikowanych koncepcji.
| Typ pierwiastka | Wykres |
| Pierwiastek kwadratowy |  |
| Pierwiastek sześcienny |  |
Jak pierwiastki wspierają nowoczesne technologie i inżynierię
Pierwiastki, choć często traktowane jako podstawowe pojęcia matematyczne, odgrywają kluczową rolę w nowoczesnych technologiach, takich jak komputery, programowanie i inżynieria danych. W obliczeniach związanych z algorytmami, które wykorzystują pierwiastki w analizie danych, inżynierowie mogą efektywniej modelować złożone systemy i przewidywać zachowania w różnych scenariuszach. Na przykład, w uczeniu maszynowym, pierwiastki są używane do normalizacji danych, co umożliwia lepsze wyniki w procesach klasyfikacji i regresji.W przyszłości, zastosowanie pierwiastków w technologiach takich jak sztuczna inteligencja i analiza big data będzie prawdopodobnie jeszcze bardziej rozwinięte. Zrozumienie i umiejętność manipulowania pierwiastkami mogą stać się kluczowe dla programistów i analityków, którzy będą musieli radzić sobie z coraz bardziej złożonymi obliczeniami. Takie umiejętności mogą również przyczynić się do innowacji w projektowaniu algorytmów, które wykorzystują pierwiastki do optymalizacji procesów i zwiększania efektywności operacyjnej w różnych branżach.