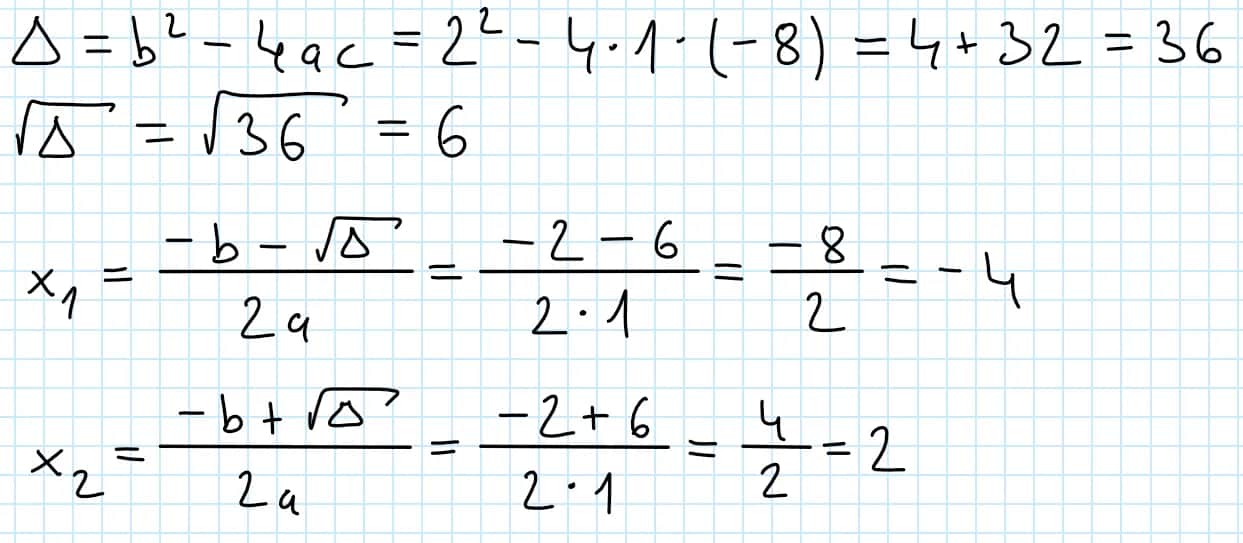Rozwiązywanie równań to kluczowa umiejętność w matematyce, która pozwala znaleźć liczbę, która spełnia dane równanie. Aby to zrobić, należy podstawić odpowiednią wartość w miejsce niewiadomej i sprawdzić, czy równanie jest prawdziwe. Właściwe zrozumienie tego procesu jest niezbędne, aby skutecznie rozwiązywać różnorodne równania, zarówno proste, jak i bardziej złożone.
W artykule omówimy, jak krok po kroku rozwiązywać równania oraz jak weryfikować, czy otrzymane rozwiązanie jest poprawne. Przedstawimy również różne typy równań oraz sposoby ich rozwiązywania. Dzięki tym informacjom, każdy czytelnik będzie mógł zyskać praktyczne umiejętności w zakresie rozwiązywania równań i ich weryfikacji.
Kluczowe wnioski:
- Aby rozwiązać równanie, trzeba znaleźć wartość, która spełnia równanie.
- Sprawdzenie poprawności rozwiązania polega na podstawieniu wartości do równania i porównaniu obu stron.
- Równania mogą mieć jedno, wiele lub żadne rozwiązanie, co wymaga indywidualnego podejścia do każdego przypadku.
- Przykłady równań pomagają w praktycznym zrozumieniu metod rozwiązywania i weryfikacji.
- Znajomość typów równań i ich rozwiązań jest kluczowa dla efektywnego rozwiązywania problemów matematycznych.
Jak rozwiązać równanie krok po kroku i znaleźć rozwiązanie
Rozwiązywanie równań to kluczowa umiejętność w matematyce, która pozwala znaleźć liczbę, która po podstawieniu w miejsce niewiadomej sprawia, że równanie staje się prawdziwe. Aby to zrobić, należy zrozumieć podstawowe pojęcia związane z równaniami, takie jak zmienne, stałe oraz równość. Proces ten jest nie tylko istotny w kontekście matematyki, ale także w codziennym życiu, gdzie często musimy podejmować decyzje na podstawie danych liczbowych.
Aby rozwiązać równanie, należy stosować różne metody w zależności od jego rodzaju. W pierwszym kroku warto zidentyfikować, z jakim typem równania mamy do czynienia. Następnie należy wykonać odpowiednie operacje matematyczne, aby wyizolować niewiadomą. Pamiętaj, że każda operacja powinna być wykonywana z zachowaniem równowagi równania, co oznacza, że jeśli coś dodasz do jednej strony, musisz to samo dodać do drugiej.
Zrozumienie podstawowych pojęć związanych z równaniami
Aby skutecznie rozwiązywać równania, należy najpierw zrozumieć kilka kluczowych terminów. Zmienne to symbole, które reprezentują nieznane wartości, podczas gdy stałe to liczby, które nie zmieniają się w trakcie rozwiązywania równania. Równość oznacza, że obie strony równania są sobie równe, co jest fundamentem każdej operacji matematycznej w tym procesie. Zrozumienie tych pojęć jest kluczowe dla dalszego rozwiązywania równań.
- Równania liniowe: to równania, w których najwyższym stopniem zmiennej jest 1, np. 2x + 3 = 7.
- Równania kwadratowe: to równania, w których najwyższym stopniem zmiennej jest 2, np. x² - 4x + 4 = 0.
- Równania sprzeczne: to równania, które nie mają rozwiązań, np. x + 2 = x - 3.
Metody rozwiązywania równań: od prostych do bardziej złożonych
Rozwiązywanie równań można przeprowadzać na wiele sposobów, w zależności od ich stopnia skomplikowania. Najprostsze metody obejmują operacje arytmetyczne, takie jak dodawanie, odejmowanie, mnożenie i dzielenie. Te podstawowe techniki są wystarczające w przypadku równań liniowych, gdzie niewiadoma występuje w pierwszym stopniu. Na przykład, aby rozwiązać równanie 3x + 5 = 20, wystarczy odjąć 5 od obu stron, a następnie podzielić przez 3, co prowadzi nas do rozwiązania x = 5.
- Operacje arytmetyczne: Używane w prostych równaniach liniowych, np. 2x + 3 = 7.
- Faktoryzacja: Technika stosowana w równaniach kwadratowych, np. x² - 5x + 6 = 0.
- Wzór kwadratowy: Używany do rozwiązywania równań kwadratowych w formie ax² + bx + c = 0.
Jak sprawdzić, czy rozwiązanie równania jest poprawne
Weryfikacja rozwiązania równania jest kluczowym krokiem w procesie rozwiązywania, który pozwala upewnić się, że uzyskana wartość rzeczywiście spełnia dane równanie. Aby to zrobić, należy podstawić otrzymaną wartość z powrotem do oryginalnego równania i obliczyć wartości obu stron. Jeśli lewa strona równania jest równa prawej stronie, to rozwiązanie jest poprawne. Na przykład, jeśli dla równania 2b + 13 = 41 obliczyliśmy, że b = 14, to po podstawieniu 14 do równania uzyskujemy 41, co potwierdza poprawność rozwiązania.
Weryfikacja jest szczególnie ważna w przypadku równań, które mogą mieć więcej niż jedno rozwiązanie lub w których występują złożone operacje. W takich przypadkach, sprawdzanie poprawności każdego rozwiązania pozwala uniknąć błędów i nieporozumień. Pamiętaj, że niektóre równania mogą być sprzeczne lub mieć nieskończoną liczbę rozwiązań, dlatego warto zawsze dokładnie sprawdzić, czy uzyskana liczba rzeczywiście spełnia równanie.
Proces weryfikacji rozwiązania krok po kroku
Aby zweryfikować rozwiązanie równania, należy postępować według kilku prostych kroków. Po pierwsze, podstaw wartość rozwiązania w miejsce niewiadomej w równaniu. Następnie oblicz wartość lewej i prawej strony równania. Jeśli obie strony są równe, to rozwiązanie jest poprawne. Na przykład, dla równania 3x - 5 = 10, jeśli x = 5, po podstawieniu uzyskujemy 3(5) - 5 = 15 - 5 = 10, co potwierdza, że x = 5 jest poprawnym rozwiązaniem.
| Rodzaj weryfikacji | Przykład | Wynik |
|---|---|---|
| Poprawna weryfikacja | 2b + 13 = 41, b = 14 | 41 = 41 (poprawne) |
| Niepoprawna weryfikacja | 2b + 13 = 41, b = 10 | 33 ≠ 41 (niepoprawne) |
Częste błędy przy sprawdzaniu poprawności rozwiązania
Podczas weryfikacji rozwiązania równania, wiele osób popełnia typowe błędy, które mogą prowadzić do błędnych wniosków. Jednym z najczęstszych błędów jest niedokładne obliczenie wartości lewej lub prawej strony równania, co może wynikać z pośpiechu lub braku uwagi. Innym problemem jest nieprawidłowe podstawienie wartości do równania, co prowadzi do błędnych wyników. Często zdarza się również, że użytkownicy mylą znaki operacji matematycznych, co może całkowicie zmienić wynik. Aby uniknąć tych błędów, warto zawsze dokładnie sprawdzić każdy krok w procesie weryfikacji.

Różne typy równań i ich rozwiązania: co musisz wiedzieć
Równania można podzielić na różne typy, w zależności od ich struktury i stopnia. Równania liniowe to najprostsza forma, gdzie najwyższy stopień zmiennej wynosi 1. Przykładem może być równanie 2x + 3 = 7, które można łatwo rozwiązać poprzez prostą manipulację algebraiczną. Równania kwadratowe, z najwyższym stopniem wynoszącym 2, są bardziej złożone i wymagają zastosowania różnych metod, takich jak faktoryzacja czy wzór kwadratowy. Przykład równania kwadratowego to x² - 5x + 6 = 0, które można rozwiązać na kilka sposobów.
Inne typy równań obejmują równania sprzeczne, które nie mają rozwiązań, oraz równania tożsamościowe, które są prawdziwe dla wszystkich wartości zmiennej. Na przykład, równanie 2x + 4 = 2(x + 2) jest równaniem tożsamościowym, ponieważ obie strony są zawsze równe. Zrozumienie tych różnych typów równań jest kluczowe dla efektywnego rozwiązywania problemów matematycznych i umiejętności ich weryfikacji.
Równania z jednym, wieloma i brakiem rozwiązań
Równania mogą mieć różne typy rozwiązań, co jest kluczowe do zrozumienia ich natury. Równania z jednym rozwiązaniem to takie, w których istnieje dokładnie jedna wartość zmiennej, która spełnia równanie. Na przykład, równanie 2x + 4 = 10 ma jedno rozwiązanie: x = 3. Z kolei równania z wieloma rozwiązaniami występują, gdy zmienna może przyjmować więcej niż jedną wartość. Na przykład, równanie x² = 9 ma dwa rozwiązania: x = 3 oraz x = -3. Istnieją również równania, które nie mają rozwiązań, zwane równaniami sprzecznymi. Przykładem takiego równania jest 2x + 1 = 2x - 3, które nie ma rozwiązań, ponieważ po przekształceniach dochodzimy do sprzeczności 1 = -3.
- Równania z jednym rozwiązaniem: np. 3x - 5 = 10, gdzie x = 5.
- Równania z wieloma rozwiązaniami: np. x² - 4 = 0, gdzie x = 2 i x = -2.
- Równania sprzeczne: np. x + 2 = x - 3, które nie ma rozwiązań.
Przykłady równań do samodzielnego rozwiązania i weryfikacji
Teraz, aby praktycznie zastosować zdobytą wiedzę, zachęcamy do samodzielnego rozwiązania poniższych równań. Użyj różnych metod, które poznaliście wcześniej, aby znaleźć rozwiązania i sprawdzić ich poprawność. To doskonała okazja, aby przećwiczyć swoje umiejętności i upewnić się, że rozumiesz, jak rozwiązać równanie i sprawdzić, czy otrzymana liczba spełnia to równanie.
Jak wykorzystać równania w codziennym życiu i pracy
Równania nie są tylko teoretycznym zagadnieniem matematycznym; mają również praktyczne zastosowanie w codziennym życiu oraz w różnych dziedzinach zawodowych. Na przykład, w finansach osobistych równania mogą pomóc w obliczaniu odsetek kredytów, planowaniu budżetu czy analizie oszczędności. Dzięki umiejętności rozwiązywania równań, można lepiej zrozumieć, jak różne czynniki wpływają na nasze finanse, co umożliwia podejmowanie bardziej świadomych decyzji.
W nauce i inżynierii równania są kluczowe do modelowania różnych zjawisk, od ruchu pojazdów po reakcje chemiczne. Zrozumienie, jak stosować równania w praktycznych sytuacjach, otwiera drzwi do innowacji i rozwoju technologii. Przykładowo, inżynierowie wykorzystują równania do obliczania sił działających na konstrukcje, co jest niezbędne dla zapewnienia ich bezpieczeństwa i stabilności. Warto więc rozwijać umiejętności związane z równaniami, aby lepiej przygotować się na wyzwania, które mogą pojawić się w przyszłości.