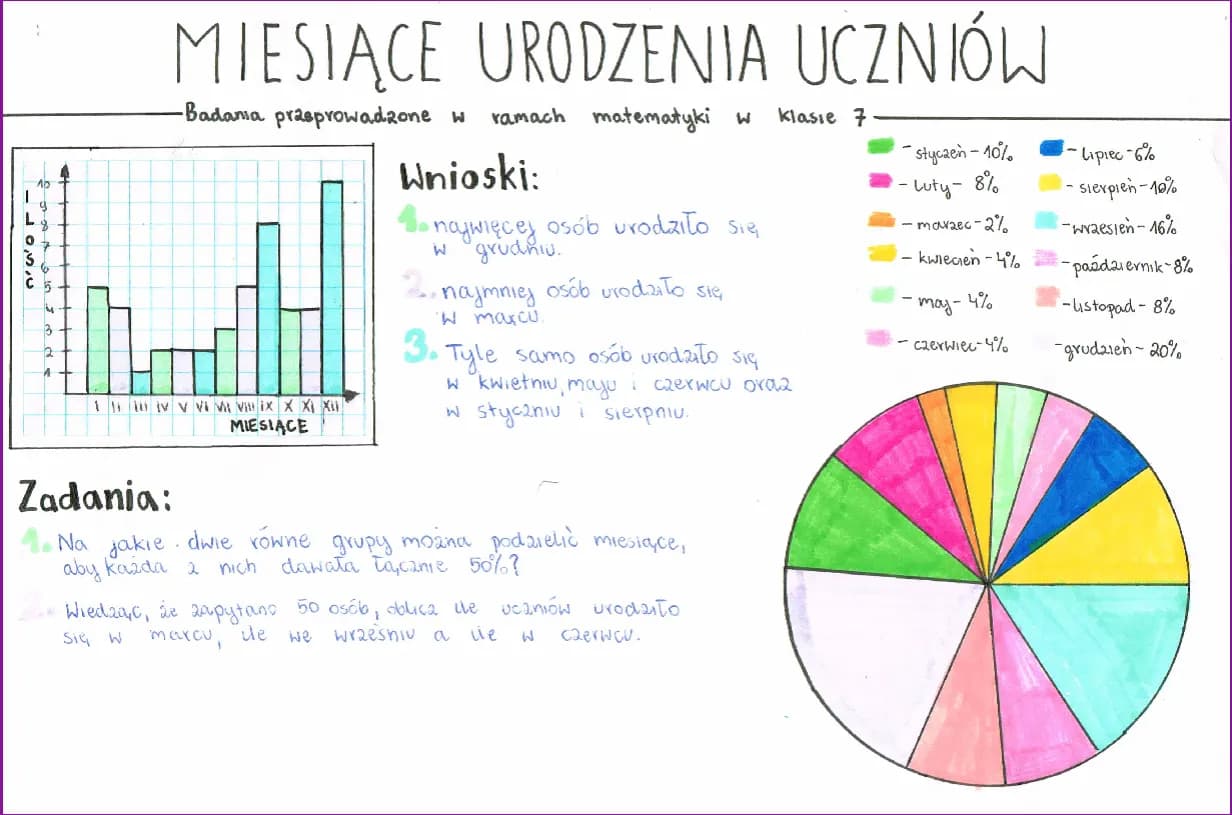
Statystyka matematyczna to kluczowy dział statystyki, który łączy teorię prawdopodobieństwa z innymi dziedzinami matematyki, aby rozwijać metody wnioskowania statystycznego. Zajmuje się analizą danych dotyczących zjawisk losowych, które są często opisywane za pomocą modeli probabilistycznych. Głównym celem statystyki matematycznej jest wyciąganie wniosków o całej populacji na podstawie wyników uzyskanych z próby. W tym kontekście stosuje się różnorodne metody, takie jak estymacja parametrów rozkładu oraz weryfikacja hipotez statystycznych.
Wartości statystyczne, takie jak średnia arytmetyczna, mediana czy odchylenie standardowe, są przykładami wskaźników, które można analizować w ramach tej dziedziny. Statystyka matematyczna nie tylko dostarcza teoretycznych podstaw dla metod stosowanych w statystyce stosowanej, ale także umożliwia zrozumienie złożonych procesów zachodzących w naturze i społeczeństwie.
Najistotniejsze informacje:
- Statystyka matematyczna wykorzystuje teorię prawdopodobieństwa do analizy danych zjawisk losowych.
- Jej celem jest wyciąganie wniosków o populacji na podstawie prób.
- Stosowane metody obejmują estymację parametrów i weryfikację hipotez statystycznych.
- Wskaźniki takie jak średnia, mediana i odchylenie standardowe są kluczowe w analizie danych.
- Statystyka matematyczna stanowi fundament dla statystyki stosowanej, umożliwiając zrozumienie złożonych procesów.
Definicja statystyki w matematyce i jej znaczenie w analizie danych
Statystyka w matematyce to dział zajmujący się analizą danych oraz interpretacją wyników zjawisk losowych. Jej podstawowym celem jest wyciąganie wniosków o całej populacji na podstawie danych uzyskanych z próby. Statystyka wykorzystuje różnorodne metody, które pozwalają na zrozumienie i opisanie zjawisk w sposób matematyczny, co jest kluczowe w podejmowaniu decyzji opartych na danych.
W kontekście analizy danych, statystyka odgrywa fundamentalną rolę w różnych dziedzinach, takich jak nauki przyrodnicze, społeczne czy ekonomiczne. Dzięki zastosowaniu teorii prawdopodobieństwa oraz innych narzędzi matematycznych, statystyka umożliwia efektywne modelowanie i przewidywanie zachowań populacji, co jest nieocenione w badaniach naukowych i praktyce biznesowej.
Kluczowe pojęcia: co to jest statystyka i jej elementy
W statystyce wyróżniamy dwa główne obszary: statystykę opisową i statystykę inferencyjną. Statystyka opisowa skupia się na zbieraniu, organizowaniu i prezentowaniu danych w sposób przystępny. Używa różnych wskaźników, takich jak średnia arytmetyczna, mediana czy odchylenie standardowe, aby opisać właściwości zbioru danych. Dzięki tym wskaźnikom można szybko zrozumieć podstawowe cechy danych, co ułatwia ich analizę.
Z kolei statystyka inferencyjna zajmuje się wyciąganiem wniosków o populacji na podstawie danych z próby. Umożliwia to oszacowanie parametrów, takich jak średnie czy proporcje, oraz testowanie hipotez statystycznych. Wykorzystując metody inferencyjne, badacze mogą ocenić, na ile wyniki uzyskane w próbie są reprezentatywne dla całej populacji. To podejście jest kluczowe w wielu badaniach, gdzie pełne dane o populacji są trudne lub niemożliwe do zdobycia.
Rola statystyki w podejmowaniu decyzji opartych na danych
Statystyka odgrywa kluczową rolę w podejmowaniu decyzji opartych na danych, wpływając na sposób, w jaki organizacje i jednostki analizują informacje i podejmują działania. Dzięki zastosowaniu statystyki, można lepiej zrozumieć złożone zjawiska i wyciągać trafne wnioski, co jest szczególnie istotne w dzisiejszym świecie, gdzie dane są na wyciągnięcie ręki. Właściwe wykorzystanie danych statystycznych pozwala na optymalizację procesów oraz podejmowanie bardziej świadomych decyzji w różnych dziedzinach, takich jak biznes, medycyna czy nauka.
Zastosowanie teorii prawdopodobieństwa w statystyce matematycznej
Teoria prawdopodobieństwa jest fundamentem, na którym opiera się statystyka matematyczna. Umożliwia ona modelowanie zjawisk losowych oraz analizę danych w sposób matematyczny. Dzięki teorii prawdopodobieństwa, statystyka może dostarczać narzędzi do oszacowania ryzyka i przewidywania przyszłych zdarzeń, co jest nieocenione w wielu dziedzinach, od finansów po nauki przyrodnicze. Zrozumienie tej relacji jest kluczowe dla skutecznego stosowania metod statystycznych w praktyce.
Jak prawdopodobieństwo wpływa na analizy statystyczne
Prawdopodobieństwo jest kluczowym elementem, który wpływa na analizy statystyczne. Umożliwia ono zrozumienie i modelowanie zjawisk losowych, które są istotne w statystyce. Dzięki koncepcji zmiennych losowych, statystyka może opisywać różne wyniki i ich prawdopodobieństwa, co jest niezbędne do podejmowania decyzji na podstawie danych. Na przykład, rozkład prawdopodobieństwa pozwala na określenie, jakie są szanse na wystąpienie określonego wyniku w danej próbie.
W analizach statystycznych, prawdopodobieństwo wpływa również na interpretację wyników. Umożliwia to ocenę, na ile wyniki uzyskane w próbie mogą być reprezentatywne dla całej populacji. Wykorzystując różne rozkłady, takie jak rozkład normalny czy rozkład Poissona, analitycy mogą lepiej zrozumieć struktury danych i ich zachowanie. Takie podejście jest nieocenione w badaniach, gdzie zrozumienie ryzyka i niepewności jest kluczowe dla uzyskania wiarygodnych wyników.
Przykłady zastosowań teorii prawdopodobieństwa w praktyce
Teoria prawdopodobieństwa znajduje zastosowanie w wielu dziedzinach, co pozwala na skuteczne podejmowanie decyzji na podstawie danych. Przykłady obejmują kontrolę jakości w produkcji, gdzie prawdopodobieństwo wystąpienia wadliwych produktów jest analizowane, a także ocenę ryzyka w finansach, gdzie modele probabilistyczne pomagają przewidzieć zmiany na rynkach. W medycynie, prawdopodobieństwo jest używane do oceny skuteczności leczenia i przewidywania wyników zdrowotnych pacjentów.
| Branża | Zastosowanie teorii prawdopodobieństwa |
| Produkcja | Analiza wadliwości produktów w kontrolach jakości |
| Finanse | Ocena ryzyka inwestycyjnego i przewidywanie trendów rynkowych |
| Medycyna | Ocena skuteczności terapii i przewidywanie wyników zdrowotnych |
Metody wnioskowania statystycznego i ich znaczenie
Wnioskowanie statystyczne to proces, który pozwala na wyciąganie wniosków o populacji na podstawie danych z próby. Kluczowymi metodami wnioskowania są estymacja oraz testowanie hipotez. Estymacja polega na szacowaniu parametrów populacji, takich jak średnia czy proporcje, na podstawie wyników uzyskanych z próby. Testowanie hipotez z kolei umożliwia ocenę, czy dane obserwacje są zgodne z określoną hipotezą, co jest istotne w wielu badaniach naukowych i praktycznych zastosowaniach.
Rodzaje wnioskowania: estymacja i testowanie hipotez
Estymacja jest jednym z fundamentalnych elementów wnioskowania statystycznego. Polega na określeniu wartości parametrów populacji na podstawie danych z próby. Wyróżniamy estymację punktową, która podaje pojedynczą wartość jako szacowaną, oraz estymację przedziałową, która określa zakres wartości, w którym z dużym prawdopodobieństwem znajduje się szacowany parametr. Tego rodzaju analiza jest niezbędna, aby zrozumieć, jak wyniki z próby mogą odnosić się do całej populacji.
Testowanie hipotez to kolejna kluczowa metoda wnioskowania statystycznego. Polega na formułowaniu hipotezy zerowej (H0) i alternatywnej (H1), a następnie ocenianiu, czy dane z próby dostarczają wystarczających dowodów, aby odrzucić hipotezę zerową. Proces ten obejmuje obliczenie statystyki testowej i porównanie jej z wartością krytyczną, co pozwala na podjęcie decyzji o akceptacji lub odrzuceniu hipotezy. Testowanie hipotez jest szeroko stosowane w badaniach naukowych, aby potwierdzić lub obalić teorie na podstawie zgromadzonych danych.
Praktyczne zastosowania wnioskowania w różnych dziedzinach
Wnioskowanie statystyczne znajduje zastosowanie w wielu dziedzinach, co pozwala na podejmowanie świadomych decyzji opartych na danych. Na przykład w zdrowiu publicznym analizy statystyczne pomagają w ocenie skuteczności nowych leków oraz w badaniu rozprzestrzenienia chorób. W marketingu, firmy wykorzystują metody wnioskowania do analizy zachowań klientów, co pozwala na lepsze dostosowanie ofert do potrzeb rynku. W edukacji natomiast, wnioskowanie statystyczne jest używane do oceny wyników uczniów oraz skuteczności różnych metod nauczania.
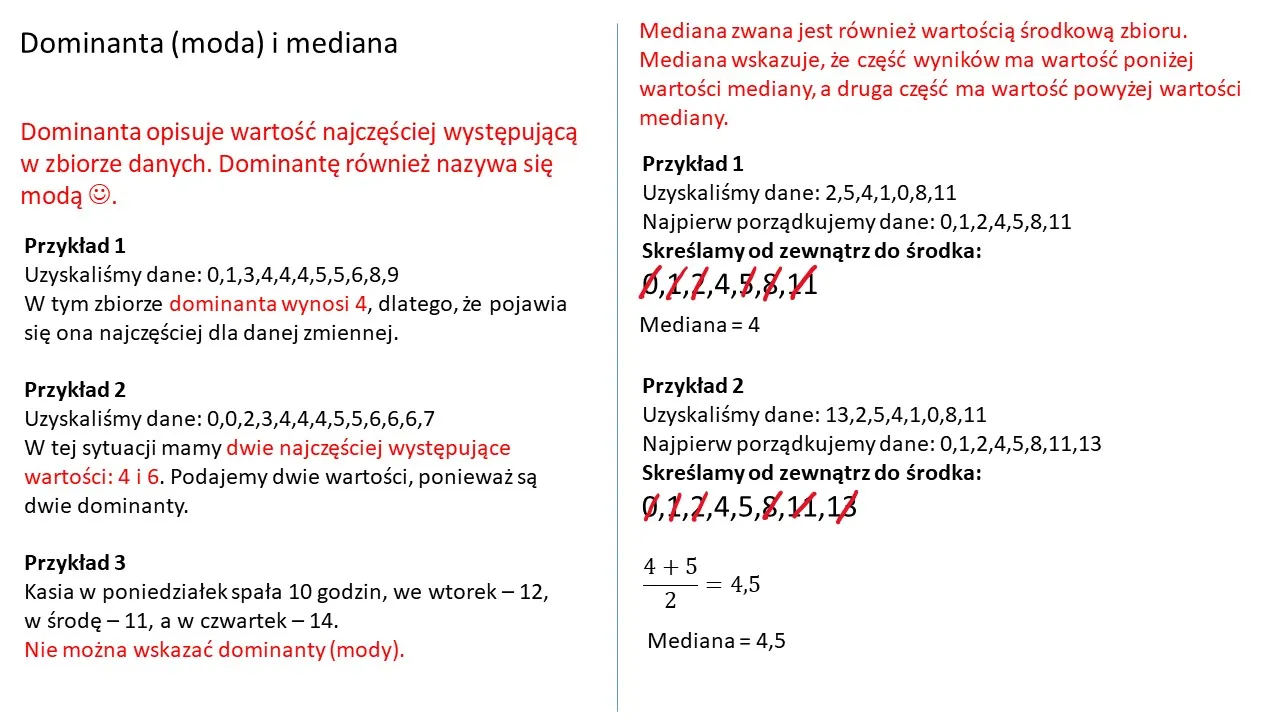
Analiza danych: techniki i narzędzia statystyczne
Analiza danych obejmuje różnorodne techniki i narzędzia statystyczne, które umożliwiają wydobycie wartościowych informacji z zebranych danych. Wśród najpopularniejszych metod znajdują się zarówno statystyka opisowa, która koncentruje się na podsumowywaniu danych, jak i statystyka inferencyjna, która pozwala na wyciąganie wniosków o populacji na podstawie próby. Wykorzystując odpowiednie narzędzia, takie jak programy statystyczne, analitycy mogą skutecznie przetwarzać i interpretować dane, co jest kluczowe dla podejmowania decyzji w różnych dziedzinach.
Jak wykorzystać analizy statystyczne w prognozowaniu trendów
Analizy statystyczne mogą być nieocenionym narzędziem w prognozowaniu trendów, co pozwala na lepsze planowanie i podejmowanie decyzji strategicznych. Wykorzystując metody takie jak regresja liniowa czy analiza szeregów czasowych, organizacje mogą przewidywać przyszłe zachowania klientów, zmiany na rynku oraz inne istotne zjawiska. Przykładowo, w branży retail, analiza danych sprzedażowych z poprzednich sezonów może pomóc w przewidywaniu popytu na konkretne produkty, co z kolei pozwala na efektywne zarządzanie zapasami i optymalizację działań marketingowych.
W przyszłości, rozwój technologii, takich jak sztuczna inteligencja i uczenie maszynowe, może jeszcze bardziej wzbogacić możliwości analiz statystycznych. Dzięki tym technologiom, firmy będą mogły nie tylko analizować dane w czasie rzeczywistym, ale także automatycznie dostosowywać swoje strategie na podstawie wykrytych wzorców i anomalii. Zastosowanie tych zaawansowanych technik w wnioskowaniu statystycznym otworzy nowe horyzonty dla organizacji, umożliwiając im szybsze i bardziej precyzyjne reagowanie na zmieniające się warunki rynkowe.