Obliczanie wysokości w trójkącie równoramiennym może wydawać się skomplikowane, ale w rzeczywistości jest to prosty proces, który można zrozumieć dzięki odpowiedniemu wzorowi. Wysokość trójkąta równoramiennego jest kluczowym elementem, który pozwala na dokładne określenie jego powierzchni oraz innych właściwości geometrycznych. W tym artykule przedstawimy łatwe metody obliczania wysokości oraz praktyczne przykłady, które pomogą w lepszym zrozumieniu tego zagadnienia.
Wysokość trójkąta równoramiennego można obliczyć za pomocą wzoru, który uwzględnia długość podstawy oraz długość ramienia. Zrozumienie tego wzoru oraz jego zastosowanie w praktyce jest kluczowe dla każdego, kto chce zgłębić temat geometrii. Dzięki prostym obliczeniom oraz wizualizacjom, każdy będzie mógł samodzielnie obliczyć wysokość trójkąta równoramiennego.
Kluczowe wnioski:- Wysokość trójkąta równoramiennego można obliczyć za pomocą wzoru: h = √(b² - (a/2)²), gdzie h to wysokość, a to długość podstawy, a b to długość ramienia.
- Wzór ten pozwala na szybkie i dokładne obliczenia, co jest przydatne w różnych zadaniach matematycznych.
- Warto znać różne jednostki miary, ponieważ wysokość może być obliczana w centymetrach, metrach lub innych jednostkach.
- Diagramy i wizualizacje są pomocne w zrozumieniu, jak zmiany długości boków wpływają na wysokość trójkąta.
- Unikanie typowych błędów w obliczeniach jest kluczowe dla uzyskania poprawnych wyników, dlatego warto znać najczęstsze pułapki.
Jak obliczyć wysokość w trójkącie równoramiennym - podstawowe informacje
Trójkąt równoramienny to figura geometryczna, która ma dwie równe boki oraz kąty przy podstawie o tej samej miarze. Wysokość trójkąta równoramiennego jest kluczowym parametrem, który pozwala na dokładne obliczenie jego powierzchni oraz zrozumienie jego właściwości. Znalezienie wysokości jest istotne nie tylko w geometrii, ale także w zastosowaniach praktycznych, takich jak architektura czy inżynieria.
Aby obliczyć wysokość w trójkącie równoramiennym, używamy specjalnego wzoru, który uwzględnia długości boków. Wzór ten jest prosty i skuteczny, a jego znajomość pozwala na szybkie obliczenia. Wysokość trójkąta jest oznaczana literą h i oblicza się ją na podstawie długości podstawy a oraz długości ramienia b. W kolejnych częściach artykułu przyjrzymy się szczegółowo, jak korzystać z tego wzoru i jakie są jego zastosowania.
Zrozumienie trójkąta równoramiennego i jego właściwości
Trójkąt równoramienny charakteryzuje się tym, że dwa jego boki są równe, co wpływa na jego symetrię. Kąty przy podstawie są również równe, co oznacza, że trójkąt ten jest symetryczny względem linii wysokości, która dzieli go na dwa mniejsze trójkąty prostokątne. Wysokość trójkąta równoramiennego jest odcinkiem, który łączy wierzchołek trójkąta z podstawą, tworząc kąt prosty. Dzięki tym właściwościom, obliczanie wysokości staje się bardziej intuicyjne.
Wzór na wysokość trójkąta równoramiennego - krok po kroku
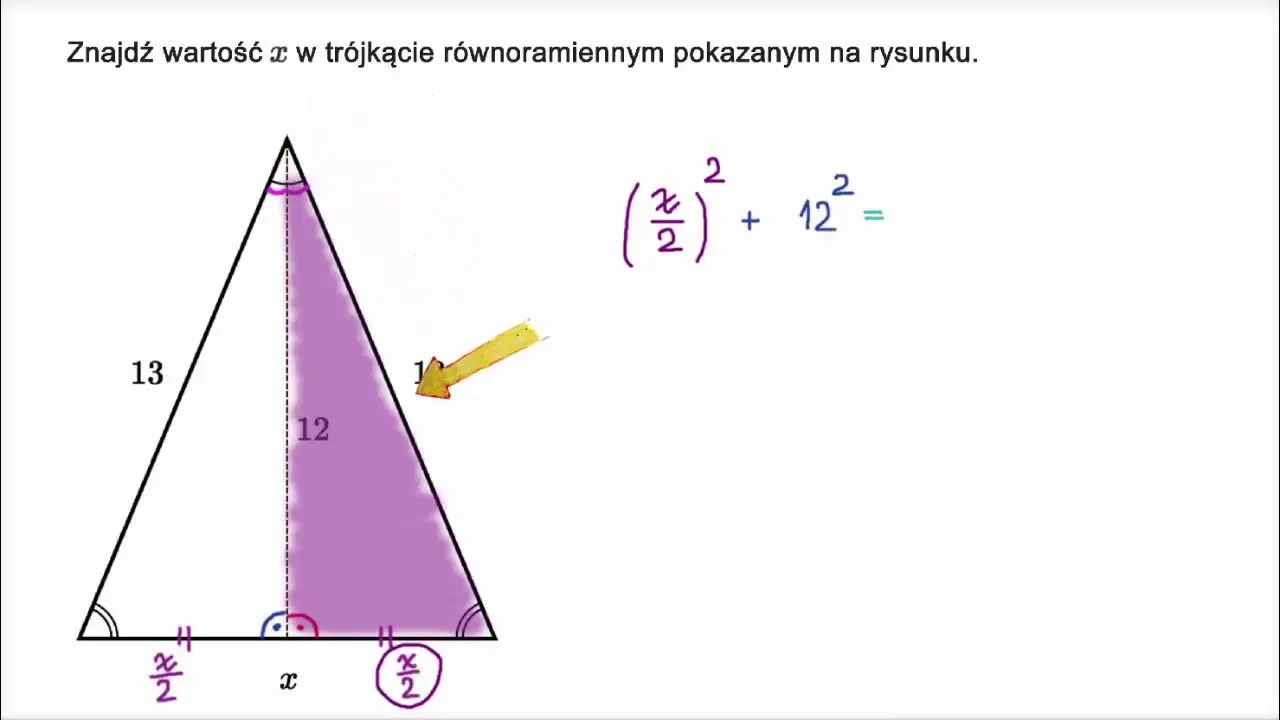
Aby obliczyć wysokość w trójkącie równoramiennym, stosujemy wzór: h = √(b² - (a/2)²). W tym wzorze h oznacza wysokość, a to długość podstawy, a b to długość ramienia. Wzór ten działa na zasadzie twierdzenia Pitagorasa, gdzie wysokość jest przeciwprostokątną w utworzonym trójkącie prostokątnym. Aby poprawnie użyć wzoru, należy najpierw podzielić długość podstawy przez dwa, a następnie obliczyć różnicę między kwadratem długości ramienia a kwadratem połowy podstawy. Na koniec bierzemy pierwiastek kwadratowy z uzyskanej wartości, co daje nam wysokość trójkąta.
| Symbol | Opis |
| h | Wysokość trójkąta |
| a | Długość podstawy |
| b | Długość ramienia |
Przykłady obliczeń wysokości w trójkącie równoramiennym
Obliczanie wysokości w trójkącie równoramiennym jest kluczowe w wielu zastosowaniach, od geometrii po inżynierię. Aby obliczyć wysokość, należy znać długości podstawy oraz ramion trójkąta. Na przykład, jeśli podstawa trójkąta wynosi 8 cm, a długość ramienia 5 cm, można zastosować wzór, który wcześniej omówiliśmy. Wykonując obliczenia, otrzymujemy wysokość wynoszącą 4,8 cm, co można uzyskać poprzez podstawienie wartości do wzoru: h = √(5² - (8/2)²).
Warto również zauważyć, że wysokość trójkąta równoramiennego można obliczyć w różnych jednostkach miary. Na przykład, obliczając wysokość w centymetrach, możemy przeliczyć wynik na metry lub cale, co jest przydatne w praktycznych zastosowaniach. Pamiętaj, aby zawsze dostosować jednostki do kontekstu, w którym pracujesz, aby uniknąć błędów w obliczeniach. Dzięki temu, każdy będzie mógł łatwo przeliczać wartości i uzyskiwać poprawne wyniki.
Obliczanie wysokości na podstawie długości podstawy i ramion
Załóżmy, że mamy trójkąt równoramienny z podstawą o długości 10 cm i ramionami długości 7 cm. Aby obliczyć wysokość, używamy wzoru: h = √(b² - (a/2)²). W tym przypadku, podstawiając wartości, obliczamy: h = √(7² - (10/2)²) = √(49 - 25) = √24 ≈ 4,9 cm. W ten sposób uzyskujemy wysokość trójkąta równoramiennego, co jest niezwykle przydatne w dalszych obliczeniach dotyczących powierzchni lub innych właściwości.
- Długość podstawy: 10 cm, długość ramion: 7 cm, wysokość: 4,9 cm
- Długość podstawy: 6 cm, długość ramion: 5 cm, wysokość: 4,0 cm
- Długość podstawy: 12 cm, długość ramion: 8 cm, wysokość: 6,0 cm
Wysokość trójkąta równoramiennego z użyciem różnych jednostek
Obliczanie wysokości trójkąta równoramiennego może być wykonane w różnych jednostkach miary, takich jak centymetry, metry czy cale. Ważne jest, aby upewnić się, że wszystkie wymiary są podane w tych samych jednostkach przed przystąpieniem do obliczeń. Na przykład, jeśli długość podstawy wynosi 100 cm i długość ramienia 70 cm, to wysokość można obliczyć w centymetrach. Jeśli jednak chcemy uzyskać wysokość w metrach, musimy pamiętać o przeliczeniu jednostek, co może wpłynąć na końcowy wynik.
Konwersja jednostek jest kluczowa, ponieważ błędy w tym zakresie mogą prowadzić do niepoprawnych wyników. Na przykład, przeliczając 100 cm na metry, otrzymujemy 1 m, a wówczas obliczenia muszą być dostosowane do nowego formatu. Używając wzoru, który już znasz, można łatwo obliczyć wysokość w różnych jednostkach, co jest przydatne w praktycznych zastosowaniach, takich jak budownictwo czy projektowanie.
Czytaj więcej: Kto może prowadzić zajęcia rewalidacyjne? Kluczowe kwalifikacje
Diagramy i wizualizacje - jak lepiej zrozumieć wysokość trójkąta
Wizualizacje i diagramy są niezwykle pomocne w zrozumieniu koncepcji wysokości trójkąta równoramiennego. Dzięki nim można zobaczyć, jak wysokość dzieli trójkąt na dwa mniejsze, równe trójkąty prostokątne. Takie przedstawienie graficzne ułatwia dostrzeganie relacji między bokami oraz kątami, co jest istotne dla lepszego przyswojenia materiału. Warto korzystać z narzędzi graficznych, aby stworzyć czytelne diagramy, które będą obrazować wszystkie istotne elementy.
Tworzenie diagramów nie tylko ułatwia zrozumienie, ale również pozwala na lepsze zapamiętanie wzorów i właściwości trójkątów. Można na przykład narysować trójkąt równoramienny i zaznaczyć jego wysokość, co pomoże w identyfikacji kluczowych elementów. Takie wizualizacje są szczególnie przydatne dla uczniów i studentów, którzy uczą się geometrii i chcą lepiej zrozumieć teoretyczne zagadnienia w praktyce.
Tworzenie diagramu trójkąta równoramiennego z wysokością
Aby stworzyć diagram trójkąta równoramiennego z oznaczoną wysokością, należy zacząć od narysowania podstawy trójkąta. Wybierz długość podstawy, na przykład 10 cm, i zaznacz dwa końce, które będą punktami A i B. Następnie, aby znaleźć wierzchołek C, musisz określić długość ramion trójkąta, na przykład 7 cm. Użyj cyrkla, aby z jednego z końców podstawy (punktu A) narysować okrąg o promieniu równym długości ramienia. Powtórz tę czynność z punktu B.
W miejscu, gdzie okręgi się przecinają, znajduje się wierzchołek C. Po narysowaniu linii od punktu C do punktów A i B, możesz teraz zaznaczyć wysokość trójkąta. Wysokość (odcinek CD) to linia prosta, która łączy wierzchołek C z podstawą AB, tworząc kąt prosty. Oznacz ten odcinek jako wysokość h. Taki diagram nie tylko ułatwia zrozumienie geometrii trójkąta równoramiennego, ale również pozwala lepiej zobrazować, jak oblicza się wysokość w praktyce.
Analiza wpływu zmian długości boków na wysokość
Zmiana długości boków trójkąta równoramiennego ma bezpośredni wpływ na jego wysokość. Na przykład, jeśli zwiększysz długość ramion przy stałej długości podstawy, wysokość trójkąta wzrośnie. Z drugiej strony, skracając długość ramion, wysokość również się zmniejszy. To zjawisko można zrozumieć, analizując wzór na wysokość, który uwzględnia długości boków. Warto również zauważyć, że przy stałej długości ramion, zmiana długości podstawy wpłynie na wysokość, ponieważ wysokość jest powiązana z różnicą między długościami boków a długością podstawy.
Przykładowo, trójkąt o podstawie 10 cm i ramionach 8 cm będzie miał inną wysokość niż trójkąt o podstawie 10 cm i ramionach 6 cm. Dlatego ważne jest, aby podczas obliczeń wysokości brać pod uwagę wszystkie zmienne, aby uzyskać dokładne wyniki. Analizując te zmiany, można lepiej zrozumieć, jak geometria wpływa na różne właściwości trójkątów równoramiennych.
Typowe błędy w obliczeniach wysokości trójkąta równoramiennego
Podczas obliczania wysokości w trójkącie równoramiennym, wiele osób popełnia typowe błędy, które mogą prowadzić do niepoprawnych wyników. Jednym z najczęstszych błędów jest niewłaściwe stosowanie wzoru. Użytkownicy często mylą długości boków lub pomijają ważne kroki, takie jak dzielenie długości podstawy przez dwa przed przystąpieniem do obliczeń. Innym problemem jest nieprawidłowe przeliczanie jednostek, co może znacząco wpłynąć na ostateczny wynik. Dlatego kluczowe jest, aby zwracać uwagę na każdy szczegół podczas wykonywania obliczeń.
Innym powszechnym błędem jest pomijanie sprawdzenia wyników. Po obliczeniach warto zawsze zweryfikować, czy uzyskana wysokość jest logiczna w kontekście długości boków trójkąta. Na przykład, jeśli wysokość wydaje się być większa od długości ramion, na pewno coś poszło nie tak. Aby uniknąć tych pułapek, ważne jest, aby każdy krok obliczeń był dokładnie przemyślany i sprawdzony.
Najczęstsze pułapki przy stosowaniu wzoru
Podczas korzystania z wzoru na wysokość trójkąta równoramiennego, użytkownicy często napotykają na różne pułapki. Jedną z nich jest niewłaściwe zrozumienie, jak obliczyć kwadrat długości ramienia oraz połowy długości podstawy. Błędne podstawienie wartości do wzoru może prowadzić do całkowicie błędnych wyników. Innym problemem jest pomijanie pierwiastkowania, co jest kluczowym krokiem w uzyskaniu wysokości. Upewnij się, że każdy etap jest dokładnie wykonany, aby uniknąć takich pomyłek.
Jak unikać błędów w zadaniach matematycznych dotyczących wysokości
Aby unikać błędów w obliczeniach wysokości trójkąta równoramiennego, warto stosować kilka praktycznych strategii. Przede wszystkim, zawsze podwójnie sprawdzaj swoje obliczenia i upewnij się, że wszystkie jednostki są zgodne. Możesz również zapisać każdy krok obliczeń, co pomoże w identyfikacji potencjalnych błędów. Dodatkowo, korzystanie z diagramów i wizualizacji może pomóc w lepszym zrozumieniu problemu i uniknięciu pomyłek. Regularne ćwiczenie z różnymi wymiarami trójkątów również zwiększy pewność siebie i umiejętność obliczeń.
Jak wykorzystać wysokość trójkąta równoramiennego w praktyce
Wysokość trójkąta równoramiennego ma istotne zastosowanie nie tylko w matematyce, ale także w wielu dziedzinach inżynierii i architektury. Na przykład, w projektowaniu budynków, zrozumienie, jak obliczyć wysokość trójkąta, może pomóc w tworzeniu stabilnych konstrukcji dachowych. Wysokość trójkąta jest kluczowa przy obliczaniu kątów nachylenia dachu, co wpływa na efektywność odprowadzania wody deszczowej oraz ogólną trwałość budynku. Wykorzystując wzór na wysokość, inżynierowie mogą precyzyjnie określić, jakie materiały będą potrzebne oraz jakie obciążenia konstrukcja będzie w stanie wytrzymać.
Dodatkowo, w zastosowaniach artystycznych, takich jak rzeźba czy malarstwo, znajomość wysokości trójkąta równoramiennego może wspierać artystów w tworzeniu harmonijnych kompozycji. Zrozumienie proporcji i symetrii, które wynikają z wysokości, pozwala na lepsze planowanie dzieł, które są nie tylko estetyczne, ale także technicznie poprawne. W ten sposób, umiejętność obliczania wysokości trójkąta równoramiennego może być narzędziem do osiągania sukcesów w różnych dziedzinach, od inżynierii po sztukę.
