Zwrot wektora w fizyce to kluczowy element, który odgrywa istotną rolę w zrozumieniu wektorów. Określa on, w którą stronę wskazuje wektor, co ma ogromne znaczenie w analizie ruchu oraz w różnych zastosowaniach fizycznych. Wektory są nie tylko matematycznymi narzędziami, ale także pomagają w opisie rzeczywistych zjawisk, takich jak siły, prędkości czy przyspieszenia.
W tym artykule przyjrzymy się, czym dokładnie jest zwrot wektora, jak wpływa na analizę wektorów oraz jakie są jego właściwości. Zrozumienie zwrotu jest niezbędne, aby skutecznie posługiwać się wektorami w fizyce i w codziennym życiu.
Kluczowe wnioski:- Zwrot wektora określa kierunek, w którym wskazuje strzałka wektora.
- Dwa wektory mają ten sam zwrot, gdy są skierowane w tę samą stronę, a zwroty przeciwne wskazują w różne kierunki.
- W analizie wektorów zwrot ma kluczowe znaczenie dla operacji takich jak dodawanie i odejmowanie wektorów.
- Wektory różnią się od siebie nie tylko kierunkiem, ale także długością i punktem zaczepienia.
- Wizualizacja zwrotu wektora jest istotna dla lepszego zrozumienia jego właściwości i zastosowań.
Definicja zwrotu w fizyce i jego znaczenie dla wektorów
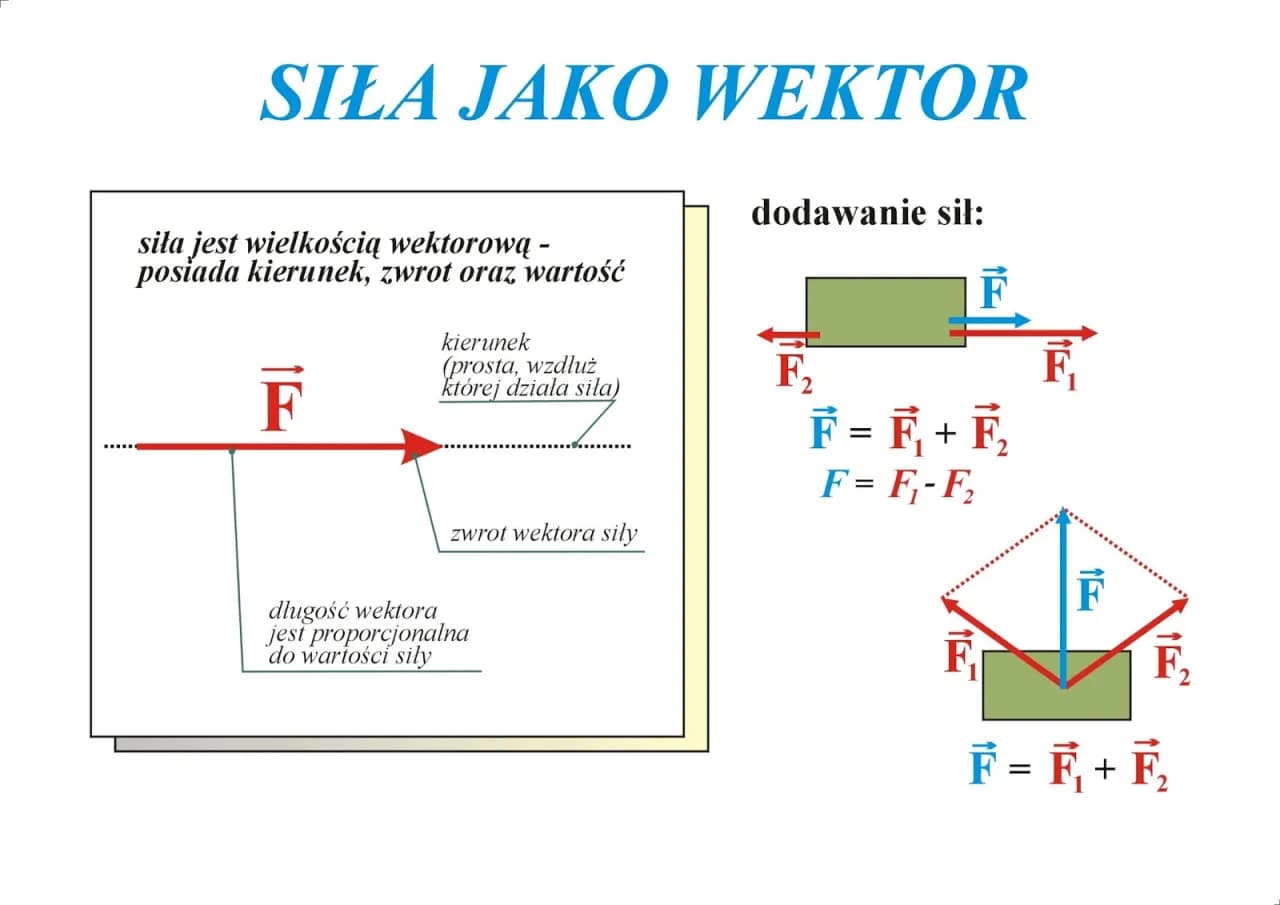
Zwrot wektora w fizyce to fundamentalna cecha, która definiuje kierunek, w jakim wskazuje dany wektor. Jest to niezwykle istotne dla zrozumienia zjawisk fizycznych, ponieważ zwrot determinuje, jak różne wektory współdziałają ze sobą. Wektory są używane do opisu wielu zjawisk, takich jak siły, prędkości czy przyspieszenia, dlatego zrozumienie ich zwrotu jest kluczowe dla studentów fizyki oraz inżynierów.
W praktyce, zwrot wektora można zobrazować jako kierunek, w którym strzałka wektora jest skierowana. Dwa wektory mają ten sam zwrot, jeśli są skierowane w tę samą stronę. Z kolei, jeśli są skierowane w przeciwnych kierunkach, mówimy, że mają zwroty przeciwne. Ta właściwość jest niezbędna do analizy i rozwiązywania problemów związanych z wektorami.
Co to jest zwrot wektora i jak go zrozumieć?
Zwrot wektora można zdefiniować jako kierunek, w którym strzałka wektora wskazuje w przestrzeni. Jest to kluczowy aspekt, który różni wektory od skalarów, które mają tylko wartość, ale nie kierunek. W fizyce, zwrot jest reprezentowany na płaszczyźnie lub w przestrzeni trójwymiarowej, co pozwala na dokładne modelowanie ruchu obiektów oraz interakcji między nimi.
Jak zwrot wpływa na analizę wektorów w fizyce?
Zwrot wektora ma kluczowe znaczenie w analizie wektorów, ponieważ wpływa na sposób, w jaki wektory są dodawane i odejmowane. Gdy dodajemy dwa wektory, ich zwroty muszą być uwzględnione, aby uzyskać poprawny wynik. Na przykład, jeśli dwa wektory mają ten sam zwrot, ich wartości będą się sumować, co prowadzi do powstania nowego wektora o większej długości. Z kolei, jeśli wektory mają przeciwny zwrot, ich wartości będą się odejmować, co może prowadzić do zmniejszenia długości rezultatu lub nawet do uzyskania wektora o zerowej długości.
W przypadku odejmowania wektorów, zwrot również odgrywa istotną rolę. Odejmowanie wektora A od wektora B można zinterpretować jako dodawanie wektora B do wektora A o przeciwnym zwrocie. To pokazuje, że zrozumienie zwrotu wektora jest niezbędne do prawidłowego przeprowadzania operacji wektorowych. W analizie wektorów, zwrot jest zatem kluczowym czynnikiem, który wpływa na wyniki obliczeń oraz interpretację zjawisk fizycznych.
Właściwości wektorów związane ze zwrotem
Wektory charakteryzują się różnymi właściwościami związanymi z ich zwrotem. Jedną z najważniejszych różnic jest to, że zwrot wektora jest niezależny od jego długości. Oznacza to, że dwa wektory mogą mieć tę samą długość, ale różne zwroty, a tym samym różne znaczenie fizyczne. W praktyce, wektory o przeciwnych zwrotach będą działać w przeciwnych kierunkach, co jest kluczowe w analizie sił i ruchu.
Inną istotną właściwością jest to, że zwrot wektora może być zmieniany, co jest wykorzystywane w różnych zastosowaniach inżynieryjnych i fizycznych. Na przykład, w mechanice, zmiana zwrotu siły może prowadzić do zmiany kierunku ruchu obiektu. W związku z tym, zrozumienie zwrotu wektora jest kluczowe dla efektywnego modelowania i analizy zjawisk fizycznych, a także dla rozwiązywania problemów inżynieryjnych.
Jakie są różnice między zwrotem a kierunkiem wektora?
Zwrot i kierunek wektora to dwa różne, ale powiązane pojęcia w fizyce. Zwrot odnosi się do tego, w którą stronę wskazuje wektor, co jest kluczowe dla zrozumienia interakcji między różnymi wektorami. Z kolei kierunek dotyczy orientacji wektora w przestrzeni, która może być reprezentowana w różnych układach odniesienia. W praktyce, kierunek może być opisany jako kąt, pod jakim wektor jest skierowany w stosunku do osi współrzędnych.
Warto zauważyć, że dwa wektory mogą mieć ten sam kierunek, ale różne zwroty. Na przykład, wektor A może wskazywać w górę, a wektor B może wskazywać w dół, mimo że oba mają ten sam kierunek, jeśli mówimy o osi pionowej. Zrozumienie tej różnicy jest kluczowe, ponieważ wpływa na sposób, w jaki analizujemy i interpretujemy siły oraz ruchy w fizyce.
Jakie są przykłady wektorów o tym samym i przeciwnym zwrocie?
Przykłady wektorów o tym samym i przeciwnym zwrocie można znaleźć w wielu zjawiskach fizycznych. Na przykład, jeśli mamy dwa wektory siły: jeden o wartości 5 N skierowany w prawo i drugi o wartości 5 N również skierowany w prawo, to oba mają ten sam zwrot. W takim przypadku, gdy są dodawane, ich suma wynosi 10 N w prawo, co ilustruje, jak wektory o tym samym zwrocie współdziałają ze sobą.
- Wektor siły 5 N w prawo i 5 N w prawo – ten sam zwrot, suma 10 N w prawo.
- Wektor siły 5 N w prawo i 5 N w lewo – przeciwny zwrot, suma 0 N.
- Wektor prędkości 10 m/s w górę i 10 m/s w górę – ten sam zwrot, suma 20 m/s w górę.
Czytaj więcej: Terminy powrotu szkół po feriach - kalendarz i najnowsze informacje
Wizualizacja zwrotu wektora w przestrzeni

Wizualizacja zwrotu wektora jest kluczowym elementem w analizie wektorów, ponieważ pozwala zrozumieć, jak wektory oddziałują ze sobą w przestrzeni. Istnieje wiele metod, które można wykorzystać do przedstawienia zwrotu wektora, w tym diagramy, grafiki komputerowe oraz modele 3D. Dzięki tym technikom, można zobaczyć, jak różne wektory są skierowane względem siebie, co jest niezbędne w fizyce, aby zrozumieć dynamikę ruchu i interakcje sił.
Jednym z najpopularniejszych sposobów wizualizacji wektorów jest użycie diagramów strzałkowych, które przedstawiają wektory jako strzałki o określonej długości i kierunku. Długość strzałki reprezentuje wartość wektora, a kierunek pokazuje jego zwrot. W przypadku bardziej złożonych analiz, narzędzia komputerowe mogą generować interaktywne wizualizacje, które pozwalają na manipulację wektorami w czasie rzeczywistym, co ułatwia zrozumienie ich zachowania w różnych sytuacjach.
Jak używać grafiki do przedstawienia zwrotu wektora?
Grafika jest niezwykle pomocna w przedstawianiu zwrotu wektora, ponieważ umożliwia wizualizację złożonych koncepcji w prosty sposób. Używając programów graficznych, takich jak GeoGebra czy MATLAB, można tworzyć dynamiczne wykresy, które ilustrują zmiany zwrotu wektora w czasie. Takie narzędzia pozwalają na łatwe manipulowanie danymi i obserwowanie, jak zmiany w zwrocie wpływają na wynikowe wektory.
- Diagramy strzałkowe ilustrujące kierunek i wartość wektora.
- Interaktywne wizualizacje umożliwiające manipulację wektorami w czasie rzeczywistym.
- Wykresy generowane w programach takich jak GeoGebra, które pokazują zmiany zwrotu wektora.
Jakie narzędzia można wykorzystać do analizy zwrotu wektora?
W analizie zwrotu wektora w fizyce istnieje wiele narzędzi i oprogramowania, które mogą znacząco ułatwić zrozumienie i wizualizację tego pojęcia. Programy takie jak GeoGebra i MATLAB oferują zaawansowane funkcje graficzne, które pozwalają na tworzenie interaktywnych wykresów i modeli wektorowych. Dzięki nim można łatwo manipulować wektorami i obserwować, jak zmiany w zwrocie wpływają na wyniki obliczeń.
Inne przydatne narzędzia to Python z bibliotekami takimi jak Matplotlib oraz NumPy, które umożliwiają programistyczną analizę wektorów i ich wizualizację. Te narzędzia są szczególnie cenione w środowisku akademickim oraz w przemyśle, gdzie precyzyjna analiza danych jest kluczowa. Wybierając narzędzia do analizy zwrotu wektora, warto zwrócić uwagę na ich funkcjonalność, łatwość użycia oraz możliwość integracji z innymi systemami.Nowe trendy w analizie wektorów: sztuczna inteligencja i uczenie maszynowe
W miarę jak technologia rozwija się, sztuczna inteligencja (AI) i uczenie maszynowe zaczynają odgrywać coraz większą rolę w analizie wektorów i ich wizualizacji. Te zaawansowane techniki mogą być wykorzystane do automatyzacji procesów analitycznych, co pozwala na szybsze i dokładniejsze obliczenia. Na przykład, algorytmy uczenia maszynowego mogą pomóc w przewidywaniu zachowań systemów fizycznych na podstawie analizy dużych zbiorów danych dotyczących wektorów, co ma zastosowanie w takich dziedzinach jak inżynieria, meteorologia czy robotyka.Co więcej, integracja technologii VR (wirtualnej rzeczywistości) z analizą wektorów otwiera nowe możliwości wizualizacji. Użytkownicy mogą zanurzyć się w interaktywnych środowiskach, gdzie mogą manipulować wektorami w trójwymiarowej przestrzeni, co znacznie ułatwia zrozumienie złożonych koncepcji fizycznych. Takie podejście nie tylko zwiększa zaangażowanie uczniów, ale także pozwala na bardziej intuicyjne przyswajanie wiedzy o zwrocie wektora i jego zastosowaniach w rzeczywistych scenariuszach.