Równanie sprzeczne to pojęcie, które odnosi się do równań matematycznych, które nie mają żadnego rozwiązania. W praktyce oznacza to, że po przekształceniu takiego równania otrzymujemy zawsze nieprawdziwą równość, na przykład $7=11$ lub $x^2=-9$. Takie równania mogą wydawać się trudne do zrozumienia, ale ich analiza jest kluczowa w matematyce, ponieważ pomagają zrozumieć, kiedy pewne wyrażenia nie mają sensu w kontekście liczbowym.
W tym artykule przyjrzymy się bliżej temu, czym jest równanie sprzeczne, jakie są jego cechy oraz jak można je rozpoznać. Dzięki temu zyskasz lepsze zrozumienie tego zagadnienia i nauczysz się, jak unikać błędów podczas rozwiązywania równań w przyszłości.Kluczowe informacje:
- Równanie sprzeczne nie ma rozwiązania, co oznacza, że nie istnieje żadna wartość, która spełniałaby to równanie.
- Przykłady równań sprzecznych to $7=11$ oraz $x^2=-9$.
- Równania sprzeczne mogą pojawiać się w różnych kontekstach matematycznych, a ich identyfikacja jest kluczowa dla poprawnego rozwiązywania problemów.
- W analizie równań sprzecznych ważne jest zrozumienie ich właściwości, co pomaga uniknąć błędów w obliczeniach.
Definicja równania sprzecznego i jego podstawowe cechy
Równanie sprzeczne to termin, który odnosi się do równań matematycznych, które nie mają żadnego rozwiązania. Oznacza to, że po przekształceniu takiego równania zawsze otrzymujemy nieprawdziwą równość, na przykład $7=11$ lub $x^2=-9$. Zrozumienie tego pojęcia jest kluczowe w matematyce, ponieważ pozwala na identyfikację sytuacji, w których pewne równości nie mają sensu.
W matematyce, definicja równania sprzecznego jest istotna, ponieważ pomaga w rozwiązywaniu problemów oraz w analizie złożonych sytuacji. Wiedza o tym, jak rozpoznać takie równania, jest niezbędna dla każdego, kto zajmuje się matematyką, niezależnie od poziomu zaawansowania. Równania sprzeczne mogą pojawiać się w różnych kontekstach, a ich zrozumienie może znacząco wpłynąć na prawidłowość obliczeń.
Jak zdefiniować równanie sprzeczne w matematyce?
Formalnie, równanie sprzeczne to takie, które nie ma rozwiązania, co oznacza, że nie istnieje żadna wartość zmiennej, która mogłaby je spełnić. W matematyce, gdy analizujemy równania, napotykamy na sytuacje, w których po przekształceniach dochodzimy do sprzeczności. Przykładowo, jeśli przekształcimy równanie do postaci, w której obie strony są sobie równe, ale prowadzą do fałszywego stwierdzenia, mamy do czynienia z równaniem sprzecznym.
Warto zauważyć, że definicja równania sprzecznego jest kluczowa dla zrozumienia podstawowych zasad matematyki. Pomaga to uczniom i studentom w nauce oraz w zrozumieniu, dlaczego pewne równania nie mają sensu. Dzięki tej wiedzy można unikać błędów w obliczeniach i lepiej zrozumieć złożoność równań matematycznych.
Jakie są kluczowe cechy równania sprzecznego?
Równania sprzeczne charakteryzują się kilkoma kluczowymi cechami, które pozwalają na ich identyfikację. Przede wszystkim, brak rozwiązania jest ich najważniejszą właściwością. Oznacza to, że nie istnieje żadna wartość zmiennej, która mogłaby spełnić dane równanie. Często po przekształceniach dochodzi do sytuacji, w której obie strony równania prowadzą do sprzeczności, co skutkuje nieprawdziwą równością.
Inną istotną cechą jest niespójność wynikająca z takich równań. Równania sprzeczne mogą występować w różnych kontekstach matematycznych, a ich analiza jest kluczowa dla zrozumienia złożoności problemów. W praktyce, identyfikacja tych równań jest niezbędna do unikania błędów w obliczeniach oraz w zrozumieniu, dlaczego pewne wyrażenia nie mają sensu.
Przykłady równania sprzecznego w praktyce
Równania sprzeczne można spotkać w różnych dziedzinach matematyki. Proste przykłady, takie jak $7=11$, pokazują, że nie ma możliwości, aby obie strony były równe. Innym przykładem jest równanie $x^2=-9$, które również nie ma rozwiązania w zbiorze liczb rzeczywistych. Takie przypadki są łatwe do zidentyfikowania i pomagają w nauce.
| Równanie | Opis |
| $7=11$ | Prosta sprzeczność, która nie ma rozwiązania. |
| $x^2=-9$ | Brak rozwiązania w zbiorze liczb rzeczywistych. |
| $2x + 3 = 2x + 5$ | Po uproszczeniu prowadzi do sprzeczności $3=5$. |
Przykłady prostych równań sprzecznych i ich rozwiązania
Proste równania sprzeczne są doskonałym przykładem tego, jak niektóre wyrażenia matematyczne mogą prowadzić do sprzeczności. Na przykład, równanie $3 + 2 = 10$ jest sprzeczne, ponieważ po dodaniu 3 i 2 otrzymujemy 5, a nie 10. Innym przykładem jest równanie $x - 4 = x + 2$. Po przekształceniach dochodzimy do $-4 = 2$, co również jest oczywistą nieprawdą. Takie równania pokazują, że nie ma możliwości, aby istniała wartość zmiennej, która spełniałaby te równania.
Warto zauważyć, że proste równania sprzeczne są istotne dla nauki matematyki, ponieważ pomagają w zrozumieniu, jak ważne jest poprawne przekształcanie równań. Dzięki nim uczniowie mogą nauczyć się, jak unikać błędów w obliczeniach i lepiej rozumieć zasady działania równań. Przykłady te pokazują, że nie każde równanie ma rozwiązanie, co jest kluczowe w matematyce.
Analiza bardziej złożonych równań sprzecznych
W przypadku bardziej złożonych równań sprzecznych, analiza staje się nieco bardziej skomplikowana. Na przykład, rozważmy równanie $2(x - 3) = 2x - 6$. Po przekształceniach, możemy zauważyć, że obie strony równania są sobie równe, co może wprowadzać w błąd. Jednak, jeśli dodamy dodatkowy warunek, taki jak $0 = 5$, otrzymujemy sprzeczność. Takie sytuacje pokazują, jak ważne jest dokładne przekształcanie równań oraz zrozumienie, że niektóre równania mogą wydawać się prawdziwe, ale w rzeczywistości prowadzą do sprzeczności.
Analiza złożonych równań sprzecznych ma kluczowe znaczenie w matematyce, ponieważ pozwala na lepsze zrozumienie struktury równań oraz ich właściwości. Umożliwia to także studentom rozwijanie umiejętności krytycznego myślenia i logicznego rozumowania, które są niezbędne w rozwiązywaniu bardziej skomplikowanych problemów matematycznych.
Jak identyfikować równania sprzeczne w zadaniach matematycznych?
Identyfikacja równań sprzecznych w zadaniach matematycznych jest kluczowa dla poprawnego rozwiązywania problemów. Istnieje kilka technik, które mogą pomóc w wykrywaniu takich równań. Po pierwsze, warto zwrócić uwagę na wyniki przekształceń, które prowadzą do nieprawdziwych równości, takich jak $7=11$. Po drugie, analiza postaci równań i ich rozwiązań może ujawnić sprzeczności, zwłaszcza gdy pojawiają się sprzeczne wartości zmiennej. Kluczowe jest również sprawdzanie, czy po podstawieniu wartości do równania otrzymujemy prawdziwe stwierdzenia.
- Sprawdzanie, czy przekształcone równanie prowadzi do fałszywej równości.
- Analiza postaci równań i ich rozwiązań pod kątem sprzecznych wartości.
- Podstawianie wartości do równań, aby zweryfikować ich prawdziwość.
Metody wykrywania sprzeczności w równaniach
Wykrywanie sprzeczności w równaniach można przeprowadzać za pomocą różnych metod. Jedną z najczęściej stosowanych jest metoda podstawiania, która polega na wstawieniu wartości zmiennych do równania. Jeśli po podstawieniu otrzymamy sprzeczność, oznacza to, że równanie jest sprzeczne. Inną metodą jest metoda eliminacji, w której z równań odejmujemy lub dodajemy równania, aby uprościć problem. Jeśli po eliminacji zmiennych dojdziemy do sprzeczności, również potwierdza to, że równanie jest sprzeczne.
Obie te metody są skuteczne i pozwalają na szybkie zidentyfikowanie równań sprzecznych. Warto je stosować w praktyce, aby unikać błędów w obliczeniach i lepiej zrozumieć struktury równań matematycznych.
Wskazówki do rozwiązywania równań sprzecznych
Rozwiązywanie równań sprzecznych wymaga szczególnej uwagi i podejścia. Po pierwsze, zawsze warto dokładnie sprawdzić, czy równanie zostało poprawnie przekształcone. Używaj różnych metod, takich jak podstawianie i eliminacja, aby upewnić się, że nie przegapiłeś żadnej sprzeczności. Ponadto, analizuj wyniki przekształceń, które prowadzą do nieprawdziwych równości, co może wskazywać na sprzeczność. Ostatecznie, jeśli napotkasz równanie, które wydaje się nie mieć rozwiązania, potwierdź to, próbując podstawić różne wartości zmiennych i sprawdzając, czy równanie pozostaje prawdziwe.
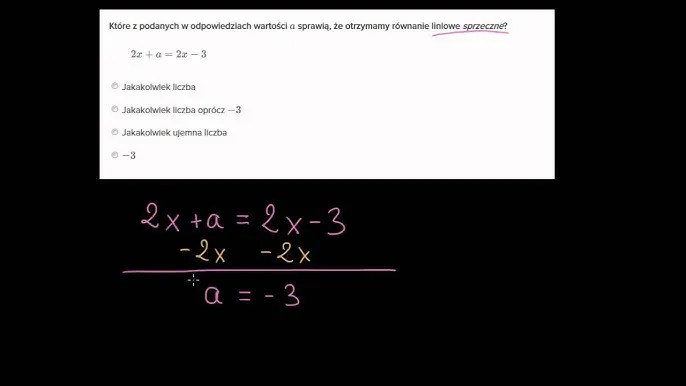
Znaczenie równań sprzecznych w kontekście matematyki
Równania sprzeczne mają istotne znaczenie w teorii matematycznej i praktycznych zastosowaniach. Pomagają one w zrozumieniu granic możliwości równań oraz w identyfikacji sytuacji, w których pewne założenia prowadzą do błędnych wniosków. Analizowanie równań sprzecznych uczy matematyki krytycznego myślenia i logicznego rozumowania, co jest niezbędne w bardziej zaawansowanych dziedzinach. W praktyce, znajomość tych równań pozwala na unikanie błędów i lepsze rozwiązywanie problemów matematycznych.
Jak wykorzystać równania sprzeczne w rozwoju umiejętności matematycznych
Równania sprzeczne mogą być nie tylko przeszkodą w rozwiązywaniu problemów, ale także cennym narzędziem w rozwijaniu umiejętności matematycznych. Używanie ich w ćwiczeniach pozwala na lepsze zrozumienie logiki matematycznej oraz umiejętności krytycznego myślenia. Uczniowie mogą ćwiczyć identyfikację sprzeczności w równaniach, co pozwala im na rozwijanie zdolności analitycznych, które są niezbędne w bardziej zaawansowanych tematach, takich jak algebra czy analiza matematyczna.
Co więcej, w kontekście nowoczesnych technologii edukacyjnych, aplikacje i programy komputerowe mogą symulować różne scenariusze równań sprzecznych, oferując interaktywne doświadczenia w nauce. Dzięki takim narzędziom, uczniowie mogą na bieżąco obserwować efekty swoich przekształceń i lepiej zrozumieć, jak unikać błędów w obliczeniach. W przyszłości, integracja sztucznej inteligencji w edukacji matematycznej może dodatkowo wspierać proces nauczania, oferując spersonalizowane ćwiczenia dostosowane do indywidualnych potrzeb ucznia.
