Wyrazy sumy algebraicznej to kluczowy element w matematyce, który odgrywa istotną rolę w rozwiązywaniu równań i analizie wyrażeń algebraicznych. W prostych słowach, wyrazami sumy algebraicznej są pojedyncze jednomiany, które są dodawane lub odejmowane w danym wyrażeniu. Zrozumienie, czym są te wyrazy i jak je identyfikować, jest niezbędne do skutecznego posługiwania się algebrą.
W naszym artykule przyjrzymy się definicji wyrazów sumy algebraicznej oraz ich znaczeniu w kontekście obliczeń matematycznych. Omówimy także, jak znaki przed wyrazami wpływają na wyniki oraz jakie praktyczne zastosowania mają te wyrazy w rozwiązywaniu równań. Dzięki temu łatwiej będzie zrozumieć, jak działa algebra i jak można wykorzystać te informacje w praktyce.
Kluczowe informacje:
- Wyrazy sumy algebraicznej to pojedyncze jednomiany, które są dodawane lub odejmowane.
- Suma algebraiczna składa się z tych jednomianów, które są brane pod uwagę z odpowiednimi znakami.
- Identyfikacja wyrazów w wyrażeniach algebraicznych jest kluczowa dla poprawnych obliczeń.
- Znaki przed wyrazami mają znaczący wpływ na wyniki sumy algebraicznej.
- Wyrazy sumy algebraicznej pomagają w rozwiązywaniu równań i innych problemów matematycznych.
Co to są wyrazy sumy algebraicznej i ich podstawowe znaczenie
Wyrazy sumy algebraicznej to pojedyncze jednomiany, które są dodawane lub odejmowane w danym wyrażeniu. Każdy z tych jednomianów stanowi wyraz tej sumy, co oznacza, że suma algebraiczna jest zbiorem tych wyrazów. Zrozumienie, czym są wyrazy sumy algebraicznej, jest kluczowe dla skutecznego posługiwania się algebrą. Warto pamiętać, że wyrazy sumy bierzemy pod uwagę z odpowiednimi znakami, które je poprzedzają, co wpływa na wynik całej sumy. Na przykład w wyrażeniu algebraicznym, takim jak $$3x^2 + 2x - 5 - 3x + 1$$, wyrazami tej sumy są: $$3x^2$$, $$2x$$, $$-5$$, $$-3x$$ oraz $$1$$.
Definicja wyrazów w sumie algebraicznej i ich rola
Definiując wyrazy w sumie algebraicznej, można stwierdzić, że są to elementy składające się na wyrażenie algebraiczne, które mogą być zarówno dodatnie, jak i ujemne. Każdy wyraz jest oddzielony znakiem + lub - i tworzy razem z innymi wyrazami całość, która jest sumą algebraiczną. Rola wyrazów polega na tym, że umożliwiają one operacje matematyczne, takie jak dodawanie i odejmowanie, które są fundamentalne w rozwiązywaniu równań i analizie algebraicznej. Zrozumienie tej definicji jest niezbędne, aby móc poprawnie pracować z wyrażeniami algebraicznymi.
Jak identyfikować wyrazy w różnych wyrażeniach algebraicznych
Identyfikacja wyrazów w wyrażeniach algebraicznych jest kluczowa dla zrozumienia, jak działają te wyrażenia. Wyrazy sumy algebraicznej można łatwo zidentyfikować, zwracając uwagę na znaki + i -, które oddzielają poszczególne jednomiany. Każdy wyraz jest oddzielnym elementem i może mieć różne współczynniki oraz zmienne. Dobrym sposobem na identyfikację wyrazów jest przekształcenie wyrażenia w bardziej czytelną formę, na przykład poprzez uporządkowanie ich według zmiennych lub ich wartości. Warto również zwracać uwagę na nawiasy, które mogą wpływać na to, jak wyrazy są grupowane w danym wyrażeniu.
Jak wyrazy sumy algebraicznej wpływają na obliczenia
Wyrazy sumy algebraicznej mają znaczący wpływ na obliczenia matematyczne. Każdy wyraz, będący jednomianem, przyczynia się do ostatecznego wyniku sumy algebraicznej. W przypadku dodawania lub odejmowania wyrazów, ich wartości oraz znaki decydują o tym, czy wynik będzie dodatni, czy ujemny. Zrozumienie, jak poszczególne wyrazy wpływają na obliczenia, pozwala na dokładniejsze wykonywanie działań matematycznych oraz rozwiązywanie równań. Dlatego tak ważne jest, aby umieć poprawnie identyfikować i analizować wyrazy w różnych wyrażeniach algebraicznych.
Znaczenie znaków przed wyrazami w sumie algebraicznej
Znaki przed wyrazami w sumie algebraicznej mają kluczowe znaczenie dla ostatecznego wyniku wyrażenia. Znaki + i - określają, czy dany wyraz będzie dodawany do sumy, czy odejmowany. Na przykład, w wyrażeniu $$3x^2 + 2x - 5$$, wyraz $$-5$$ jest odejmowany, co wpływa na całkowity wynik sumy. Ignorowanie znaków może prowadzić do błędnych obliczeń, dlatego ich poprawna interpretacja jest niezbędna w każdym działaniu matematycznym. Zrozumienie roli znaków pozwala na skuteczniejsze rozwiązywanie równań i analizę wyrażeń algebraicznych.
Przykłady wpływu wyrazów na wynik sumy algebraicznej
Różne wyrazy w sumie algebraicznej mogą znacząco wpłynąć na ostateczny wynik. Na przykład, w wyrażeniu $$4x + 3 - 2x + 5$$, wyrazy $$4x$$ i $$-2x$$ mają różne znaki, co prowadzi do uproszczenia do $$2x + 8$$. W innym przypadku, w wyrażeniu $$-7 + 3x - 2$$, suma wyrazów $$-7$$ i $$-2$$ daje $$-9$$, co znacznie obniża wartość całego wyrażenia. Takie przykłady pokazują, jak istotne jest zrozumienie, jak poszczególne wyrazy i ich znaki wpływają na wynik sumy algebraicznej.
| Wyrażenie algebraiczne | Wynik uproszczony |
| 4x + 3 - 2x + 5 | 2x + 8 |
| -7 + 3x - 2 | 3x - 9 |
| 3x^2 - 4 + 2x + 1 | 3x^2 + 2x - 3 |
Czytaj więcej: Co to wyrażenia algebraiczne? Zrozumienie ich znaczenia i zastosowania
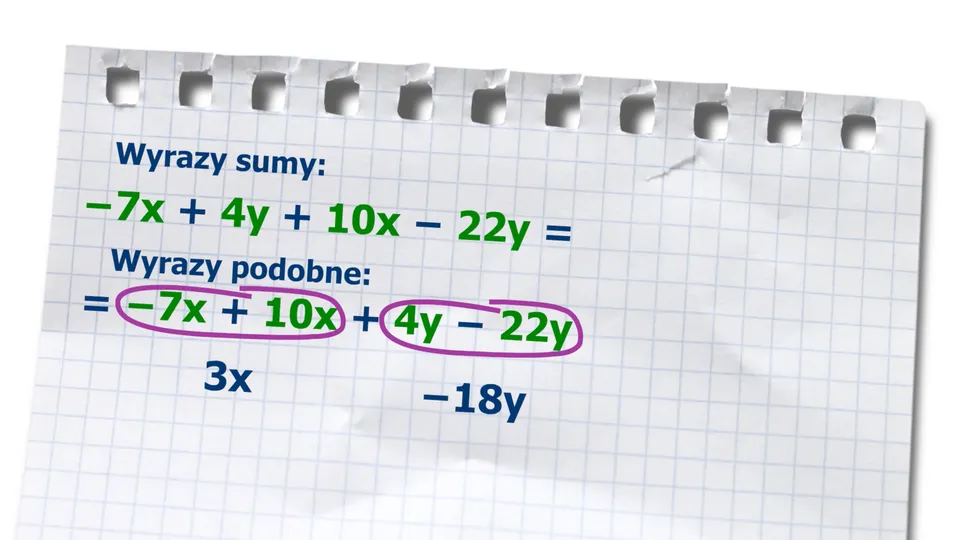
Praktyczne zastosowania wyrazów sumy algebraicznej w matematyce
Wyrazy sumy algebraicznej mają wiele praktycznych zastosowań w matematyce, zwłaszcza w kontekście rozwiązywania równań i analizy funkcji. Dzięki umiejętności identyfikacji i manipulacji wyrazami, możemy skutecznie rozwiązywać złożone problemy matematyczne. Na przykład, w obliczeniach związanych z funkcjami kwadratowymi, wyrazy te pozwalają na przekształcanie równań, co ułatwia znajdowanie miejsc zerowych funkcji. Umiejętność pracy z wyrazami jest również niezbędna w zastosowaniach inżynieryjnych, gdzie algebra jest często wykorzystywana do modelowania różnych zjawisk. Wreszcie, wyrazy sumy algebraicznej są kluczowe w statystyce, gdzie pomagają w analizie danych i obliczeniach statystycznych.
Jak wyrazy sumy algebraicznej pomagają w rozwiązywaniu równań
Wyrazy sumy algebraicznej odgrywają fundamentalną rolę w rozwiązywaniu równań. Każdy wyraz, będący jednomianem, przyczynia się do formułowania równań, które można rozwiązać za pomocą różnych metod. Na przykład, w równaniach liniowych, takie jak $$2x + 3 = 7$$, wyrazy są kluczowe do przekształcenia równania w postać, która umożliwia łatwe obliczenie wartości zmiennej. W przypadku równań kwadratowych, wyrazy pozwalają na użycie wzorów kwadratowych do znalezienia miejsc zerowych funkcji. W ten sposób, wyrazy sumy algebraicznej nie tylko ułatwiają rozwiązywanie równań, ale także zwiększają naszą zdolność do analizy i interpretacji wyników.
- Nie ignoruj znaków: Zawsze zwracaj uwagę na znaki + i -, ponieważ mają kluczowe znaczenie dla wyniku końcowego.
- Uważaj na nawiasy: Upewnij się, że prawidłowo stosujesz nawiasy, aby uniknąć błędnych interpretacji wyrazów.
- Sprawdzaj obliczenia: Po wykonaniu obliczeń, zweryfikuj wyniki, aby upewnić się, że nie popełniłeś błędów w dodawaniu lub odejmowaniu wyrazów.
- Praktykuj regularnie: Im więcej ćwiczysz, tym lepiej zrozumiesz, jak wyrazy sumy algebraicznej wpływają na obliczenia.
- Analizuj przykłady: Używaj konkretnych przykładów, aby lepiej zrozumieć, jak poszczególne wyrazy oddziałują na siebie w różnych wyrażeniach.
Jak wykorzystać wyrazy sumy algebraicznej w programowaniu matematycznym
W dzisiejszych czasach umiejętność pracy z wyrazami sumy algebraicznej nie ogranicza się tylko do tradycyjnej matematyki. Programowanie matematyczne staje się coraz bardziej popularne, a znajomość wyrazów algebraicznych może znacząco ułatwić tworzenie algorytmów i rozwiązywanie problemów. Na przykład, w językach programowania takich jak Python, można wykorzystać biblioteki matematyczne do automatyzacji obliczeń związanych z wyrazami algebraicznymi. Dzięki temu, skomplikowane operacje, takie jak faktoryzacja czy uproszczenie wyrażeń, stają się znacznie prostsze i szybsze.
Co więcej, w kontekście analizy danych, umiejętność manipulowania wyrazami sumy algebraicznej pozwala na lepsze modelowanie zjawisk i przewidywanie wyników. Na przykład, w analizie regresji, wyrazy algebraiczne są używane do tworzenia modeli, które pomagają w prognozowaniu trendów. W miarę jak technologia rozwija się, umiejętność łączenia matematyki z programowaniem stanie się kluczowa w wielu dziedzinach, takich jak inżynieria, finanse czy nauki przyrodnicze.
