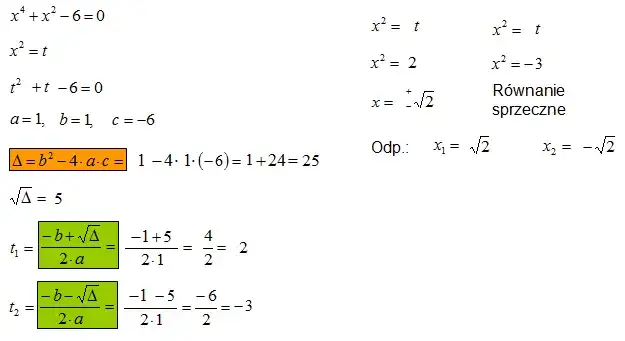Rozwiązywanie równań kwadratowych to kluczowa umiejętność w matematyce, która ma zastosowanie w wielu dziedzinach, od nauk ścisłych po inżynierię. Równania kwadratowe mają postać $$ax^2 + bx + c = 0$$, gdzie $$a$$, $$b$$ i $$c$$ to współczynniki. Aby znaleźć rozwiązania, najpierw oblicza się wartość delty (Δ) za pomocą wzoru $$\Delta = b^2 - 4ac$$. W zależności od wartości delty można określić, ile rozwiązań rzeczywistych ma dane równanie.
W tym artykule przedstawimy proste metody rozwiązywania równań kwadratowych oraz podamy konkretne przykłady. Omówimy różne przypadki wartości delty i pokażemy, jak obliczać pierwiastki równania, a także zaprezentujemy alternatywne metody, takie jak faktoryzacja. Dzięki temu każdy, kto chce nauczyć się rozwiązywania równań kwadratowych, znajdzie przydatne informacje i praktyczne wskazówki.
Najistotniejsze informacje:
- Równania kwadratowe mają postać $$ax^2 + bx + c = 0$$.
- Delta (Δ) oblicza się ze wzoru $$\Delta = b^2 - 4ac$$.
- Wartości delty decydują o liczbie rozwiązań równania: $$\Delta > 0$$ - dwa pierwiastki, $$\Delta = 0$$ - jeden pierwiastek, $$\Delta < 0$$ - brak rozwiązań rzeczywistych.
- Można rozwiązywać równania kwadratowe poprzez faktoryzację, wzór kwadratowy lub inne metody.
- Przykłady ilustrujące różne metody pomogą w zrozumieniu procesu rozwiązywania równań.
Zrozumienie równań kwadratowych i ich znaczenie w matematyce
Równania kwadratowe to szczególny typ równań, które mają postać $$ax^2 + bx + c = 0$$, gdzie $$a$$, $$b$$ i $$c$$ to stałe liczby, a $$x$$ to zmienna. W tej formie $$a$$ nie może być równe zero, ponieważ w przeciwnym razie równanie przestaje być kwadratowe. Równania te są niezwykle ważne w matematyce, ponieważ pojawiają się w wielu zastosowaniach, od fizyki po ekonomię, a także w różnych dziedzinach inżynierii.
Warto zauważyć, że rozwiązywanie równań kwadratowych pozwala na znalezienie wartości zmiennej $$x$$, które sprawiają, że równanie jest spełnione. Dzięki temu możemy modelować różne zjawiska i problemy praktyczne. Na przykład, w fizyce równania kwadratowe mogą pomóc w obliczeniach związanych z ruchem ciał, a w ekonomii mogą służyć do analizy kosztów i przychodów. Zrozumienie tego typu równań jest kluczowe dla dalszego rozwoju umiejętności matematycznych i analitycznych.
Jak się rozwiązuje równania kwadratowe - krok po kroku
Rozwiązywanie równań kwadratowych wymaga zastosowania kilku kroków, które prowadzą do znalezienia pierwiastków równania. Pierwszym krokiem jest przekształcenie równania do postaci ogólnej $$ax^2 + bx + c = 0$$, jeśli nie jest już w tej formie. Następnie, należy obliczyć wartość delty (Δ) za pomocą wzoru $$\Delta = b^2 - 4ac$$. Delta jest kluczowa, ponieważ jej wartość determinuje liczbę i rodzaj rozwiązań, jakie równanie może mieć.
Ważne jest, aby dokładnie śledzić poszczególne kroki, ponieważ każdy z nich wpływa na ostateczny wynik. Po obliczeniu delty, w zależności od jej wartości, możemy zastosować odpowiednie wzory do obliczenia pierwiastków. Przykładowo, jeśli $$\Delta > 0$$, równanie ma dwa różne pierwiastki rzeczywiste, natomiast jeśli $$\Delta = 0$$, istnieje jeden podwójny pierwiastek. Uważne podejście do każdego z tych kroków zapewnia prawidłowe rozwiązanie równań kwadratowych.Wyznaczanie delty (Δ) i jej znaczenie w rozwiązaniach
Aby zrozumieć, jak się rozwiązuje równania kwadratowe, kluczowym krokiem jest obliczenie wartości delty (Δ). Delta jest obliczana za pomocą wzoru $$\Delta = b^2 - 4ac$$, gdzie $$a$$, $$b$$ i $$c$$ to współczynniki równania kwadratowego w postaci $$ax^2 + bx + c = 0$$. Wartość delty ma ogromne znaczenie, ponieważ decyduje o liczbie i rodzaju rozwiązań równania. Gdy $$\Delta > 0$$, równanie ma dwa różne pierwiastki rzeczywiste, co oznacza, że funkcja kwadratowa przecina oś x w dwóch punktach. Z kolei, gdy $$\Delta = 0$$, istnieje jeden pierwiastek podwójny, co wskazuje, że funkcja dotyka osi x w jednym punkcie.
Natomiast, gdy $$\Delta < 0$$, równanie nie ma rozwiązań rzeczywistych, co oznacza, że pierwiastki są zespolone. To zrozumienie delty jest kluczowe dla dalszego procesu rozwiązywania równań kwadratowych, ponieważ pozwala na przewidzenie, jakie rodzaje rozwiązań można oczekiwać. Dlatego obliczenie delty jest niezbędnym krokiem, który umożliwia dalsze działania związane z wyznaczaniem pierwiastków równania.
Obliczanie pierwiastków równania kwadratowego - metody
Po obliczeniu delty, kolejnym krokiem w procesie rozwiązywania równań kwadratowych jest wyznaczenie pierwiastków równania. W zależności od wartości delty, stosuje się różne metody. Jeśli $$\Delta > 0$$, pierwiastki oblicza się za pomocą wzorów: $$x_1 = \frac{-b - \sqrt{\Delta}}{2a}$$ oraz $$x_2 = \frac{-b + \sqrt{\Delta}}{2a}$$. Te wzory pozwalają na uzyskanie dwóch różnych rozwiązań rzeczywistych. W przypadku, gdy $$\Delta = 0$$, stosuje się prostszy wzór $$x = -\frac{b}{2a}$$, który daje jeden pierwiastek podwójny.
W sytuacji, gdy $$\Delta < 0$$, pierwiastki są zespolone i oblicza się je przy użyciu wzoru $$x = \frac{-b \pm i\sqrt{|\Delta|}}{2a}$$, gdzie $$i$$ oznacza jednostkę urojoną. Znajomość tych metod jest niezbędna dla każdego, kto chce skutecznie rozwiązywać równania kwadratowe i zrozumieć, jakie rozwiązania można uzyskać w zależności od wartości delty.
Czytaj więcej: Jak pisać równania chemiczne: proste sposoby na poprawne pisanie
Różne metody rozwiązywania równań kwadratowych - porównanie
Znajomość różnych metod rozwiązywania równań kwadratowych jest niezwykle ważna, ponieważ pozwala na elastyczność w podejściu do problemu. Każda metoda ma swoje zalety i wady, a wybór odpowiedniej może zależeć od konkretnego równania oraz preferencji osoby rozwiązującej. Na przykład, metody rozwiązywania równań kwadratowych mogą obejmować faktoryzację, stosowanie wzoru kwadratowego, a także graficzne przedstawienie funkcji kwadratowej. Wiedza o tych różnych podejściach umożliwia szybsze i bardziej efektywne rozwiązywanie problemów matematycznych.
Porównując te metody, warto zauważyć, że każda z nich sprawdza się w różnych sytuacjach. Faktoryzacja jest często szybsza, ale wymaga, aby równanie było łatwe do rozłożenia na czynniki. Z kolei wzór kwadratowy jest uniwersalny i można go stosować w każdym przypadku, ale może być bardziej czasochłonny w obliczeniach. W tabeli poniżej przedstawiono porównanie tych metod, uwzględniając ich główne zalety i wady.
| Metoda | Zalety | Wady |
|---|---|---|
| Faktoryzacja | Szybka, prosta dla łatwych równań | Wymaga umiejętności rozkładu, nie zawsze możliwa |
| Wzór kwadratowy | Uniwersalny, stosowany w każdym przypadku | Może być czasochłonny, wymaga obliczeń |
| Metoda graficzna | Wizualizacja rozwiązań, intuicyjne zrozumienie | Nie zawsze dokładne, wymaga narzędzi graficznych |
Użycie wzoru kwadratowego - kiedy i jak stosować
Wzór kwadratowy jest jednym z najważniejszych narzędzi w rozwiązywaniu równań kwadratowych. Stosuje się go, gdy równanie ma postać $$ax^2 + bx + c = 0$$ i jest szczególnie przydatny w przypadkach, gdy faktoryzacja jest trudna lub niemożliwa. Wzór ten ma postać $$x = \frac{-b \pm \sqrt{\Delta}}{2a}$$, gdzie $$\Delta$$ to delta obliczana ze wzoru $$\Delta = b^2 - 4ac$$. Dzięki temu wzorowi można szybko znaleźć pierwiastki równania, niezależnie od wartości współczynników $$a$$, $$b$$ i $$c$$.
Najlepiej stosować wzór kwadratowy w sytuacjach, gdy delta jest znana, a jej wartość wskazuje na istnienie rozwiązań. Gdy $$\Delta > 0$$, uzyskujemy dwa różne pierwiastki, a gdy $$\Delta = 0$$, jeden pierwiastek podwójny. W przypadku $$\Delta < 0$$, wzór kwadratowy pozwala na uzyskanie pierwiastków zespolonych. Użycie wzoru kwadratowego jest zatem bardzo uniwersalne, co czyni go niezastąpionym narzędziem w matematyce.
Przykłady rozwiązywania równań kwadratowych w praktyce
Rozważmy przykład równania kwadratowego $$2x^2 - 4x - 6 = 0$$. Aby rozwiązać to równanie, najpierw obliczamy deltę: $$\Delta = (-4)^2 - 4 \cdot 2 \cdot (-6) = 16 + 48 = 64$$. Ponieważ $$\Delta > 0$$, możemy zastosować wzór kwadratowy. Podstawiając wartości do wzoru, otrzymujemy: $$x_1 = \frac{4 - \sqrt{64}}{2 \cdot 2} = \frac{4 - 8}{4} = -1$$ oraz $$x_2 = \frac{4 + \sqrt{64}}{2 \cdot 2} = \frac{4 + 8}{4} = 3$$. Zatem pierwiastki równania to $$x_1 = -1$$ oraz $$x_2 = 3$$.
Inny przykład to równanie $$x^2 - 6x + 9 = 0$$, które można łatwo rozwiązać przez faktoryzację. Równanie to można zapisać jako $$(x - 3)^2 = 0$$, co oznacza, że $$x = 3$$ jest pierwiastkiem podwójnym. W tym przypadku faktoryzacja była prostym i szybkim sposobem na znalezienie rozwiązania. Wybór metody zależy od charakterystyki równania, a czasem warto rozważyć obie opcje, aby znaleźć najłatwiejszą drogę do rozwiązania.
Przykład z różnymi wartościami delty (Δ)
Rozważmy równanie kwadratowe $$x^2 - 4x + 3 = 0$$. Aby znaleźć pierwiastki tego równania, najpierw obliczamy deltę: $$\Delta = (-4)^2 - 4 \cdot 1 \cdot 3 = 16 - 12 = 4$$. Ponieważ $$\Delta > 0$$, oznacza to, że równanie ma dwa różne pierwiastki rzeczywiste. Stosując wzór kwadratowy, obliczamy pierwiastki: $$x_1 = \frac{4 - \sqrt{4}}{2} = \frac{4 - 2}{2} = 1$$ oraz $$x_2 = \frac{4 + \sqrt{4}}{2} = \frac{4 + 2}{2} = 3$$. Tak więc pierwiastki równania to $$x_1 = 1$$ oraz $$x_2 = 3$$.
Teraz rozważmy inne równanie, $$x^2 + 2x + 5 = 0$$. Obliczając deltę, otrzymujemy: $$\Delta = (2)^2 - 4 \cdot 1 \cdot 5 = 4 - 20 = -16$$. W tym przypadku $$\Delta < 0$$, co oznacza, że równanie nie ma rozwiązań rzeczywistych, lecz dwa pierwiastki zespolone. Możemy je obliczyć, stosując wzór kwadratowy: $$x = \frac{-2 \pm \sqrt{-16}}{2} = \frac{-2 \pm 4i}{2} = -1 \pm 2i$$. Zatem pierwiastki tego równania to $$x_1 = -1 + 2i$$ oraz $$x_2 = -1 - 2i$$.
Przykłady z zastosowaniem różnych metod rozwiązywania
Rozważmy równanie $$2x^2 - 8x + 6 = 0$$. Możemy je rozwiązać na dwa sposoby: przez faktoryzację i stosując wzór kwadratowy. Najpierw spróbujmy faktoryzacji. Równanie można zapisać jako $$2(x^2 - 4x + 3) = 0$$, co po dalszym rozkładzie daje $$2(x - 3)(x - 1) = 0$$. Zatem pierwiastki to $$x_1 = 3$$ oraz $$x_2 = 1$$.
Teraz zastosujmy wzór kwadratowy do tego samego równania. Obliczamy deltę: $$\Delta = (-8)^2 - 4 \cdot 2 \cdot 6 = 64 - 48 = 16$$. Ponieważ $$\Delta > 0$$, możemy znaleźć pierwiastki: $$x_1 = \frac{8 - \sqrt{16}}{4} = \frac{8 - 4}{4} = 1$$ oraz $$x_2 = \frac{8 + \sqrt{16}}{4} = \frac{8 + 4}{4} = 3$$. Jak widać, obie metody prowadzą do tych samych wyników: $$x_1 = 1$$ oraz $$x_2 = 3$$.
Praktyczne zastosowania równań kwadratowych w różnych dziedzinach
Równania kwadratowe mają szerokie zastosowanie nie tylko w matematyce, ale także w wielu innych dziedzinach, takich jak fizyka, inżynieria czy ekonomia. Na przykład, w fizyce równania kwadratowe mogą być używane do modelowania ruchu ciał, gdzie parametry takie jak prędkość i przyspieszenie mogą być reprezentowane przez równania kwadratowe. Dzięki temu inżynierowie mogą przewidywać trajektorie ruchu obiektów, co jest kluczowe w projektowaniu systemów takich jak rakiety czy pojazdy autonomiczne.
W ekonomii, równania kwadratowe są wykorzystywane do analizy kosztów i przychodów, co pozwala na optymalizację zysków. Przykładowo, przedsiębiorcy mogą używać równań kwadratowych do określenia punktu, w którym przychody pokrywają koszty, co jest istotne dla podejmowania decyzji biznesowych. W przyszłości, z rozwojem technologii, takich jak sztuczna inteligencja, wykorzystanie równań kwadratowych w analizach danych oraz prognozowaniu trendów rynkowych będzie się tylko zwiększać, co czyni tę umiejętność jeszcze bardziej wartościową.