Sinus to kluczowy pojęcie w matematyce, szczególnie w kontekście trójkątów prostokątnych. W najprostszych słowach, sinus kąta ostrego jest stosunkiem długości przyprostokątnej leżącej naprzeciwko tego kąta do długości przeciwprostokątnej. Zrozumienie tej definicji jest fundamentem dla dalszego zgłębiania tematu, ponieważ sinus odgrywa istotną rolę w wielu obszarach matematyki i nauk przyrodniczych.
W artykule przyjrzymy się nie tylko definicji sinusa, ale także jego zastosowaniom oraz sposobom obliczania wartości tego funkcji w praktyce. Poznamy wzór na sinus, a także zobaczymy, jak można go wykorzystać w różnych dziedzinach, takich jak inżynieria czy architektura.
Kluczowe informacje:- Sinus kąta ostrego to stosunek długości przyprostokątnej do długości przeciwprostokątnej.
- Wzór na sinus to sin(α) = a/c, gdzie a to długość przyprostokątnej, a c to długość przeciwprostokątnej.
- Obliczanie sinusa jest kluczowe w trójkątach prostokątnych i ma zastosowanie w różnych dziedzinach.
- Sinus znajduje zastosowanie w inżynierii, architekturze oraz naukach przyrodniczych.
- Wiedza o sinusa jest niezbędna do zrozumienia bardziej zaawansowanych zagadnień matematycznych.
Co to jest sinus i jego definicja w matematyce?
Sinus jest fundamentalnym pojęciem w matematyce, szczególnie w dziedzinie trigonometrii. Definiuje się go jako stosunek długości przyprostokątnej leżącej naprzeciwko kąta do długości przeciwprostokątnej w trójkącie prostokątnym. Ta definicja jest kluczowa, ponieważ pozwala zrozumieć, jak sinus odnosi się do kątów i długości boków w trójkątach.
Sinus odgrywa istotną rolę w wielu zastosowaniach matematycznych oraz inżynieryjnych. Poznanie jego definicji oraz znaczenia w kontekście kątów ostrogi jest niezbędne dla dalszego zgłębiania zagadnień związanych z trójkątami i ich właściwościami. Dzięki sinusowi można łatwiej obliczać różne wartości i rozwiązywać problemy geometryczne.
Zrozumienie sinusa kąta ostrego w kontekście trójkątów
Sinus kąta ostrego jest ściśle związany z trójkątami prostokątnymi. W takim trójkącie, jeśli mamy kąt ostry, to jego sinus można zdefiniować jako stosunek długości boku naprzeciwko tego kąta do długości przeciwprostokątnej. Oznacza to, że sinus kąta pozwala określić, jak "wysoko" znajdujemy się w trójkącie w stosunku do długości jego najdłuższego boku, czyli przeciwprostokątnej.
W praktyce, zrozumienie tej relacji jest kluczowe, ponieważ umożliwia obliczenia związane z kątami i bokami trójkątów. Dzięki temu, możemy wykorzystać sinus do rozwiązywania różnych problemów matematycznych oraz inżynieryjnych, gdzie trójkąty odgrywają istotną rolę. Warto zauważyć, że sinus jest funkcją, która zmienia się w zależności od wartości kąta, co czyni ją niezwykle użyteczną w różnych dziedzinach.
Wzór na sinus i jego zastosowanie w obliczeniach
Wzór na sinus jest kluczowym elementem w trigonometrii, który pozwala na obliczanie wartości sinusa kąta. Definiuje się go jako sin(α) = a/c, gdzie a to długość przyprostokątnej leżącej naprzeciwko kąta α, a c to długość przeciwprostokątnej. Dzięki temu wzorowi można łatwo określić wartość sinusa dla danego kąta, co jest niezwykle przydatne w wielu obliczeniach matematycznych.
Znajomość tego wzoru jest niezbędna w różnych dziedzinach, takich jak geometria, inżynieria czy fizyka. Umożliwia on nie tylko obliczenia w trójkątach prostokątnych, ale także w bardziej złożonych problemach, gdzie trigonometryczne funkcje odgrywają kluczową rolę. Obliczanie sinusa stanowi fundament dla dalszych badań i aplikacji w naukach ścisłych.
Jak obliczyć sinus kąta w trójkącie prostokątnym?
Obliczanie sinusa kąta w trójkącie prostokątnym jest procesem, który można przeprowadzić w kilku prostych krokach. Po pierwsze, należy zidentyfikować kąt, dla którego chcemy obliczyć sinus, a następnie zmierzyć długości odpowiednich boków trójkąta: przyprostokątnej naprzeciwko kąta oraz przeciwprostokątnej. Używając wzoru sin(α) = a/c, można łatwo obliczyć wartość sinusa.
W praktyce, znajomość metod obliczania sinusa jest niezbędna w różnych zastosowaniach, od rozwiązywania problemów geometrycznych po zastosowania inżynieryjne. Dzięki tym technikom, można skutecznie wykorzystać sinus w codziennych obliczeniach i projektach.
Przykłady obliczeń sinusa dla różnych kątów
Obliczanie sinusa dla różnych kątów jest kluczowym elementem w trigonometrii. Rozpocznijmy od kąta 30°. W trójkącie prostokątnym, gdzie kąt α wynosi 30°, sinus tego kąta jest równy 0,5. Oznacza to, że stosunek długości przyprostokątnej naprzeciwko kąta do długości przeciwprostokątnej wynosi 1:2. Dzięki temu możemy łatwo obliczyć długość boku naprzeciwko kąta, znając długość przeciwprostokątnej.
Kolejnym przykładem jest kąt 45°. W tym przypadku sinus kąta 45° wynosi √2/2, co oznacza, że długości obu przyprostokątnych są równe, a ich stosunek do przeciwprostokątnej wynosi 1:√2. To właściwość, która sprawia, że trójkąty o kącie 45° są często stosowane w praktycznych zastosowaniach, takich jak budownictwo czy projektowanie.
| Kąt (°) | Sinus | Przyprostokątna (a) | Przeciwprostokątna (c) |
|---|---|---|---|
| 30 | 0,5 | 1 | 2 |
| 45 | √2/2 | 1 | √2 |
| 60 | √3/2 | √3 | 2 |
| 90 | 1 | Przeciwprostokątna | Przeciwprostokątna |
Graficzna ilustracja sinusa w trójkącie prostokątnym
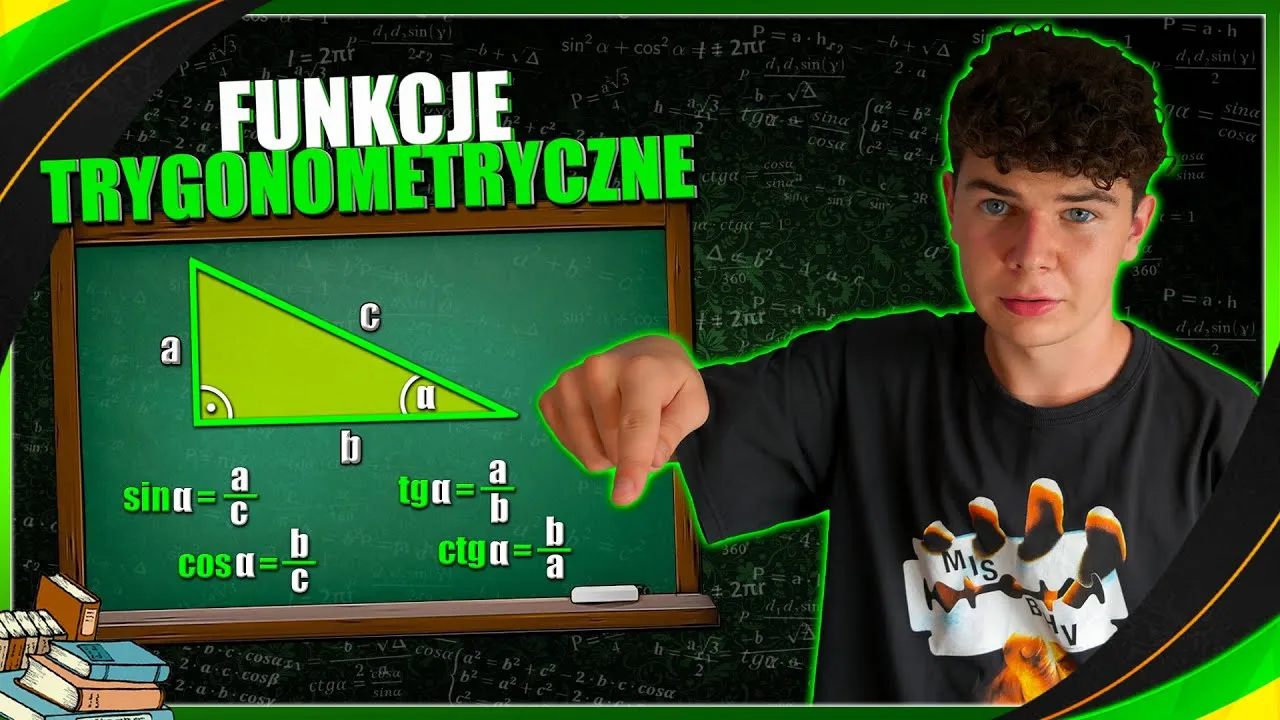
Graficzne przedstawienie sinusa w trójkącie prostokątnym jest niezwykle pomocne w zrozumieniu tej funkcji. W diagramie trójkąta prostokątnego możemy zobaczyć, jak sinus kąta ostrego α jest zdefiniowany jako stosunek długości przyprostokątnej naprzeciwko kąta do długości przeciwprostokątnej. Wizualizacja tego stosunku pozwala lepiej zrozumieć, jak zmiana kąta wpływa na wartość sinusa oraz jak wygląda relacja między bokami trójkąta.
Na przykład, w trójkącie prostokątnym z kątem α, długość boku naprzeciwko kąta jest oznaczona jako a, a długość przeciwprostokątnej jako c. W miarę zmiany kąta α, długość boku naprzeciwko kąta zmienia się, co wpływa na wartość sinusa. Graficzne przedstawienia sinusa są również przydatne w naukach inżynieryjnych, gdzie pozwalają na szybkie zrozumienie i obliczenie wartości kątów i długości boków w różnych zastosowaniach.
Czytaj więcej: Rzemieślnicza Zasadnicza Szkoła Zawodowa im. S. Palucha: Edukacja z pasją
Zastosowanie sinusa w praktyce i codziennym życiu
Sinus ma szerokie zastosowanie w wielu dziedzinach, takich jak inżynieria, fizyka czy architektura. W praktyce, znajomość sinusa jest niezbędna do obliczeń związanych z kątami i długościami boków w trójkątach prostokątnych, co jest kluczowe w projektowaniu budynków, mostów oraz innych konstrukcji. Dzięki funkcji sinus można również obliczać wysokości obiektów oraz odległości w trudnych warunkach terenowych.
W codziennym życiu, sinus jest używany w różnych technologiach, takich jak systemy nawigacyjne, gdzie obliczenia kątów są niezbędne do określenia pozycji. Rozumienie sinusa i jego zastosowań pozwala na lepsze podejmowanie decyzji w projektach technicznych oraz naukowych, co czyni go nieocenionym narzędziem w naukach ścisłych.
Sinus w inżynierii i architekturze: przykłady zastosowań
W inżynierii, sinus odgrywa kluczową rolę w obliczeniach związanych z projektowaniem struktur. Na przykład, inżynierowie często wykorzystują sinus do obliczania kątów nachylenia ramp, schodów czy dachów. Dzięki funkcji sinus, mogą precyzyjnie określić, jakie muszą być wymiary danego elementu, aby zapewnić bezpieczeństwo i stabilność konstrukcji. W projekcie mostu, znajomość sinusa pozwala na obliczenie sił działających na poszczególne elementy, co jest kluczowe dla ich prawidłowego zaprojektowania.
W architekturze, sinus jest używany do obliczania wysokości budynków oraz odległości między różnymi punktami w przestrzeni. Na przykład, architekci mogą wykorzystać sinus do określenia wysokości dachu w stosunku do długości ściany. To pozwala na stworzenie estetycznych i funkcjonalnych projektów, które będą jednocześnie stabilne. Dzięki zastosowaniu sinusa, architekci są w stanie lepiej planować przestrzeń i dostosowywać projekty do wymagań klientów.
Rola sinusa w naukach przyrodniczych i technologii
W naukach przyrodniczych, sinus ma istotne zastosowanie w fizyce, szczególnie w obliczeniach związanych z falami i drganiami. Na przykład, sinus pojawia się w równaniach falowych, które opisują ruch fal dźwiękowych czy elektromagnetycznych. W technologii, sinus jest wykorzystywany w systemach nawigacyjnych, gdzie obliczenia kątów są niezbędne do określenia pozycji obiektów. Dzięki zastosowaniu sinusa, inżynierowie mogą tworzyć bardziej precyzyjne urządzenia i technologie, które wykorzystują fale, takie jak radary czy systemy GPS.
Nowe technologie i przyszłość zastosowań sinusa w naukach
W miarę jak technologia się rozwija, sinus znajduje coraz szersze zastosowanie w nowoczesnych dziedzinach, takich jak sztuczna inteligencja i uczenie maszynowe. Algorytmy te często wykorzystują funkcje trygonometryczne, w tym sinus, do analizy danych i rozpoznawania wzorców. Na przykład, w przetwarzaniu sygnałów audio i wideo, sinus jest kluczowy w algorytmach kompresji, które pozwalają na efektywne przesyłanie informacji bez utraty jakości.
Dodatkowo, w kontekście rozwoju technologii VR i AR (wirtualnej i rozszerzonej rzeczywistości), sinus odgrywa ważną rolę w obliczeniach kątów widzenia i przekształceniach przestrzennych. Dzięki zastosowaniu sinusa, programiści mogą tworzyć bardziej realistyczne i immersyjne środowiska, które lepiej odwzorowują rzeczywistość. W przyszłości możemy spodziewać się jeszcze szerszego zastosowania sinusa w analizie danych z sensorów, co zrewolucjonizuje wiele branż, od medycyny po inżynierię.