Czy cosinus może być ujemny? To pytanie, które często pojawia się w kontekście trigonometrii i analizy funkcji trygonometrycznych. Odpowiedź brzmi: tak, cosinus może przyjmować wartości ujemne. Zrozumienie, w jakich sytuacjach to następuje, jest kluczowe dla każdego, kto chce zgłębić temat układu współrzędnych i funkcji trygonometrycznych.
W układzie współrzędnych, wartości cosinusa zmieniają się w zależności od ćwiartki, w której się znajdujemy. W drugiej ćwiartce cosinus jest ujemny, podczas gdy sinus pozostaje dodatni. W trzeciej ćwiartce zarówno sinus, jak i cosinus przyjmują wartości ujemne. Warto zatem przyjrzeć się bliżej tym wartościom, aby lepiej zrozumieć, jak działają funkcje trygonometryczne.
Kluczowe wnioski:- Cosinus może być ujemny, co jest szczególnie widoczne w drugiej i trzeciej ćwiartce układu współrzędnych.
- W drugiej ćwiartce sinus jest dodatni, a cosinus ujemny.
- W trzeciej ćwiartce zarówno sinus, jak i cosinus są ujemne.
- W pierwszej ćwiartce wartości cosinusa są zawsze dodatnie.
- W czwartej ćwiartce cosinus powraca do wartości dodatnich.
Cosinus i jego wartości: Czy może być ujemny?
Cosinus, jako jedna z podstawowych funkcji trygonometrycznych, odgrywa kluczową rolę w matematyce. Może przyjmować wartości ujemne, co jest istotne dla zrozumienia jego zachowania w różnych kontekstach. Wartości cosinusa zmieniają się w zależności od kąta, a jego zakres wynosi od -1 do 1. W szczególności, ujemne wartości cosinusa występują w określonych ćwiartkach układu współrzędnych, co jest kluczowe dla analizy funkcji trygonometrycznych.
W kontekście funkcji cosinus, zrozumienie, kiedy i dlaczego przyjmuje wartości ujemne, jest fundamentalne dla każdego, kto chce zgłębić temat trygonometrii. W kolejnych sekcjach omówimy, jak wartości cosinusa różnią się w różnych ćwiartkach układu współrzędnych, a także jakie mają znaczenie w praktycznych zastosowaniach.
Zrozumienie funkcji cosinus w kontekście wartości ujemnych
Funkcja cosinus jest zdefiniowana jako stosunek długości przyprostokątnej przyległej do kąta do długości przeciwprostokątnej w trójkącie prostokątnym. Wartości cosinusa są szczególnie ważne w kontekście analizy kątów w układzie współrzędnych. Wartości te mogą być dodatnie lub ujemne, w zależności od kąta, który analizujemy. Na przykład, cosinus kąta 0° wynosi 1, podczas gdy dla kąta 180° wynosi -1.Wartości ujemne cosinusa pojawiają się, gdy kąt znajduje się w drugiej lub trzeciej ćwiartce układu współrzędnych. W drugiej ćwiartce, cosinus jest ujemny, podczas gdy sinus pozostaje dodatni. W trzeciej ćwiartce zarówno sinus, jak i cosinus przyjmują wartości ujemne. Zrozumienie tych zasad jest kluczowe dla dalszej analizy funkcji trygonometrycznych.
Wpływ ćwiartek układu współrzędnych na wartości cosinusa
Układ współrzędnych dzieli płaszczyznę na cztery ćwiartki, co ma istotny wpływ na wartości funkcji trygonometrycznych, w tym cosinusa. W pierwszej ćwiartce zarówno sinus, jak i cosinus są dodatnie. W drugiej ćwiartce cosinus staje się ujemny, co oznacza, że wartości kątów między 90° a 180° prowadzą do ujemnych wyników. W trzeciej ćwiartce, wartości cosinusa są również ujemne, co jest zgodne z tym, że zarówno sinus, jak i cosinus przyjmują wartości ujemne w tym zakresie kątów.
W czwartej ćwiartce, cosinus znowu staje się dodatni, co pokazuje, że zmiany wartości cosinusa są ściśle związane z położeniem kąta w układzie współrzędnych. Zrozumienie, jak te wartości zmieniają się w różnych ćwiartkach, jest kluczowe dla analizy funkcji trygonometrycznych i ich zastosowań w praktycznych problemach matematycznych.
Analiza wartości cosinusa w różnych ćwiartkach
Wartości cosinusa zmieniają się w zależności od ćwiartki, w której znajduje się kąt. W różnych ćwiartkach układu współrzędnych cosinus może przyjmować zarówno wartości dodatnie, jak i ujemne. W tej sekcji przyjrzymy się, jak te wartości są zróżnicowane w każdej ćwiartce, zwracając szczególną uwagę na sytuacje, kiedy cosinus może być ujemny.
W pierwszej ćwiartce kąt znajduje się między 0° a 90°, a wartości cosinusa są zawsze dodatnie. W drugiej ćwiartce, która obejmuje kąty od 90° do 180°, cosinus staje się ujemny. W trzeciej ćwiartce, kąt od 180° do 270° również prowadzi do ujemnych wartości cosinusa. W czwartej ćwiartce, od 270° do 360°, wartości cosinusa znowu stają się dodatnie. Poniżej przedstawimy szczegółowe analizy dla każdej z ćwiartek.
Wartości cosinusa w pierwszej ćwiartce: zawsze dodatnie
W pierwszej ćwiartce układu współrzędnych, gdzie kąt mieści się w zakresie od 0° do 90°, wartości cosinusa są zawsze dodatnie. Oznacza to, że dla każdego kąta w tym zakresie, cosinus przyjmuje wartości od 1 do 0. Na przykład, dla kąta 0° cosinus wynosi 1, a dla kąta 90° wynosi 0. Wartości te są istotne w wielu zastosowaniach, takich jak obliczenia w geometrii czy fizyce.
Wartości cosinusa w drugiej ćwiartce: co oznacza ujemny cosinus?
W drugiej ćwiartce, obejmującej kąty od 90° do 180°, cosinus przyjmuje wartości ujemne. Oznacza to, że dla kątów w tym zakresie, takich jak 120° czy 150°, wartości cosinusa będą wynosić odpowiednio -0,5 i -0,87. Wartości te są kluczowe dla zrozumienia, dlaczego cosinus może być ujemny, co ma istotne znaczenie w kontekście analizy funkcji trygonometrycznych.
- Kąt 90°: cosinus = 0
- Kąt 120°: cosinus = -0,5
- Kąt 150°: cosinus = -0,87
Wartości cosinusa w trzeciej ćwiartce: zarówno ujemny, jak i sinus
W trzeciej ćwiartce układu współrzędnych, gdzie kąty wahają się od 180° do 270°, zarówno cosinus, jak i sinus przyjmują wartości ujemne. To oznacza, że dla kątów takich jak 210° czy 240°, wartości cosinusa będą wynosić odpowiednio -0,87 i -0,5. Ujemne wartości cosinusa w tym zakresie są istotne dla zrozumienia, jak funkcje trygonometryczne działają w praktyce.
Wartości ujemne cosinusa w trzeciej ćwiartce mają wiele zastosowań, zwłaszcza w kontekście obliczeń geometrycznych i trygonometrycznych. Na przykład, dla kąta 225°, cosinus wynosi -0,71, co pokazuje, jak zmieniają się wartości w tej ćwiartce. Zrozumienie tych zasad jest kluczowe dla analizy funkcji trygonometrycznych oraz ich zastosowań w różnych dziedzinach nauki.
Wartości cosinusa w czwartej ćwiartce: powrót do dodatnich wartości
W czwartej ćwiartce, obejmującej kąty od 270° do 360°, cosinus znowu przyjmuje wartości dodatnie. Oznacza to, że dla kątów takich jak 300° czy 330°, wartości cosinusa będą wynosić odpowiednio 0,5 i 0,87. Wartości te są istotne, ponieważ pokazują, jak funkcje trygonometryczne zmieniają się w zależności od położenia kąta w układzie współrzędnych.
W czwartej ćwiartce, cosinus osiąga swoje maksymalne wartości dodatnie, co jest zgodne z intuicją, że im bliżej kąta 360°, tym wartości cosinusa są wyższe. Zrozumienie tych aspektów jest kluczowe dla skutecznych obliczeń w trigonometrii oraz w zastosowaniach praktycznych, takich jak analiza fal czy modelowanie zjawisk fizycznych.
Czytaj więcej: Kreatywne zabawy z przedszkolakami: 15 pomysłów na rozwój malucha
Praktyczne zastosowania: Jak wykorzystać wiedzę o cosinusie?
Wiedza na temat wartości cosinusa ma wiele praktycznych zastosowań, zwłaszcza w dziedzinie trygonometrii. Zrozumienie, jak i kiedy cosinus może być ujemny, jest kluczowe w rozwiązywaniu różnych problemów matematycznych i inżynieryjnych. W tej sekcji omówimy konkretne przykłady zastosowania wartości cosinusa w zadaniach trigonometrycznych oraz ich znaczenie w praktyce.
Jednym z głównych zastosowań cosinusa jest obliczanie długości boków i kątów w trójkątach. Dzięki funkcji cosinus można łatwo określić, jakie wartości przyjmują boki w zależności od kątów. Wartości ujemne cosinusa są szczególnie ważne w przypadku analizy kątów w drugiej i trzeciej ćwiartce, gdzie mogą pojawić się ujemne wyniki. Poniżej przedstawiamy kilka przykładów zastosowania wartości cosinusa w praktyce.
Przykłady zastosowania cosinusa w zadaniach trigonometrycznych
Wartości cosinusa są powszechnie wykorzystywane w różnych zadaniach trigonometrycznych, takich jak obliczanie wysokości budynków, odległości czy kątów. Na przykład, w zadaniu dotyczącym obliczania wysokości drzewa, można użyć funkcji cosinus, aby znaleźć wysokość, gdy znane są odległość od drzewa oraz kąt widzenia. Innym przykładem może być obliczanie odległości między punktami na mapie, gdzie również wykorzystuje się wartości cosinusa.
- Obliczanie wysokości drzewa na podstawie odległości i kąta widzenia.
- Analiza odległości między punktami na mapie przy użyciu funkcji cosinus.
- Obliczenia w inżynierii, takie jak projektowanie konstrukcji budowlanych.
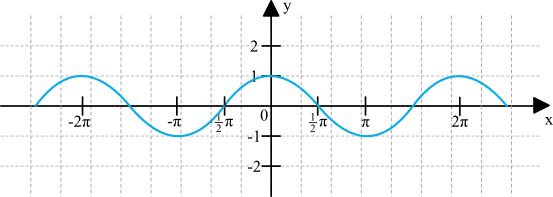
Jak zrozumienie wartości ujemnych cosinusa wpływa na obliczenia
Rozpoznawanie ujemnych wartości cosinusa jest kluczowe dla dokładności obliczeń w różnych zadaniach matematycznych. Kiedy zrozumiemy, w jakich sytuacjach cosinus przyjmuje wartości ujemne, możemy lepiej interpretować wyniki i unikać błędów w obliczeniach. Na przykład, w kontekście kątów w drugiej i trzeciej ćwiartce, wartości ujemne mają istotne znaczenie dla analizy trójkątów i obliczeń w geometrii.
W praktyce, uwzględnienie ujemnych wartości cosinusa pozwala na poprawne obliczenia w zadaniach wymagających analizy kątów, takich jak obliczenia wysokości, odległości czy projektowanie konstrukcji. Ignorowanie tych wartości może prowadzić do błędnych wyników, co w konsekwencji wpływa na dalsze etapy obliczeń. Dlatego warto zawsze mieć na uwadze, w jakich ćwiartkach cosinus jest ujemny i jak to wpływa na wyniki naszych obliczeń.
Jak wykorzystać wartości cosinusa w analizie fal i sygnałów
Wartości cosinusa mają kluczowe znaczenie nie tylko w geometrii, ale także w analizie fal i sygnałów, co staje się coraz bardziej istotne w dziedzinach takich jak inżynieria dźwięku i telekomunikacja. Na przykład, w analizie sygnałów, funkcje trygonometryczne, w tym cosinus, są wykorzystywane do opisu fal sinusoidalnych, które są podstawą wielu technologii, takich jak modulacja amplitudy i częstotliwości. Zrozumienie, jak ujemne wartości cosinusa wpływają na kształt fali, może pomóc inżynierom w optymalizacji systemów komunikacyjnych.
W praktyce, umiejętność manipulacji wartościami cosinusa w kontekście analizy sygnałów pozwala na lepsze zrozumienie, jak różne zmienne wpływają na jakość transmisji. Na przykład, w systemach radarowych, wartości cosinusa są używane do określenia kątów odbicia fal, co jest kluczowe dla precyzyjnego lokalizowania obiektów. W przyszłości, rozwój technologii związanych z analizą sygnałów będzie coraz bardziej zależał od zrozumienia i wykorzystania funkcji trygonometrycznych, co otworzy nowe możliwości w dziedzinach takich jak sztuczna inteligencja i Internet rzeczy (IoT).

