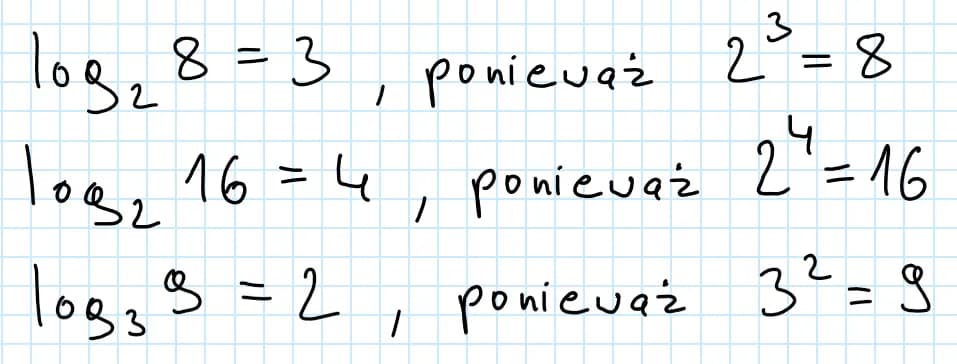Logarytmy to ważny temat w matematyce, który pozwala zrozumieć relacje między liczbami w kontekście potęg. Obliczanie logarytmów może wydawać się skomplikowane, ale w rzeczywistości opiera się na prostej definicji. Logarytm liczby $$b$$ przy podstawie $$a$$, oznaczany jako $$\log_a b$$, to wykładnik potęgi, do jakiej należy podnieść podstawę $$a$$, aby uzyskać liczbę $$b$$. W tym artykule przedstawimy, jak obliczać logarytmy krok po kroku, a także omówimy ich właściwości i zastosowania.
W kolejnych sekcjach skupimy się na praktycznych metodach obliczania logarytmów dla różnych podstaw, a także na przykładach, które pomogą w lepszym zrozumieniu tego zagadnienia. Dzięki temu każdy, niezależnie od poziomu zaawansowania, będzie mógł łatwo nauczyć się, jak posługiwać się logarytmami w codziennych obliczeniach.
Najważniejsze informacje:
- Logarytm $$\log_a b$$ to wykładnik potęgi, który spełnia równanie $$a^x = b$$.
- Obliczanie logarytmu polega na przekształceniu równania do postaci, w której można porównać wykładniki potęg.
- Wzór na zmianę podstawy logarytmu to $$\log_a b = \frac{\log_c b}{\log_c a}$$, co ułatwia obliczenia przy użyciu kalkulatorów.
- Istnieją istotne własności logarytmów, takie jak: $$\log_a (b \cdot c) = \log_a b + \log_a c$$ oraz $$\log_a \left(\frac{b}{c}\right) = \log_a b - \log_a c$$.
- Logarytmy mają zastosowanie w różnych dziedzinach, w tym w matematyce, fizyce i biologii, co czyni je niezwykle użytecznymi w analizie danych i rozwiązywaniu problemów.
Jak obliczyć logarytmy? Prosta definicja i zasady działania
Logarytmy to kluczowy element matematyki, który pomaga zrozumieć, jak liczby są ze sobą powiązane. Obliczanie logarytmów może wydawać się skomplikowane, ale w rzeczywistości opiera się na prostej definicji. Logarytm liczby $$b$$ przy podstawie $$a$$, zapisany jako $$\log_a b$$, to wartość $$x$$, która spełnia równanie $$a^x = b$$. Wartości podstawy $$a$$ muszą być większe od zera i różne od jedności, a liczba $$b$$ musi być dodatnia. Logarytmy są niezwykle ważne w wielu dziedzinach, takich jak nauki przyrodnicze, inżynieria czy ekonomia. Logarytmy pozwalają na przekształcanie skomplikowanych obliczeń potęgowych w prostsze operacje dodawania i odejmowania. Dzięki nim można łatwiej analizować dane oraz rozwiązywać równania, które w inny sposób byłyby trudne do uchwycenia. W kolejnych sekcjach przyjrzymy się bliżej, jak obliczać logarytmy oraz jakie mają one właściwości, które ułatwiają ich stosowanie w praktyce.Czym jest logarytm i jak go zdefiniować?
Logarytm to funkcja, która odpowiada na pytanie: jaką potęgę należy przyjąć dla danej podstawy, aby uzyskać określoną liczbę? W matematycznej notacji, logarytm liczby $$b$$ przy podstawie $$a$$ to $$\log_a b$$. Wartość logarytmu można interpretować jako wykładnik potęgi, do jakiej należy podnieść podstawę $$a$$, aby otrzymać liczbę $$b$$. Na przykład, $$\log_2 8$$ oznacza, że szukamy takiego wykładnika $$x$$, dla którego $$2^x = 8$$.
Logarytmy mają swoje zastosowanie w różnych obszarach matematyki i nauki. Umożliwiają one przekształcanie równań i rozwiązywanie problemów, które mogą być zbyt złożone do analizy bez użycia tej funkcji. Zrozumienie logarytmów jest kluczowe dla dalszego zgłębiania tematów takich jak analiza matematyczna, statystyka czy algebra.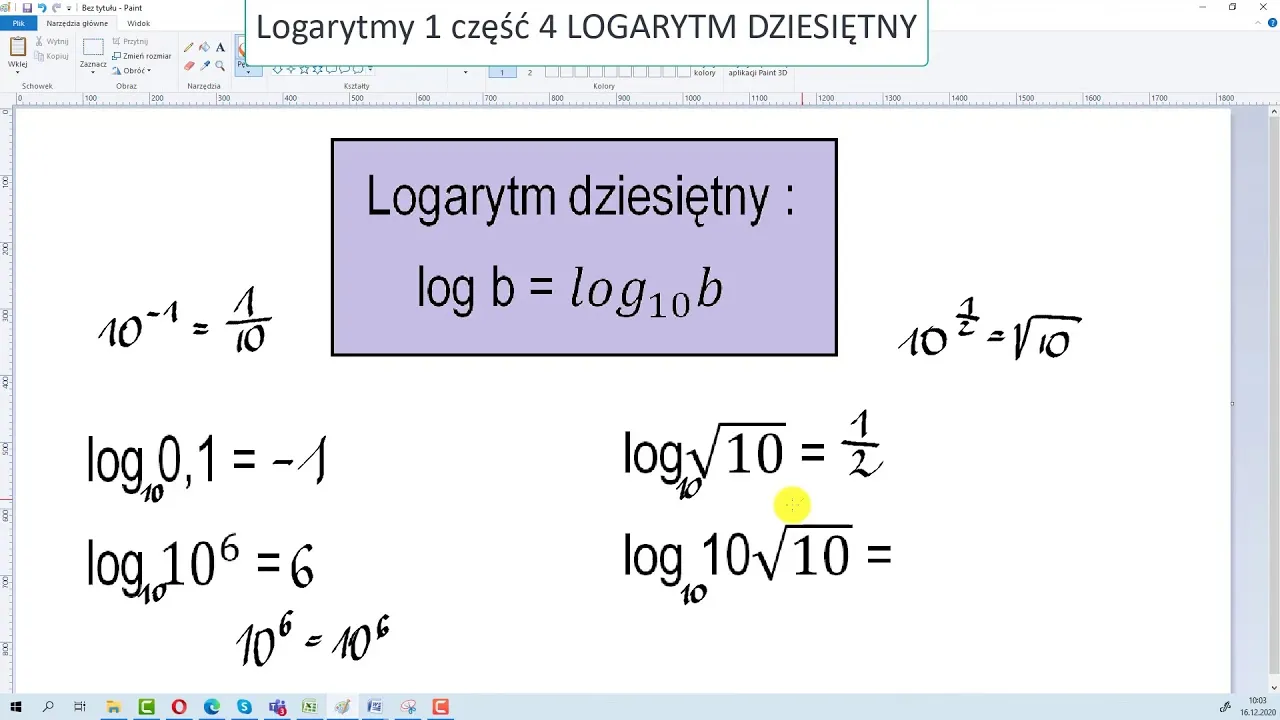
Krok po kroku: Jak obliczać logarytmy dla różnych podstaw?
Aby obliczyć logarytmy, należy postępować zgodnie z określonymi krokami, które ułatwiają zrozumienie procesu. Niezależnie od tego, czy obliczamy logarytm przy podstawie 2, 10 czy innej, podstawowe zasady pozostają takie same. Kluczowe jest, aby zacząć od zapisania równania w formie $$a^x = b$$, gdzie $$a$$ to podstawa, $$b$$ to liczba, której logarytm chcemy obliczyć, a $$x$$ to wynik, którego szukamy. W kolejnych krokach przekształcamy równania i porównujemy wykładniki potęg, aby znaleźć wartość $$x$$.
Obliczanie logarytmu można przeprowadzić w kilku prostych krokach:
- Oznacz wynik logarytmu jako niewiadomą, np. $$x$$.
- Zapisz równanie zgodnie z definicją: $$a^x = b$$.
- Przekształć obie strony równania do tej samej podstawy potęgi, jeśli to możliwe.
- Porównaj wykładniki potęg, ponieważ jeśli podstawy są równe, to i wykładniki muszą być równe.
- Rozwiąż równanie względem $$x$$, co daje wartość logarytmu.
Przykład obliczania logarytmu przy podstawie 2
Rozważmy przykład obliczenia $$\log_2 8$$. Zaczynamy od oznaczenia wyniku jako $$x$$, więc mamy $$\log_2 8 = x$$. Następnie zapisujemy równanie, które z definicji logarytmu wygląda tak: $$2^x = 8$$. Teraz przekształcamy liczbę 8 do postaci potęgi o podstawie 2: $$8 = 2^3$$. W rezultacie mamy $$2^x = 2^3$$, co oznacza, że $$x = 3$$. Zatem wynik to $$\log_2 8 = 3$$.
- Potęgi liczby 2: $$2^0 = 1$$, $$2^1 = 2$$, $$2^2 = 4$$, $$2^3 = 8$$, $$2^4 = 16$$.
- Logarytmy przy podstawie 2 są często używane w informatyce, na przykład w analizie złożoności algorytmów.
- Obliczenia logarytmiczne są przydatne w różnych dziedzinach, takich jak statystyka czy inżynieria.
Obliczanie logarytmu przy podstawie 10 – praktyczne wskazówki
Logarytmy przy podstawie 10, znane również jako logarytmy dziesiętne, są powszechnie stosowane w różnych dziedzinach, takich jak nauki ścisłe, inżynieria czy finanse. Aby obliczyć logarytm przy podstawie 10, można wykorzystać prostą definicję: $$\log_{10} b$$ to wykładnik potęgi, do jakiej należy podnieść 10, aby uzyskać liczbę $$b$$. Przykładowo, $$\log_{10} 100 = 2$$, ponieważ $$10^2 = 100$$. Logarytmy dziesiętne są szczególnie przydatne w analizach danych, ponieważ umożliwiają łatwe porównywanie wartości w skali logarytmicznej.
W praktyce, logarytmy przy podstawie 10 są często używane w obliczeniach związanych z pH w chemii, w analizie danych statystycznych czy w obliczeniach finansowych, takich jak obliczanie odsetek. Użycie kalkulatorów, które automatycznie obliczają logarytmy dziesiętne, ułatwia pracę i przyspiesza proces analizy. Warto pamiętać, że logarytmy dziesiętne są także dostępne w arkuszach kalkulacyjnych, co sprawia, że są one jeszcze bardziej dostępne dla osób zajmujących się analizą danych.
Jak wykorzystać wzory logarytmiczne do szybkich obliczeń?
Wzory logarytmiczne są niezwykle pomocne w obliczaniu logarytmów i mogą znacznie uprościć proces obliczeń. Istnieją trzy podstawowe zasady, które warto znać: po pierwsze, logarytm iloczynu mówi, że $$\log_a (b \cdot c) = \log_a b + \log_a c$$. To oznacza, że logarytm z iloczynu dwóch liczb jest równy sumie ich logarytmów. Po drugie, logarytm ilorazu stwierdza, że $$\log_a \left(\frac{b}{c}\right) = \log_a b - \log_a c$$, co pozwala na łatwe odejmowanie logarytmów. Po trzecie, logarytm potęgi wyraża się jako $$\log_a (b^c) = c \cdot \log_a b$$, co ułatwia obliczenia, gdy mamy do czynienia z potęgami.
Znajomość tych wzorów pozwala na szybkie przekształcanie skomplikowanych obliczeń w prostsze operacje. Dzięki nim można łatwo obliczać logarytmy w różnych kontekstach, co jest szczególnie przydatne w naukach ścisłych, finansach czy inżynierii. Warto również pamiętać, że korzystanie z kalkulatorów, które obsługują te wzory, może znacznie przyspieszyć proces obliczeń i poprawić dokładność wyników.
| Własność logarytmu | Formuła | Przykład |
|---|---|---|
| Logarytm iloczynu | $$\log_a (b \cdot c) = \log_a b + \log_a c$$ | $$\log_2 (4 \cdot 8) = \log_2 4 + \log_2 8$$ |
| Logarytm ilorazu | $$\log_a \left(\frac{b}{c}\right) = \log_a b - \log_a c$$ | $$\log_3 \left(\frac{27}{9}\right) = \log_3 27 - \log_3 9$$ |
| Logarytm potęgi | $$\log_a (b^c) = c \cdot \log_a b$$ | $$\log_5 (25^2) = 2 \cdot \log_5 25$$ |
Zastosowanie logarytmów w matematyce i naukach przyrodniczych
Logarytmy mają szerokie zastosowanie w różnych dziedzinach, w tym w matematyce, fizyce oraz biologii. W matematyce logarytmy są używane do rozwiązywania równań wykładniczych oraz w analizie funkcji. W fizyce logarytmy pomagają w opisywaniu zjawisk, takich jak skala pH, która jest logarytmiczną miarą stężenia jonów wodoru w roztworze. W biologii logarytmy są wykorzystywane do modelowania wzrostu populacji oraz w analizach statystycznych, aby lepiej zrozumieć dane.
W praktyce, logarytmy są także niezbędne w inżynierii, gdzie pomagają w obliczeniach związanych z poziomem dźwięku (skala decybeli) oraz w analizie danych w naukach przyrodniczych. Ich umiejętne wykorzystanie pozwala na efektywne przetwarzanie i interpretację danych, co jest kluczowe w badaniach naukowych oraz w praktycznych zastosowaniach technologicznych.
Jak logarytmy wspierają rozwój technologii i analizy danych
Logarytmy odgrywają kluczową rolę w nowoczesnych technologiach i analizie danych, szczególnie w kontekście big data i uczenia maszynowego. W miarę jak ilość danych rośnie, umiejętność ich efektywnego przetwarzania staje się coraz bardziej istotna. Logarytmy pozwalają na normalizację danych, co jest niezbędne do porównywania różnych zestawów danych o różnych jednostkach i skalach. Na przykład, w analizach statystycznych logarytmy mogą pomóc w przekształceniu rozkładów o dużych wartościach odstających, co prowadzi do bardziej stabilnych i wiarygodnych modeli predykcyjnych.Dodatkowo, w kontekście programowania i algorytmów, logarytmy są wykorzystywane w wielu zaawansowanych technikach, takich jak algorytmy wyszukiwania i sortowania, które optymalizują czas wykonania operacji. Na przykład, algorytmy oparte na drzewach binarnych wykorzystują logarytmy do określenia efektywności wyszukiwania, co jest kluczowe w aplikacjach wymagających szybkiego dostępu do danych. W przyszłości, z rosnącym znaczeniem sztucznej inteligencji i analizy danych, umiejętność wykorzystania logarytmów w tych dziedzinach stanie się jeszcze bardziej istotna.