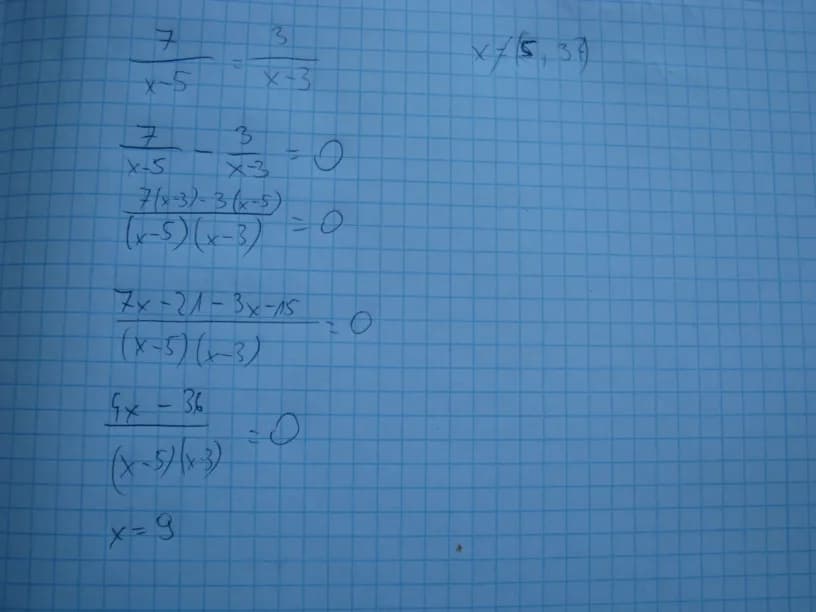Równania wymierne to istotny element matematyki, który pojawia się w różnych dziedzinach, od nauk ścisłych po codzienne życie. Aby skutecznie rozwiązać równanie wymierne, należy postępować według określonych kroków, które ułatwiają zrozumienie tego procesu. W tym artykule przedstawimy sprawdzone metody, które pozwolą Ci na efektywne rozwiązywanie równań wymiernych oraz uniknięcie najczęstszych błędów.
Rozpoczynając przygodę z równaniami wymiernymi, warto znać kilka kluczowych zasad, które pomogą w ich rozwiązaniu. Dzięki jasnym i prostym wskazówkom, każdy, niezależnie od poziomu zaawansowania, będzie mógł z powodzeniem poradzić sobie z tym matematycznym wyzwaniem.
Kluczowe wnioski:
- Równania wymierne można rozpoznać po obecności zmiennych w liczniku i mianowniku.
- Uproszczenie równania przed rozwiązaniem jest kluczowe dla uniknięcia błędów.
- Mnożenie przez wspólny mianownik pomaga w eliminacji ułamków, co ułatwia obliczenia.
- Unikanie dzielenia przez zero jest niezbędne, aby nie napotkać fałszywych rozwiązań.
- Praktyka na konkretnych przykładach pozwala na lepsze zrozumienie metod rozwiązywania równań wymiernych.
Jak zrozumieć podstawy równań wymiernych i ich rozwiązania
Równania wymierne to takie, w których zmienne występują zarówno w liczniku, jak i w mianowniku. W praktyce oznacza to, że równania te mają postać, w której możemy zobaczyć ułamki. Kluczowe jest, aby zrozumieć, że aby skutecznie je rozwiązać, musimy najpierw poznać ich definicję oraz cechy charakterystyczne. Równania wymierne można spotkać w różnych dziedzinach matematyki, a ich zrozumienie jest niezbędne do dalszej nauki i zastosowań.
Identyfikacja równań wymiernych jest kluczowa dla ich późniejszego rozwiązania. Aby je rozpoznać, można zwrócić uwagę na obecność zmiennych w mianowniku. Na przykład, równanie takie jak (2x + 3)/(x - 1) = 5 jest równaniem wymiernym, ponieważ zmienna x znajduje się w mianowniku. Warto również zauważyć, że równania wymierne mogą mieć różne formy, które mogą obejmować zarówno pojedyncze ułamki, jak i bardziej złożone struktury. Przykłady to (x + 2)/(x - 3) + 1 = 0 oraz (3x)/(x^2 - 1) = 2, które pokazują różnorodność równań wymiernych.
Co to są równania wymierne i jak je rozpoznać?
Równania wymierne to matematyczne wyrażenia, w których zmienne są umieszczone w ułamkach. Ich główną cechą jest to, że zarówno licznik, jak i mianownik mogą zawierać zmienne. Zrozumienie tej definicji jest kluczowe dla dalszego rozwiązywania takich równań. W praktyce, aby rozpoznać równanie wymierne, wystarczy zidentyfikować obecność zmiennych w mianowniku, co odróżnia je od równań liniowych czy kwadratowych.
- Równanie wymierne zawiera zmienne w liczniku i mianowniku.
- Przykłady równań wymiernych to (2x + 3)/(x - 1) = 5 oraz (x + 2)/(x - 3) + 1 = 0.
- Identyfikacja zmiennych w mianowniku jest kluczowa dla rozpoznania równań wymiernych.
Kluczowe zasady dotyczące rozwiązywania równań wymiernych
Rozwiązywanie równań wymiernych wymaga znajomości kilku kluczowych zasad, które są niezbędne do osiągnięcia poprawnych wyników. Jedną z najważniejszych zasad jest zrozumienie roli wspólnych mianowników. Umożliwiają one uproszczenie równań, co jest kluczowe w procesie ich rozwiązywania. Dodatkowo, ważne jest, aby unikać dzielenia przez zero, ponieważ prowadzi to do błędnych wyników. Każdy, kto chce skutecznie rozwiązywać równania wymierne, powinien również nauczyć się, jak identyfikować i eliminować fałszywe rozwiązania.
- Wspólny mianownik jest kluczowy dla uproszczenia równań wymiernych i pozwala na łatwiejsze obliczenia.
- Unikaj dzielenia przez zero, aby nie napotkać błędów w obliczeniach.
- Sprawdzaj rozwiązania, aby upewnić się, że nie są one fałszywe lub niepoprawne.
- Uproszczenie równań przed rozwiązaniem znacząco zwiększa szanse na uzyskanie prawidłowego wyniku.
- Stosowanie krok po kroku podejścia ułatwia proces rozwiązywania i pozwala na lepsze zrozumienie metod.
Skuteczne metody rozwiązywania równań wymiernych krok po kroku
Aby skutecznie rozwiązywać równania wymierne, warto stosować metody krok po kroku. Pierwszym krokiem jest zawsze uproszczenie równania, co może obejmować znalezienie wspólnego mianownika. Umożliwia to eliminację ułamków, co z kolei upraszcza dalsze obliczenia. Po uproszczeniu równania, można przejść do przenoszenia składników, co pozwala na łatwiejsze rozwiązanie dla niewiadomej. Kluczowe jest, aby każdy krok był dokładnie przemyślany i zapisany, aby uniknąć pomyłek.
Następnie, po przeniesieniu wszystkich składników na jedną stronę równania, można zacząć stosować różne techniki, takie jak mnożenie przez wspólny mianownik, aby uprościć równanie do postaci, która jest łatwiejsza do rozwiązania. Warto także pamiętać o sprawdzeniu uzyskanych rozwiązań, aby upewnić się, że są one poprawne i nie prowadzą do dzielenia przez zero. Dzięki tym metodom, każdy może nauczyć się, jak rozwiązywać równania wymierne skutecznie i bezbłędnie.
Jak uprościć równania wymierne przed rozwiązaniem?
Aby skutecznie rozwiązać równania wymierne, kluczowym krokiem jest ich upraszczanie przed przystąpieniem do obliczeń. Uproszczenie polega na redukcji skomplikowanych wyrażeń do prostszej formy, co ułatwia dalsze działania. Można to osiągnąć poprzez eliminację wspólnych czynników w liczniku i mianowniku, co pozwala na uproszczenie ułamków. Ponadto, warto zidentyfikować i wyeliminować wszelkie zbędne składniki, które nie wpływają na wynik równania. Dzięki tym technikom, proces rozwiązywania staje się znacznie bardziej przejrzysty i efektywny.
Techniki mnożenia przez wspólny mianownik dla uproszczenia
Mnożenie przez wspólny mianownik (LCD) to technika, która pozwala na eliminację ułamków w równaniach wymiernych. W praktyce polega to na pomnożeniu obu stron równania przez najmniejszy wspólny mianownik, co upraszcza równanie i umożliwia łatwiejsze obliczenia. Dzięki tej metodzie, wszystkie ułamki stają się całkowitymi liczbami, co znacząco ułatwia dalsze kroki w rozwiązywaniu. Warto pamiętać, że przed zastosowaniem tej techniki, należy upewnić się, że wspólny mianownik jest poprawnie obliczony, aby uniknąć błędów. Poniższa tabela przedstawia porównanie różnych mianowników i ich najmniejszych wspólnych mianowników.
| Mianownik | Najmniejszy wspólny mianownik (LCD) |
| x + 1, x - 2 | (x + 1)(x - 2) |
| 2, 3 | 6 |
| x, x + 3 | x(x + 3) |
Najczęstsze pułapki przy rozwiązywaniu równań wymiernych i jak ich unikać
Podczas rozwiązywania równań wymiernych można napotkać wiele pułapek, które mogą prowadzić do błędnych wyników. Jednym z najczęstszych błędów jest dzielenie przez zero, co nie tylko jest matematycznie niepoprawne, ale także prowadzi do nieokreślonych wyników. Inne powszechne błędy obejmują niewłaściwe upraszczanie równań oraz pomijanie istotnych składników. Aby uniknąć tych pułapek, ważne jest, aby dokładnie analizować każde równanie i stosować zasady matematyczne z należytą starannością. Systematyczne sprawdzanie każdego kroku w procesie rozwiązywania również może pomóc w wychwyceniu potencjalnych błędów.
Warto również zwrócić uwagę na fałszywe rozwiązania, które mogą pojawić się w wyniku niewłaściwego rozwiązywania równań wymiernych. Często zdarza się, że rozwiązania, które wydają się poprawne, w rzeczywistości nie spełniają warunków równania. Aby temu zapobiec, zawsze należy zweryfikować zdobyte wyniki, podstawiając je z powrotem do oryginalnego równania. Regularne stosowanie tych strategii pozwoli na zminimalizowanie błędów i zwiększenie skuteczności w rozwiązywaniu równań wymiernych.
Jak unikać błędów w mnożeniu i dzieleniu przez zera?
Unikanie błędów w mnożeniu i dzieleniu przez zero jest kluczowe w procesie rozwiązywania równań wymiernych. Dzielenie przez zero prowadzi do sytuacji, w której równanie staje się nieokreślone, co może zniekształcić wyniki obliczeń. Dlatego przed przystąpieniem do dzielenia, zawsze należy upewnić się, że mianownik nie przyjmuje wartości zerowej. W przypadku, gdy zmienna w mianowniku może stać się zerem, warto wcześniej określić jej dopuszczalne wartości, aby uniknąć takich sytuacji. Świadomość tych zasad jest kluczowa dla poprawnego rozwiązywania równań wymiernych.
Rozpoznawanie i eliminowanie fałszywych rozwiązań
Podczas rozwiązywania równań wymiernych ważne jest, aby zidentyfikować i wyeliminować fałszywe rozwiązania, które mogą pojawić się w wyniku niewłaściwego przekształcenia równań. Fałszywe rozwiązania to te, które wydają się być poprawne, ale nie spełniają oryginalnego równania. Aby sprawdzić, czy uzyskane rozwiązanie jest prawidłowe, należy je podstawić z powrotem do pierwotnego równania i upewnić się, że obie strony równania są równe. Jeśli wynik nie zgadza się, oznacza to, że rozwiązanie jest fałszywe i należy je odrzucić. Regularne sprawdzanie rozwiązań to kluczowy krok, który pomaga uniknąć błędów i zapewnia, że końcowe wyniki są wiarygodne.
Przykłady równań wymiernych z rozwiązaniami dla lepszego zrozumienia
Rozważmy przykład równania wymiernego: (x + 2)/(x - 3) = 4. Aby rozwiązać to równanie, zaczynamy od pomnożenia obu stron przez (x - 3), aby pozbyć się ułamka. Otrzymujemy: x + 2 = 4(x - 3). Następnie rozwijamy prawą stronę równania, co daje nam x + 2 = 4x - 12. Przenosimy x na jedną stronę i 12 na drugą, co prowadzi nas do 2 + 12 = 4x - x, a po uproszczeniu 14 = 3x, co daje x = 14/3.
Warto również sprawdzić uzyskane rozwiązanie. Podstawiając x = 14/3 z powrotem do oryginalnego równania, otrzymujemy: (14/3 + 2)/(14/3 - 3). Po przeliczeniu wartości w liczniku i mianowniku, upewniamy się, że wynik równania zgadza się z wcześniejszym obliczeniem. Dzięki temu mamy pewność, że rozwiązanie jest poprawne. Przykład ten pokazuje, jak ważne jest nie tylko uzyskanie rozwiązania, ale również jego weryfikacja w celu uniknięcia fałszywych wyników.
Jak wykorzystać równania wymierne w codziennym życiu i nauce
Równania wymierne mają zastosowanie nie tylko w matematyce, ale również w wielu dziedzinach życia codziennego oraz nauki. Przykładowo, w ekonomii można je wykorzystać do analizy kosztów i przychodów, pomagając w podejmowaniu decyzji dotyczących inwestycji. Zrozumienie, jak obliczać różne proporcje i ułamki, umożliwia lepsze zarządzanie finansami osobistymi oraz planowanie budżetu. W nauce, równania wymierne są często stosowane w chemii do obliczeń związanych z reakcjami chemicznymi, gdzie precyzyjne proporcje składników są kluczowe dla uzyskania pożądanych wyników.
Co więcej, w dobie rosnącej popularności technologii informacyjnych, umiejętność rozwiązywania równań wymiernych staje się coraz bardziej cenna. W programowaniu, na przykład, algorytmy często opierają się na matematyce, w tym na równaniach wymiernych, w celu optymalizacji procesów obliczeniowych. Zrozumienie tych równań może zatem otworzyć drzwi do kariery w dziedzinach związanych z analizą danych czy sztuczną inteligencją, gdzie matematyka odgrywa kluczową rolę w tworzeniu efektywnych modeli i rozwiązań.
