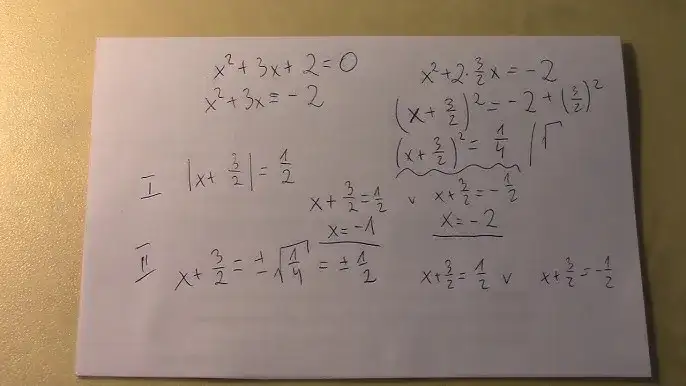Jak rozwiązać równanie kwadratowe? Kompletny przewodnik krok po kroku

Rozwiązywanie równań kwadratowych to jedna z podstawowych umiejętności, którą każdy uczeń szkoły średniej powinien opanować. Nie tylko stanowi kluczowy element programu nauczania matematyki, ale także jest nieocenionym narzędziem w wielu bardziej zaawansowanych zagadnieniach, a jej znajomość jest niezbędna podczas egzaminów maturalnych. W tym przewodniku przeprowadzimy Cię krok po kroku przez cały proces, od identyfikacji współczynników po interpretację wyników, dzięki czemu poczujesz się pewnie w każdym zadaniu tego typu.

Równanie kwadratowe bez tajemnic: dlaczego warto je opanować?

Czym jest równanie kwadratowe i gdzie je spotkasz?

Równanie kwadratowe to równanie wielomianowe drugiego stopnia. Jego ogólna postać, z którą najczęściej będziesz mieć do czynienia, to ax² + bx + c = 0. W tym wzorze litery a, b i c to współczynniki liczbowe, przy czym kluczowe jest to, że a nie może być równe zero (a ≠ 0). Gdyby a było zerem, równanie straciłoby człon z x² i stałoby się równaniem liniowym. Umiejętność rozwiązywania równań kwadratowych jest absolutnie fundamentalna w matematyce na poziomie szkoły średniej. Pojawia się ona nie tylko jako samodzielny temat, ale jest też nieodłącznym elementem zagadnień z geometrii analitycznej (np. przy znajdowaniu punktów przecięcia prostej z parabolą), optymalizacji czy analizy funkcji. Opanowanie tego tematu to pewny krok do sukcesu na maturze.

Krótka historia delty: dlaczego to najważniejsze narzędzie?

Kluczowym narzędziem, które pozwala nam szybko określić, ile rozwiązań ma dane równanie kwadratowe, jest tzw. wyróżnik trójmianu kwadratowego, powszechnie znany jako delta (Δ). To właśnie znak delty mówi nam, czy istnieją rozwiązania rzeczywiste, jedno rozwiązanie, czy może żadnego w zbiorze liczb rzeczywistych. Bez niej rozwiązywanie równań kwadratowych byłoby znacznie bardziej skomplikowane i czasochłonne.

Krok 1: Przygotowanie do bitwy jak poprawnie zidentyfikować współczynniki a, b, c?

Postać ogólna równania (ax² + bx + c = 0) Twój punkt wyjścia

Zanim przystąpimy do jakichkolwiek obliczeń, musimy dokładnie przyjrzeć się naszemu równaniu i zidentyfikować trzy kluczowe liczby: współczynniki a, b i c. Przypomnijmy sobie ogólną postać: ax² + bx + c = 0. Współczynnik a to liczba stojąca przy x², b to liczba stojąca przy x, a c to wyraz wolny (liczba bez x). Pamiętaj a musi być różne od zera, inaczej nie mamy do czynienia z równaniem kwadratowym.

Najczęstsze pułapki: uważaj na znaki i brakujące elementy!

Najwięcej błędów przy identyfikacji współczynników wynika z nieuwagi. Po pierwsze, zawsze zwracaj uwagę na znaki! Jeśli równanie wygląda tak: x² - 3x + 2 = 0, to a = 1 (bo przy x² jest niewidzialna jedynka), b = -3 (nie 3!) i c = 2. Po drugie, uważaj na równania niepełne, gdzie brakuje któregoś ze współczynników. Jeśli równanie to x² - 9 = 0, to a = 1, b = 0 (bo nie ma wyrazu z samym x), a c = -9. Jeśli równanie to 2x² + 5x = 0, to a = 2, b = 5, a c = 0.

Praktyczne przykłady: rozpoznawanie współczynników w różnych równaniach

• Równanie: x² + 5x + 6 = 0
  Współczynniki: a = 1, b = 5, c = 6
• Równanie: -x² + 2x - 1 = 0
  Współczynniki: a = -1, b = 2, c = -1
• Równanie: 3x² - 12 = 0 (równanie niepełne, b=0)
  Współczynniki: a = 3, b = 0, c = -12
• Równanie: x² + 4x = 0 (równanie niepełne, c=0)
  Współczynniki: a = 1, b = 4, c = 0
• Równanie: -2x² - x + 7 = 0
  Współczynniki: a = -2, b = -1, c = 7

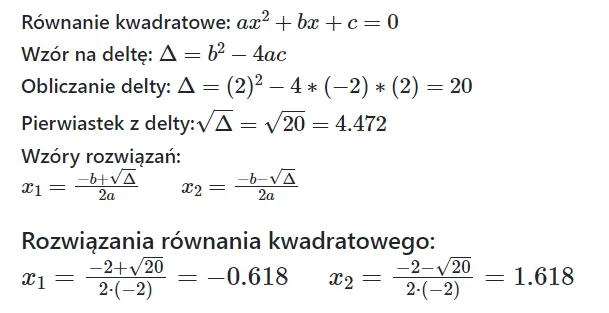
Krok 2: Serce operacji liczymy deltę (Δ) krok po kroku

Wzór, który musisz znać na pamięć: Δ = b² - 4ac

Teraz, gdy już bezbłędnie identyfikujemy współczynniki, możemy przejść do serca całego procesu obliczenia delty. Wzór jest prosty, ale wymaga precyzji: Δ = b² - 4ac. Pamiętaj, że b² oznacza b pomnożone przez siebie (b * b), a -4ac to iloczyn liczb -4, a oraz c.

Jak podstawiać wartości, by uniknąć błędów rachunkowych?

• Zawsze używaj nawiasów przy podstawianiu liczb ujemnych! To najczęstsze źródło błędów. Na przykład, jeśli b = -3, to b² = (-3)² = 9, a nie -9.
• Uważaj na kolejność działań. Najpierw wykonaj potęgowanie (b²), potem mnożenie (4ac), a na końcu odejmowanie.
• Podwójnie sprawdź znaki w całym wyrażeniu -4ac. Jeśli a i c mają różne znaki, -4ac będzie dodatnie. Jeśli mają takie same znaki, -4ac będzie ujemne.

Obliczanie delty na konkretnych przykładach przećwicz to z nami

1. Równanie: x² + 5x + 6 = 0 (a=1, b=5, c=6)
   Δ = b² - 4ac = (5)² - 4 * 1 * 6 = 25 - 24 = 1
2. Równanie: x² - 6x + 9 = 0 (a=1, b=-6, c=9)
   Δ = b² - 4ac = (-6)² - 4 * 1 * 9 = 36 - 36 = 0
3. Równanie: x² + 2x + 5 = 0 (a=1, b=2, c=5)
   Δ = b² - 4ac = (2)² - 4 * 1 * 5 = 4 - 20 = -16

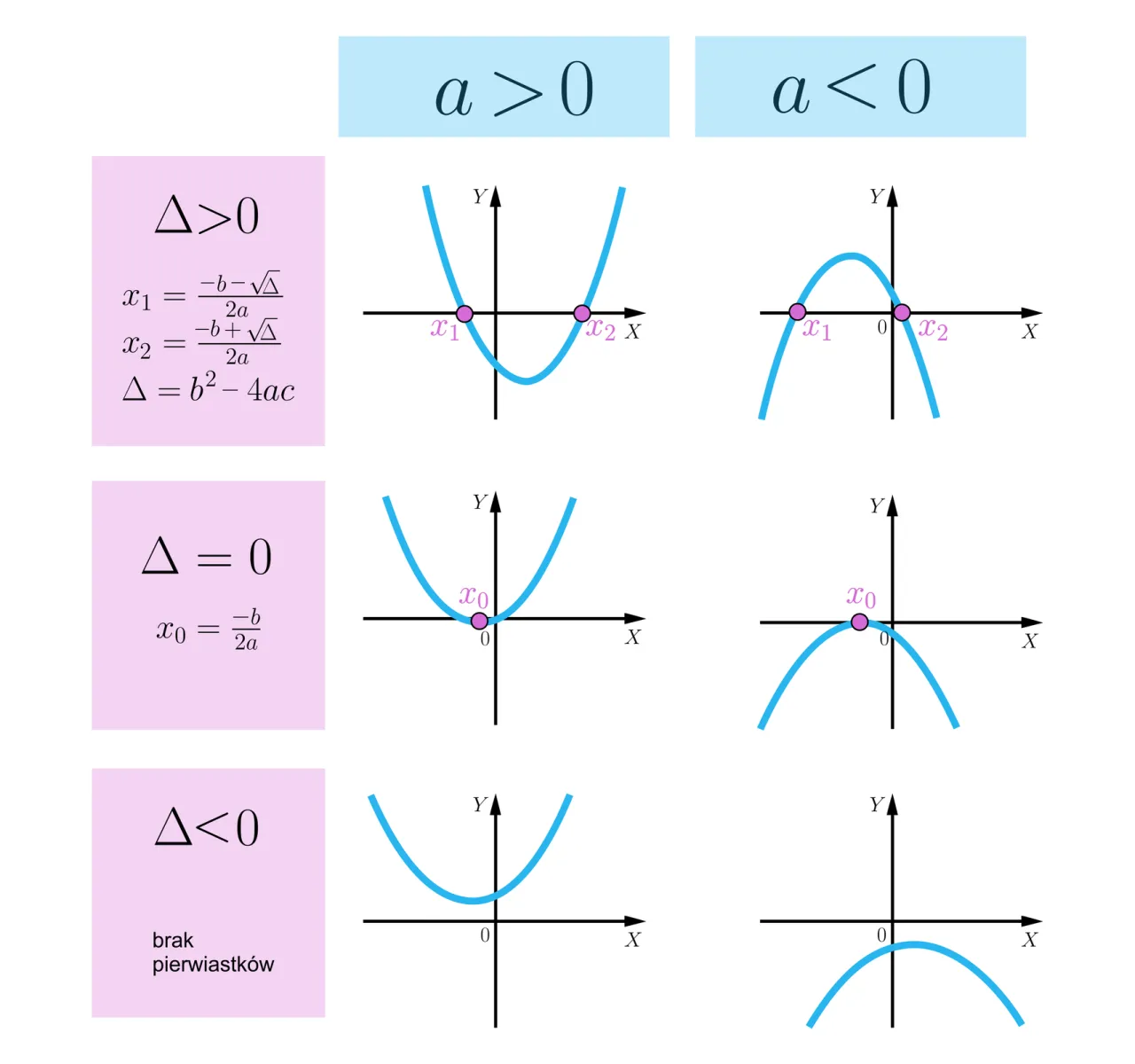
Krok 3: Interpretacja wyników co tak naprawdę mówi Ci znak delty?

Przypadek 1: Delta większa od zera (Δ > 0) dwa rozwiązania na horyzoncie

Gdy obliczona delta jest liczbą dodatnią (Δ > 0), oznacza to, że nasze równanie kwadratowe ma dwa różne pierwiastki rzeczywiste. To dobra wiadomość, bo mamy konkretne wzory, które pozwolą nam je wyznaczyć.

Jak obliczyć pierwiastki x₁ i x₂ używając wzorów?

Wzory na dwa pierwiastki rzeczywiste, gdy Δ > 0, są następujące:
x₁ = (-b - √Δ) / 2a
x₂ = (-b + √Δ) / 2a
Wystarczy podstawić wartości współczynników a, b oraz obliczoną deltę (a konkretnie jej pierwiastek kwadratowy) do tych wzorów, aby otrzymać oba rozwiązania.

Przykładowe równanie z dwoma rozwiązaniami zobacz, jakie to proste

1. Rozważmy równanie: x² + 5x + 6 = 0.
2. Zidentyfikowaliśmy współczynniki: a = 1, b = 5, c = 6.
3. Obliczyliśmy deltę: Δ = 1.
4. Ponieważ Δ > 0, obliczamy dwa pierwiastki:
   • √Δ = √1 = 1
   • x₁ = (-5 - 1) / (2 * 1) = -6 / 2 = -3
   • x₂ = (-5 + 1) / (2 * 1) = -4 / 2 = -2
5. Rozwiązaniami równania są liczby x = -3 oraz x = -2.

Przypadek 2: Delta równa zero (Δ = 0) jedno, ale za to podwójne rozwiązanie

Jeśli po obliczeniach okaże się, że delta jest równa zero (Δ = 0), oznacza to, że równanie kwadratowe ma tylko jedno rozwiązanie rzeczywiste. Jest ono nazywane pierwiastkiem podwójnym, ponieważ można je traktować jako dwa takie same pierwiastki.

Wzór na jedyny pierwiastek x₀ dlaczego jest prostszy?

Gdy Δ = 0, wzór na pierwiastek znacznie się upraszcza, ponieważ pierwiastek z zera to zero. Wzór wygląda tak:
x₀ = -b / 2a
Jak widać, nie musimy już dodawać ani odejmować pierwiastka z delty, co czyni obliczenia szybszymi.

Przykład równania z jednym rozwiązaniem opanuj tę sytuację

1. Rozważmy równanie: x² - 6x + 9 = 0.
2. Zidentyfikowaliśmy współczynniki: a = 1, b = -6, c = 9.
3. Obliczyliśmy deltę: Δ = 0.
4. Ponieważ Δ = 0, obliczamy jeden pierwiastek:
   • x₀ = -(-6) / (2 * 1) = 6 / 2 = 3
5. Rozwiązaniem równania jest liczba x = 3 (jest to pierwiastek podwójny).

Przypadek 3: Delta mniejsza od zera (Δ < 0) czy to koniec zadania?

Kiedy delta jest liczbą ujemną (Δ < 0), oznacza to, że nasze równanie nie ma rozwiązań w zbiorze liczb rzeczywistych. W kontekście typowej nauki w szkole średniej zazwyczaj na tym kończymy analizę tego przypadku.

Dlaczego mówimy "brak rozwiązań w zbiorze liczb rzeczywistych"?

Powodem, dla którego nie możemy znaleźć rozwiązań, jest fakt, że w zbiorze liczb rzeczywistych nie istnieje pierwiastek kwadratowy z liczby ujemnej. Wzory na pierwiastki wymagają obliczenia √Δ, a jeśli Δ jest ujemne, napotykamy na matematyczną niemożliwość w ramach liczb rzeczywistych. (W bardziej zaawansowanej matematyce istnieją liczby zespolone, które pozwalają na takie obliczenia, ale to już inna historia).

Przykład równania bez rozwiązań kiedy możesz odłożyć długopis?

1. Rozważmy równanie: x² + 2x + 5 = 0.
2. Zidentyfikowaliśmy współczynniki: a = 1, b = 2, c = 5.
3. Obliczyliśmy deltę: Δ = -16.
4. Ponieważ Δ < 0, stwierdzamy, że równanie nie ma rozwiązań w zbiorze liczb rzeczywistych. Możemy zakończyć zadanie.

A co, jeśli można prościej? Metody alternatywne dla sprytnych

Równania niepełne: gdy b = 0 lub c = 0 zapomnij o delcie!

W przypadku równań niepełnych, czyli takich, gdzie brakuje wyrazu z x (b=0) lub wyrazu wolnego (c=0), często można rozwiązać je znacznie szybciej, bez uciekania się do liczenia delty.
Gdy b = 0 (postać ax² + c = 0): Przekształcamy równanie do postaci ax² = -c, a następnie x² = -c/a. Jeśli -c/a jest liczbą nieujemną, istnieją dwa rozwiązania: x = √(-c/a) oraz x = -√(-c/a). Jeśli -c/a jest ujemne, brak rozwiązań rzeczywistych.
Przykład: 2x² - 8 = 0 => 2x² = 8 => x² = 4 => x = 2 lub x = -2.
Gdy c = 0 (postać ax² + bx = 0): Wyciągamy x przed nawias: x(ax + b) = 0. Iloczyn jest równy zero, gdy jeden z czynników jest równy zero. Zatem x = 0 lub ax + b = 0. Drugie równanie daje nam x = -b/a.
Przykład: 3x² + 6x = 0 => x(3x + 6) = 0 => x = 0 lub 3x + 6 = 0 => 3x = -6 => x = -2. Rozwiązania to x = 0 i x = -2.

Wzory Viète’a: jak mogą pomóc w sprawdzeniu wyniku?

Wzory Viète’a to elegancki sposób na powiązanie pierwiastków równania kwadratowego z jego współczynnikami. Choć nie służą one bezpośrednio do znajdowania pierwiastków, są nieocenione przy sprawdzaniu poprawności obliczeń lub w rozwiązywaniu bardziej złożonych zadań. Wzory te wyglądają następująco:
x₁ + x₂ = -b/a (suma pierwiastków)
x₁ * x₂ = c/a (iloczyn pierwiastków)
Jeśli obliczyłeś pierwiastki x₁ i x₂, możesz szybko sprawdzić, czy ich suma jest równa -b/a, a ich iloczyn jest równy c/a. Jeśli tak, Twoje rozwiązanie jest prawdopodobnie poprawne.

Najczęstsze błędy uczniów sprawdź, czy ich nie popełniasz!

Pomyłki w znakach przy współczynnikach wróg numer jeden

To absolutnie kluczowa kwestia. Wielokrotnie podkreślamy, jak ważne jest dokładne odczytywanie znaków współczynników a, b i c. Nawet jeden źle przepisany minus może sprawić, że całe obliczenia pójdą na marne. Zawsze zapisuj równanie w postaci ax² + bx + c = 0 i dokładnie przypisuj wartości, zwracając szczególną uwagę na znaki, zwłaszcza gdy są one ujemne.

Błędne potęgowanie i kolejność działań przy liczeniu delty

Kolejnym częstym problemem są błędy rachunkowe przy obliczaniu delty. Pamiętaj, że (-b)² to nie to samo co -b². Na przykład, jeśli b = -4, to b² = (-4)² = 16, podczas gdy -b² = -(-4)² = -16. Zawsze używaj nawiasów przy podstawianiu ujemnych wartości. Uważaj też na kolejność działań: potęgowanie, mnożenie, a na końcu odejmowanie.

Problemy z pierwiastkowaniem delty jak sobie z tym radzić?

Czasem zdarza się, że delta nie jest idealnym kwadratem liczby całkowitej (np. Δ = 7). W takiej sytuacji, jeśli zadanie nie wymaga podania przybliżonej wartości, najlepszym rozwiązaniem jest pozostawienie pierwiastka w postaci √Δ. Na przykład, jeśli Δ = 7, pierwiastki to x₁ = (-b - √7) / 2a i x₂ = (-b + √7) / 2a. Próba obliczenia przybliżonej wartości √7 bez kalkulatora może prowadzić do błędów.

Twoja ściągawka: cały proces rozwiązywania w 5 krokach

1. Zidentyfikuj współczynniki: Zapisz równanie w postaci ax² + bx + c = 0 i dokładnie odczytaj wartości a, b, c, zwracając uwagę na znaki.
2. Oblicz deltę: Użyj wzoru Δ = b² - 4ac, podstawiając wartości współczynników. Pamiętaj o nawiasach dla liczb ujemnych i kolejności działań.
3. Zinterpretuj znak delty:
   • Jeśli Δ > 0: Są dwa rozwiązania rzeczywiste.
   • Jeśli Δ = 0: Jest jedno rozwiązanie rzeczywiste (podwójne).
   • Jeśli Δ < 0: Brak rozwiązań rzeczywistych.
4. Oblicz pierwiastki (jeśli istnieją):
   • Dla Δ > 0: Użyj wzorów x₁ = (-b - √Δ) / 2a i x₂ = (-b + √Δ) / 2a.
   • Dla Δ = 0: Użyj wzoru x₀ = -b / 2a.
5. Sprawdź (opcjonalnie): Użyj wzorów Viète’a (x₁ + x₂ = -b/a, x₁ * x₂ = c/a), aby upewnić się, że Twoje obliczenia są poprawne.

Przeczytaj również: Rozwiąż równanie i sprawdź, czy spełnia je liczba naturalna

Twoja ścieżka do mistrzostwa w równaniach kwadratowych co dalej?

Gratulacje! Przeszliśmy przez wszystkie kluczowe etapy rozwiązywania równań kwadratowych od identyfikacji współczynników, przez obliczanie i interpretację delty, aż po wyznaczanie pierwiastków i poznanie metod alternatywnych. Teraz wiesz, jak krok po kroku poradzić sobie z każdym równaniem kwadratowym, a także jak unikać najczęstszych pułapek.

Kluczowe wnioski, które warto zapamiętać:

• Precyzyjne określenie współczynników a, b, c jest absolutną podstawą.
• Delta (Δ) jest Twoim kompasem jej znak decyduje o liczbie rozwiązań.
• Nie zapominaj o nawiasach i kolejności działań przy obliczaniu delty, zwłaszcza z liczbami ujemnymi.
• Równania niepełne często można rozwiązać prościej, pomijając deltę.

Z mojego doświadczenia wynika, że najwięcej trudności sprawia początkowe oswojenie się z samą ideą delty i jej interpretacją. Jednak po kilku samodzielnie rozwiązanych przykładach, wszystko staje się znacznie jaśniejsze. Pamiętaj, że praktyka czyni mistrza im więcej równań rozwiążesz, tym pewniej będziesz się czuć. Nie zniechęcaj się pierwszymi potknięciami, bo każdy błąd to cenna lekcja.

Jakie są Twoje największe wyzwania podczas rozwiązywania równań kwadratowych? Czy któraś z metod okazała się dla Ciebie szczególnie pomocna? Podziel się swoimi przemyśleniami w komentarzach!