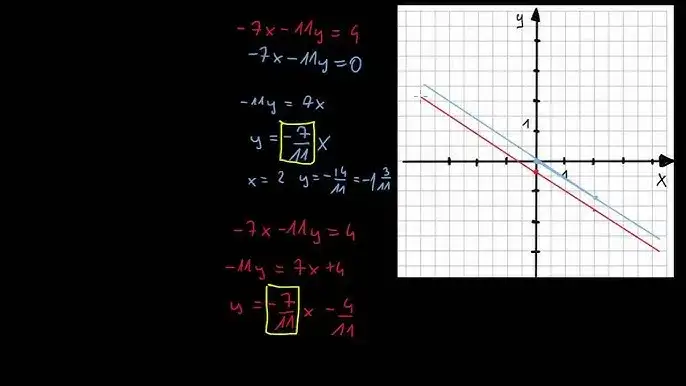
Wskazanie równoważnego układu równań jest kluczowym zagadnieniem w matematyce, które pozwala na zrozumienie, czy dwa układy równań mają ten sam zbiór rozwiązań. Dwa układy są równoważne, gdy ich rozwiązania są identyczne, co ma ogromne znaczenie w rozwiązywaniu problemów matematycznych. W praktyce oznacza to, że jeśli potrafimy znaleźć rozwiązanie jednego układu, możemy je wykorzystać do analizy drugiego układu.
W artykule omówimy, jak zdefiniować równoważne układy równań oraz jakie metody można zastosować do ich identyfikacji. Przedstawimy również praktyczne przykłady oraz najczęstsze błędy, które mogą wystąpić podczas obliczeń. Dzięki temu, czytelnik zyska nie tylko teoretyczną wiedzę, ale także praktyczne umiejętności, które pomogą mu uniknąć pułapek w obliczeniach.
Najważniejsze informacje:
- Równoważne układy równań mają ten sam zbiór rozwiązań.
- Aby sprawdzić równoważność, wystarczy podstawić rozwiązania do drugiego układu.
- Techniki przekształcania układów równań, takie jak podstawianie i eliminacja, są kluczowe dla identyfikacji równoważności.
- Przykłady prostych i złożonych układów równań pomagają lepiej zrozumieć temat.
- Unikanie typowych błędów w obliczeniach jest niezbędne do prawidłowego rozwiązywania układów równań.
Jak zdefiniować równoważne układy równań i ich znaczenie
Równoważne układy równań to takie, które mają ten sam zbiór rozwiązań. W matematyce zrozumienie tej koncepcji jest kluczowe, ponieważ pozwala na uproszczenie problemów oraz efektywne stosowanie różnych metod rozwiązywania. Dzięki identyfikacji równoważnych układów, można łatwiej porównywać różne podejścia do tego samego problemu. W praktyce oznacza to, że jeśli potrafimy znaleźć rozwiązanie jednego układu, możemy je zastosować do innego, równoważnego układu, co oszczędza czas i wysiłek.
Równoważność układów równań ma również zastosowanie w wielu dziedzinach matematyki i nauk ścisłych. Umożliwia to nie tylko rozwiązywanie problemów teoretycznych, ale także praktyczne zastosowanie w inżynierii, ekonomii czy przy modelowaniu zjawisk naturalnych. Właściwe zrozumienie tej koncepcji jest fundamentem dla dalszej nauki i stosowania bardziej zaawansowanych technik matematycznych.
Równoważność układów równań – kluczowe pojęcia i definicje
Równoważność układów równań odnosi się do relacji między dwoma lub więcej układami, które mają identyczne rozwiązania. Termin "układ równań" odnosi się do zestawu równań, które należy rozwiązać jednocześnie. W kontekście układów liniowych, równoważność oznacza, że wszystkie rozwiązania jednego układu są również rozwiązaniami drugiego układu. Na przykład, układ równań z dwiema niewiadomymi jest równoważny, jeśli dla każdej pary wartości zmiennych spełnia równania obu układów.
Równoważność jest istotna, ponieważ pozwala na zrozumienie, jak różne układy mogą być przekształcane w siebie nawzajem bez utraty ich rozwiązań. Definiowanie równoważności układów równań jest kluczowe dla analizy matematycznej i umożliwia uczniom oraz profesjonalistom w łatwy sposób przekształcać i rozwiązywać skomplikowane problemy. Wiedza na temat równoważności układów równań jest niezbędna, aby skutecznie poruszać się w świecie matematyki i jej zastosowań.
Dlaczego znajomość równoważności jest istotna w matematyce
Znajomość równoważności układów równań jest kluczowa zarówno dla uczniów, jak i profesjonalistów w dziedzinie matematyki. Równoważność pozwala na uproszczenie problemów i zwiększa efektywność rozwiązywania równań. Dzięki zrozumieniu, które układy są równoważne, można stosować różne metody i techniki, aby uzyskać rozwiązania szybciej i łatwiej. Dodatkowo, umiejętność identyfikacji równoważnych układów równań jest niezbędna w sytuacjach, gdy potrzebne jest porównanie różnych modeli matematycznych.
Praktyczne zastosowania znajomości równoważności są szerokie. W inżynierii, ekonomii czy naukach przyrodniczych, umiejętność rozwiązywania równoważnych układów równań pozwala na lepsze modelowanie zjawisk i procesów. Właściwe zrozumienie tej koncepcji wpływa na zdolność do podejmowania świadomych decyzji oraz rozwiązywania złożonych problemów, co jest niezwykle cenne w różnych dziedzinach życia zawodowego. Dlatego inwestowanie czasu w naukę o równoważności układów równań przynosi długofalowe korzyści.
Metody identyfikacji równoważnych układów równań
Istnieje wiele metod, które można zastosować do identyfikacji równoważnych układów równań. Ważne jest, aby zrozumieć, że każda z tych metod ma swoje zastosowanie w różnych kontekstach matematycznych. W kolejnych sekcjach omówimy techniki takie jak podstawianie, eliminacja oraz przekształcanie układów równań, które pozwalają na ustalenie, czy dwa układy są równoważne. Poznanie tych metod jest niezbędne dla każdego, kto pragnie skutecznie rozwiązywać układy równań.Właściwe stosowanie tych technik umożliwia nie tylko efektywne rozwiązanie problemów, ale również lepsze zrozumienie struktury układów równań. Każda z metod ma swoje unikalne cechy, które mogą być przydatne w różnych sytuacjach. Dlatego warto eksperymentować z różnymi podejściami, aby znaleźć te, które najlepiej pasują do konkretnych problemów matematycznych.
Krok po kroku – jak sprawdzić równoważność układów równań
Aby sprawdzić, czy dwa układy równań są równoważne, należy postępować zgodnie z określonymi krokami. Po pierwsze, należy znaleźć rozwiązania jednego z układów. Następnie, te rozwiązania powinny być podstawione do drugiego układu, aby sprawdzić, czy spełniają wszystkie jego równania. Jeśli tak, to układy są równoważne. W przeciwnym razie, jeśli rozwiązanie nie pasuje do drugiego układu, układy nie są równoważne.
Ważne jest, aby dokładnie przeanalizować każdy krok, aby uniknąć błędów. Weryfikacja równoważności układów równań to proces, który wymaga staranności i precyzji. Przestrzeganie tych kroków pomoże w zrozumieniu relacji między różnymi układami równań oraz ich zastosowaniem w praktycznych problemach matematycznych.
- Znajdź rozwiązanie pierwszego układu równań.
- Podstaw to rozwiązanie do drugiego układu równań.
- Sprawdź, czy rozwiązanie spełnia wszystkie równania drugiego układu.
- Jeśli tak, układy są równoważne; jeśli nie, układy nie są równoważne.
Techniki przekształcania układów równań dla równoważności
Istnieje kilka technik, które można zastosować do przekształcania układów równań, aby sprawdzić ich równoważność. Jedną z najczęściej stosowanych metod jest podstawianie, które polega na wyznaczeniu jednej zmiennej w jednym równaniu i podstawieniu jej do drugiego równania. Inną popularną techniką jest eliminacja, gdzie dodajemy lub odejmujemy równania, aby wyeliminować jedną z niewiadomych. Obie metody są skuteczne i mogą być używane w różnych sytuacjach, w zależności od układu równań.
Techniki te pozwalają na uproszczenie układów równań, co ułatwia ich rozwiązanie. Ważne jest, aby unikać typowych błędów, takich jak nieprawidłowe przekształcenia czy błędne podstawienia, które mogą prowadzić do błędnych wyników. Zrozumienie, jak skutecznie stosować te techniki, jest kluczowe dla każdego, kto chce opanować umiejętność rozwiązywania układów równań.
Przykłady równoważnych układów równań w praktyce
Przykłady równoważnych układów równań są niezwykle ważne, ponieważ pomagają zrozumieć, jak różne układy mogą mieć identyczne rozwiązania. Analiza takich przykładów pozwala na praktyczne zastosowanie teorii w realnych sytuacjach, co jest kluczowe dla studentów i praktyków matematyki. W tej sekcji przedstawimy kilka prostych układów równań, które są równoważne, aby zobrazować tę koncepcję.
Analiza prostych układów równań i ich równoważność
Rozważmy dwa układy równań, które są równoważne. Pierwszy układ to:
$$ 2x + y = 5 \\ x - y = 1 $$
Rozwiązaniem tego układu jest para liczb $$x = 2$$, $$y = 1$$. Teraz rozważmy drugi układ równań:
$$ 3x + 2y = 8 \\ -2x + 4y = 0 $$
Ten układ również ma to samo rozwiązanie, $$x = 2$$ oraz $$y = 1$$. Obydwa układy są więc równoważne, ponieważ mają ten sam zbiór rozwiązań.
| Układ Równań | Rozwiązanie (x, y) |
| 2x + y = 5; x - y = 1 | (2, 1) |
| 3x + 2y = 8; -2x + 4y = 0 | (2, 1) |
Złożone układy równań – jak je porównywać i weryfikować
W przypadku bardziej złożonych układów równań, porównywanie i weryfikowanie ich równoważności staje się kluczowe dla prawidłowego rozwiązywania problemów matematycznych. Na przykład, rozważmy układy równań:
$$ 5 - 2x + 3y = 7 \\ 4x + y = 8 $$
oraz
$$ 2x - 3y = -1 \\ x + 2y = 5 $$
Aby określić, czy te układy są równoważne, musimy znaleźć ich rozwiązania i porównać je. Możemy to zrobić, stosując różne metody, takie jak podstawianie lub eliminacja, aby wyznaczyć wartości zmiennych i sprawdzić, czy są identyczne.
Weryfikacja równoważności układów równań polega na podstawieniu rozwiązania jednego układu do drugiego. Jeśli rozwiązania są zgodne, układy są równoważne. W przeciwnym razie, należy przeanalizować, dlaczego tak się stało i czy nie wystąpiły błędy w obliczeniach.

Jak unikać typowych błędów w obliczeniach układów równań
Unikanie typowych błędów jest kluczowe w pracy z układami równań. Wielu uczniów i profesjonalistów popełnia błędy podczas przekształcania równań lub podstawiania wartości, co prowadzi do błędnych wyników. Dlatego ważne jest, aby być świadomym najczęstszych pułapek, które mogą się pojawić w trakcie rozwiązywania układów równań.
Najczęstsze pułapki przy identyfikacji równoważnych układów
W pracy z układami równań, istnieje kilka typowych błędów, które mogą prowadzić do nieprawidłowych wyników. Nieprawidłowe przekształcenia równań mogą skutkować błędnymi rozwiązaniami, a także pominięcie kroków w procesie eliminacji lub podstawiania. Ważne jest, aby dokładnie sprawdzać każdy krok i upewnić się, że operacje są wykonywane poprawnie.
- Nieprawidłowe przekształcanie równań, które prowadzi do błędnych wyników.
- Pomijanie kroków w procesie eliminacji lub podstawiania.
- Brak weryfikacji rozwiązania w drugim układzie równań.
Jak wykorzystać równoważność układów równań w programowaniu
W dzisiejszym świecie technologii, umiejętność pracy z równoważnymi układami równań ma zastosowanie nie tylko w matematyce, ale również w programowaniu i analizie danych. Wiele algorytmów, zwłaszcza w obszarze uczenia maszynowego, opiera się na modelowaniu zjawisk za pomocą równań. Zrozumienie, jak identyfikować i przekształcać równania, pozwala programistom na tworzenie bardziej efektywnych modeli, które mogą lepiej przewidywać wyniki na podstawie danych wejściowych.W praktyce, programiści mogą wykorzystać równoważność układów równań do optymalizacji algorytmów, co prowadzi do szybszego przetwarzania danych i lepszej wydajności aplikacji. Na przykład, w analizie danych, równania mogą być przekształcane w celu uproszczenia obliczeń, co jest szczególnie ważne w przypadku dużych zbiorów danych. Dzięki znajomości tych technik, można nie tylko poprawić dokładność modeli, ale także zredukować czas potrzebny na ich obliczenia, co jest kluczowe w dynamicznie zmieniającym się środowisku technologicznym.