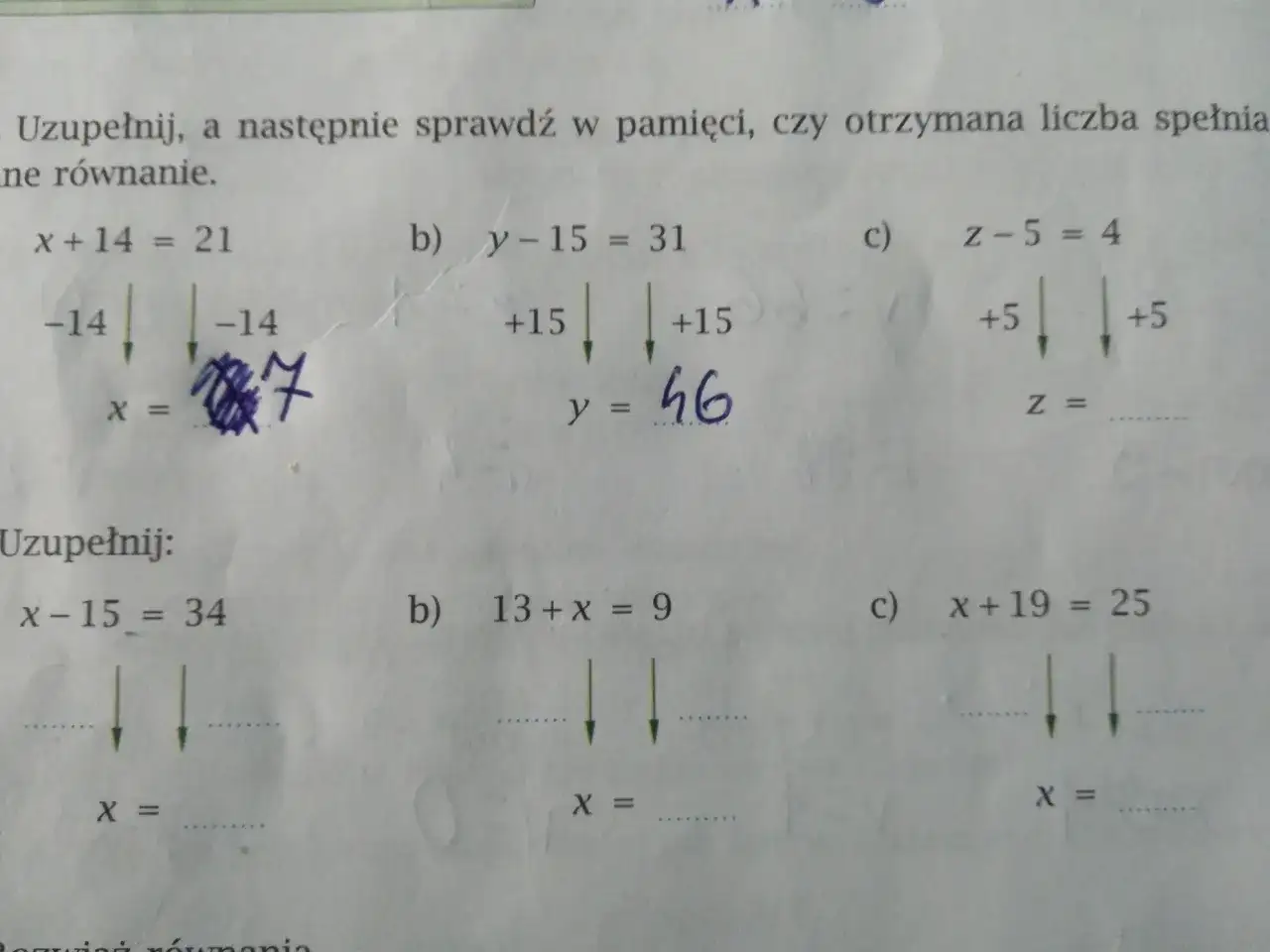Rozwiązywanie równań to kluczowa umiejętność w matematyce, a jednym z istotnych zagadnień jest określenie, czy uzyskane rozwiązania należą do zbioru liczb naturalnych. Liczby naturalne to te, które zaczynają się od zera i obejmują wszystkie liczby całkowite dodatnie. W artykule przyjrzymy się, jak rozwiązywać równania oraz jak sprawdzić, czy ich rozwiązania są liczbami naturalnymi. Zrozumienie tego procesu jest niezbędne, aby móc skutecznie pracować z równaniami w różnych kontekstach matematycznych.
W dalszej części artykułu zaprezentowane zostaną przykłady równań oraz metody ich rozwiązania, a także sposoby weryfikacji, czy uzyskane wyniki są liczbami naturalnymi. Dzięki temu będziesz mógł nie tylko rozwiązywać równania, ale również oceniać, które z nich spełniają warunki dotyczące liczb naturalnych.
Kluczowe informacje:
- Równania można rozwiązywać na różne sposoby, a każdy z nich może prowadzić do różnych typów rozwiązań.
- Sprawdzenie, czy rozwiązanie jest liczbą naturalną, wymaga znajomości definicji tego zbioru.
- W matematyce liczby naturalne są istotne w wielu zastosowaniach, w tym w zadaniach praktycznych.
- Analiza równań liniowych i kwadratowych wymaga różnych podejść, co zostanie szczegółowo omówione w artykule.
- Weryfikacja rozwiązania jako liczby naturalnej polega na ocenie, czy wynik mieści się w definicji zbioru liczb naturalnych.
Jak rozwiązać równanie i sprawdzić naturalne liczby jako rozwiązania
Rozwiązywanie równań to kluczowa umiejętność w matematyce, a także w codziennym życiu. Aby sprawdzić, czy rozwiązanie równania jest liczbą naturalną, musimy najpierw zrozumieć, jak rozwiązywać różne typy równań. Proces ten obejmuje przekształcanie równań w taki sposób, aby uzyskać wartość zmiennej, a następnie ocenę, czy ta wartość należy do zbioru liczb naturalnych, który obejmuje liczby całkowite dodatnie oraz zero.
Ważnym krokiem jest analiza uzyskanych rozwiązań. Po rozwiązaniu równania, należy zweryfikować, czy wynik spełnia warunki dla liczb naturalnych. W przypadku, gdy wynik jest liczbą ujemną lub ułamkiem, nie spełnia on kryteriów zbioru liczb naturalnych. W dalszej części artykułu przedstawimy konkretne przykłady równań oraz metody weryfikacji, które pomogą w zrozumieniu tego procesu.
Przykłady równań z naturalnymi rozwiązaniami i ich rozwiązanie
Rozważmy równanie: $$(x - 5)(x + 1) = x^2$$. Po rozwinięciu lewą stronę równania otrzymujemy:
$$x^2 + x - 5x - 5 = x^2$$, co upraszcza się do $$x^2 - 4x - 5 = x^2$$. Odejmując $$x^2$$ od obu stron, mamy $$-4x - 5 = 0$$, co prowadzi nas do $$x = -\frac{5}{4}$$. Ponieważ $$-\frac{5}{4}$$ nie jest liczbą naturalną, to to równanie nie spełnia naszego kryterium.
Kolejnym przykładem jest równanie: $$(1 + x)(2 - x) + x^2 = 3$$. Rozwijając lewą stronę, uzyskujemy $$2 + x = 3$$, co prowadzi do $$x = 1$$. Liczba $$1$$ jest liczbą naturalną, więc to równanie spełnia nasze wymagania. Te przykłady pokazują, jak ważne jest nie tylko rozwiązywanie równań, ale również sprawdzanie, czy wyniki są liczbami naturalnymi.
- Równanie liniowe: $$2x + 3 = 7$$, rozwiązanie: $$x = 2$$ (liczba naturalna).
- Równanie kwadratowe: $$x^2 - 4 = 0$$, rozwiązanie: $$x = 2$$ lub $$x = -2$$ (tylko $$2$$ jest liczbą naturalną).
- Równanie z ułamkiem: $$\frac{x}{2} = 3$$, rozwiązanie: $$x = 6$$ (liczba naturalna).
Jak zweryfikować, czy rozwiązanie jest liczbą naturalną
Aby zweryfikować, czy rozwiązanie równania jest liczbą naturalną, należy przede wszystkim zrozumieć definicję liczb naturalnych. Zbiór liczb naturalnych to liczby całkowite nieujemne, czyli $$\mathbb{N} = \{0, 1, 2, 3, \ldots\}$$. Po uzyskaniu rozwiązania równania, sprawdzamy, czy wynik jest liczbą całkowitą oraz czy jest większy lub równy zeru. Jeśli tak, to rozwiązanie spełnia warunki dla liczb naturalnych.Ważnym krokiem w weryfikacji jest także unikanie pułapek, takich jak mylenie liczb ujemnych lub ułamków z liczbami naturalnymi. Przykładowo, rozwiązanie $$x = -2$$ lub $$x = \frac{1}{2}$$ nie jest liczbą naturalną. Dlatego, zawsze należy upewnić się, że uzyskany wynik jest zgodny z definicją liczb naturalnych, aby móc stwierdzić, czy spełnia wymagania danego równania.
Zbiór liczb naturalnych: co go definiuje i jak go używać
Zbiór liczb naturalnych, oznaczany jako $$\mathbb{N}$$, obejmuje wszystkie liczby całkowite nieujemne, czyli $$\{0, 1, 2, 3, \ldots\}$$. Naturalne liczby są podstawą wielu działań matematycznych i są powszechnie stosowane w różnych kontekstach, takich jak liczenie, porządkowanie czy definiowanie zbiorów. W matematyce, liczby naturalne są wykorzystywane do rozwiązywania równań, gdzie często poszukujemy takich wartości, które spełniają określone warunki.
W praktyce, liczby naturalne znajdują zastosowanie w różnych dziedzinach, takich jak statystyka, ekonomia czy informatyka. Umożliwiają one łatwe modelowanie sytuacji, w których mówimy o ilościach całkowitych, jak liczba osób, przedmiotów czy zdarzeń. Dzięki swojej prostocie i intuicyjności, liczby naturalne są fundamentalnym elementem matematyki, który ułatwia zrozumienie bardziej złożonych koncepcji.
Różnice między liczbami naturalnymi a innymi zbiorami liczb
Liczy naturalne różnią się od innych zbiorów liczb, takich jak liczby całkowite, wymierne czy rzeczywiste. Naturalne liczby są zawsze nieujemne, co oznacza, że nie zawierają liczb ujemnych ani ułamków. Z kolei zbiór liczb całkowitych $$\mathbb{Z}$$ obejmuje zarówno liczby dodatnie, jak i ujemne, a także zero. Liczby wymierne $$\mathbb{Q}$$ to liczby, które można zapisać w postaci ułamka, co oznacza, że mogą być zarówno całkowite, jak i dziesiętne.
W odróżnieniu od liczb naturalnych, które są ograniczone do wartości całkowitych nieujemnych, liczby rzeczywiste $$\mathbb{R}$$ obejmują wszystkie możliwe wartości na osi liczbowej, w tym liczby niewymierne. To sprawia, że liczby naturalne są bardzo specyficzne w swojej naturze, co czyni je użytecznymi w kontekście rozwiązywania równań, gdzie często poszukujemy wartości całkowitych.
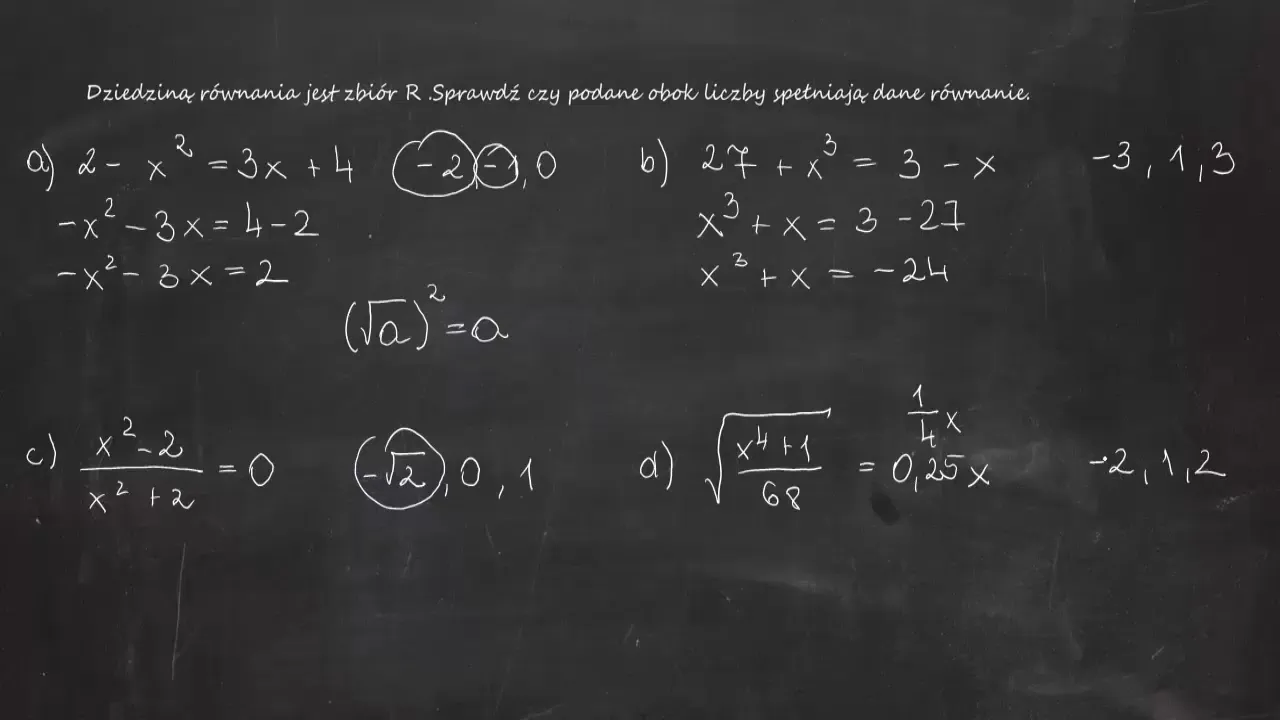
Metody rozwiązywania równań z liczbami naturalnymi
Rozwiązywanie równań z liczbami naturalnymi może być zrealizowane na różne sposoby, w zależności od rodzaju równania. Metody rozwiązywania równań obejmują zarówno podejścia algebraiczne, jak i graficzne. W przypadku równań liniowych, często stosuje się przekształcanie wyrażeń, aby uzyskać wartość zmiennej, która jest liczbą naturalną. W przypadku bardziej złożonych równań, takich jak kwadratowe, można również zastosować faktoryzację lub wzory kwadratowe, aby znaleźć rozwiązania.Inną popularną metodą jest stosowanie metody prób i błędów, gdzie różne wartości są podstawiane do równania, aż znajdzie się odpowiednia liczba naturalna, która spełnia równanie. Warto również korzystać z programów komputerowych lub kalkulatorów graficznych, które mogą pomóc w wizualizacji równań i szybszym znajdowaniu rozwiązań. W każdej z tych metod kluczowe jest, aby pamiętać o tym, że poszukujemy rozwiązań, które są liczbami naturalnymi.
- Algebraiczne przekształcanie: przekształcanie równań, aby znaleźć wartość zmiennej.
- Faktoryzacja: rozkładanie równań na iloczyny w celu znalezienia rozwiązań.
- Metoda prób i błędów: podstawianie różnych wartości do równania, aż znajdzie się odpowiednia liczba naturalna.
Analiza równań liniowych: krok po kroku do rozwiązania
Rozwiązywanie równań liniowych z liczbami naturalnymi można przeprowadzić w kilku prostych krokach. Po pierwsze, należy zapisać równanie w standardowej formie, na przykład $$ax + b = c$$. Następnie przekształcamy równanie, aby wydobyć zmienną $$x$$. Możemy to zrobić, odejmując $$b$$ od obu stron równania, a następnie dzieląc przez $$a$$. Kluczowe jest, aby w trakcie tych przekształceń zachować uwagę na to, czy uzyskana wartość $$x$$ jest liczbą naturalną.
Na przykład, rozważmy równanie $$2x + 3 = 7$$. Odejmujemy $$3$$ od obu stron, co daje $$2x = 4$$. Następnie dzielimy przez $$2$$, co prowadzi do $$x = 2$$. Liczba $$2$$ jest liczbą naturalną, więc to równanie ma rozwiązanie w zbiorze liczb naturalnych. Kluczowe jest, aby w każdym kroku upewnić się, że uzyskane rozwiązanie jest zgodne z wymaganiami zbioru liczb naturalnych.
Rozwiązywanie równań kwadratowych: przykłady i wskazówki
Równania kwadratowe mają postać $$ax^2 + bx + c = 0$$, gdzie $$a$$, $$b$$ i $$c$$ są stałymi, a $$a \neq 0$$. Istnieje kilka metod rozwiązywania takich równań, a jedną z najpopularniejszych jest stosowanie wzorów kwadratowych. Wzór kwadratowy pozwala na obliczenie miejsc zerowych równania i jest zapisany jako $$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$. Kluczowe jest, aby przed zastosowaniem tego wzoru upewnić się, że wyróżnik, czyli $$b^2 - 4ac$$, jest nieujemny, aby uzyskać rzeczywiste rozwiązania.Przykładem może być równanie $$2x^2 - 8x + 6 = 0$$. Tutaj $$a = 2$$, $$b = -8$$ i $$c = 6$$. Obliczamy wyróżnik: $$(-8)^2 - 4 \cdot 2 \cdot 6 = 64 - 48 = 16$$, co jest liczbą dodatnią. Stosując wzór kwadratowy, otrzymujemy $$x = \frac{8 \pm \sqrt{16}}{4} = \frac{8 \pm 4}{4}$$, co daje rozwiązania $$x = 3$$ oraz $$x = 1$$. Oba te wyniki są liczbami naturalnymi, co oznacza, że równanie spełnia wymagania dotyczące naturalnych rozwiązań.
- Wzory kwadratowe: $$x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}$$ - metoda uniwersalna dla równań kwadratowych.
- Faktoryzacja: przekształcanie równania do postaci iloczynowej, np. $$x^2 - 5x + 6 = (x - 2)(x - 3) = 0$$, co prowadzi do rozwiązań $$x = 2$$ i $$x = 3$$.
- Metoda dopełniania kwadratu: przekształcanie równania do postaci $$a(x - p)^2 = q$$, co ułatwia znalezienie miejsc zerowych.
Czytaj więcej: Jak się liczy logarytmy? Proste metody i przykłady obliczeń
Jak wykorzystać równania kwadratowe w codziennym życiu i pracy
Równania kwadratowe mają nie tylko zastosowanie w matematyce akademickiej, ale również w wielu praktycznych sytuacjach w życiu codziennym oraz w różnych dziedzinach zawodowych. Na przykład, inżynierowie wykorzystują równania kwadratowe do modelowania parabolicznych trajektorii, co jest kluczowe w projektowaniu elementów takich jak mosty czy drogi. Dzięki zrozumieniu, jak obliczać miejsca zerowe równania kwadratowego, można przewidzieć, jak obiekty będą się poruszać w przestrzeni, co ma ogromne znaczenie w inżynierii i architekturze.
Dodatkowo, analiza danych i statystyka często opierają się na równaniach kwadratowych, zwłaszcza w kontekście regresji kwadratowej. W takich przypadkach, wykorzystując równania kwadratowe, można modelować i przewidywać różne zjawiska, na przykład wzrost sprzedaży w zależności od kampanii marketingowych. Umiejętność rozwiązywania równań kwadratowych staje się zatem nie tylko przydatna w nauce, ale także cennym narzędziem w pracy zawodowej, umożliwiającym podejmowanie lepszych decyzji opartych na danych.