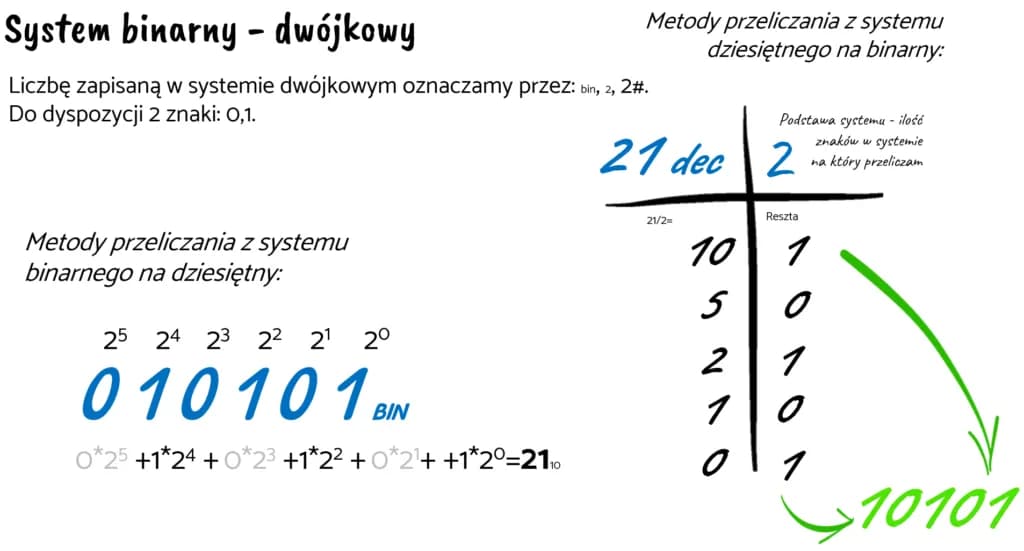
Jak zamieniać liczby binarne na dziesiętne to pytanie, które zadaje sobie wiele osób, zwłaszcza tych, którzy zaczynają swoją przygodę z programowaniem lub informatyką. System binarny, składający się jedynie z cyfr 0 i 1, jest podstawą działania komputerów. Aby przekształcić liczbę binarną na dziesiętną, należy zsumować wartości potęg liczby 2 dla każdej cyfry 1 w liczbie binarnej.
W tym artykule przedstawimy prostą metodę krok po kroku, która pozwoli Ci zrozumieć ten proces. Dzięki jasnym instrukcjom i praktycznym przykładom, nauczysz się, jak skutecznie zamieniać liczby binarne na dziesiętne, co jest przydatne w wielu dziedzinach, od programowania po elektronikę.
Kluczowe informacje:- System binarny składa się tylko z cyfr 0 i 1, podczas gdy system dziesiętny używa cyfr od 0 do 9.
- Aby zamienić liczbę binarną na dziesiętną, należy zsumować wartości potęg liczby 2 dla każdej cyfry 1.
- Analiza liczby binarnej polega na zrozumieniu jej struktury i pozycji cyfr.
- Obliczanie potęg liczby 2 jest kluczowym krokiem w procesie konwersji.
- Warto znać najczęstsze błędy przy konwersji, aby ich unikać i poprawnie wykonywać obliczenia.
Jak zamieniać liczby binarne na dziesiętne - podstawy konwersji
Systemy liczbowe to fundamentalne elementy matematyki i informatyki. System binarny, składający się tylko z cyfr 0 i 1, jest podstawą działania komputerów, podczas gdy system dziesiętny używa cyfr od 0 do 9. Zrozumienie różnic między tymi systemami jest kluczowe dla efektywnego konwertowania liczb z jednego systemu do drugiego.
Konwersja liczb binarnych na dziesiętne jest nie tylko teoretycznym zagadnieniem, ale ma również praktyczne zastosowania w codziennym życiu, zwłaszcza w dziedzinach takich jak programowanie i elektronika. Umiejętność ta pozwala na lepsze zrozumienie działania komputerów oraz procesów, które zachodzą w tle. Warto zatem poznać zasady rządzące tymi systemami, aby móc skutecznie przeprowadzać konwersje.
Zrozumienie systemu binarnego i dziesiętnego - kluczowe różnice
System binarny opiera się na dwóch cyfrach: 0 i 1. Każda cyfra w liczbie binarnej ma swoje miejsce i wartość, która jest potęgą liczby 2. Z kolei system dziesiętny, znany nam z codziennego użytku, wykorzystuje dziesięć cyfr, co sprawia, że jest bardziej intuicyjny dla większości ludzi. Ważne jest, aby zrozumieć, że różnice te wpływają na sposób, w jaki liczby są reprezentowane i obliczane.
Dlaczego warto znać metodę zamiany - praktyczne zastosowania
Znajomość metody zamiany liczb binarnych na dziesiętne jest niezwykle istotna w wielu dziedzinach, zwłaszcza w informatyce i elektronice. W codziennym użytkowaniu komputerów, programiści często muszą przekształcać dane z formatu binarnego na dziesiętny, aby zrozumieć, jak są one interpretowane przez maszyny. Na przykład, w programowaniu, konwersja ta jest kluczowa przy pracy z danymi, które są przechowywane w systemie binarnym.
W obszarze elektroniki, inżynierowie muszą często przeliczać wartości binarne na dziesiętne, aby poprawnie projektować układy cyfrowe. Znajomość konwersji pozwala na lepsze zrozumienie działania urządzeń, takich jak komputery, telefony czy systemy automatyki. Warto również zauważyć, że umiejętność ta jest przydatna w edukacji, gdzie uczniowie uczą się podstaw matematyki i logiki.
Prosta metoda krok po kroku do konwersji liczb
Konwersja liczb binarnych na dziesiętne może wydawać się skomplikowana, ale jest to proces, który można łatwo zrozumieć. Kluczowym krokiem jest analiza liczby binarnej, co pozwala na odczytanie jej wartości. Następnie, obliczamy potęgi liczby 2 dla każdej cyfry, co jest niezbędne do dalszych obliczeń. Ostatnim krokiem jest zsumowanie tych wartości, aby uzyskać wynik w systemie dziesiętnym.
W kolejnych częściach artykułu przedstawimy szczegółowe instrukcje dotyczące każdego z tych kroków, aby pomóc Ci w przyswojeniu tej umiejętności. Dzięki praktycznym przykładom i jasnym wytycznym, nauczysz się, jak skutecznie przeprowadzać konwersję, co otworzy przed Tobą nowe możliwości w pracy z danymi binarnymi.
Krok 1: Analiza liczby binarnej - jak ją odczytać
Aby skutecznie zamieniać liczby binarne na dziesiętne, pierwszym krokiem jest analiza liczby binarnej. Liczba binarna składa się z cyfr 0 i 1, gdzie każda cyfra ma swoje miejsce i wartość. Ważne jest, aby zrozumieć, że pozycja każdej cyfry w liczbie binarnej oznacza potęgę liczby 2. Na przykład w liczbie binarnej 1011, pierwsza cyfra od prawej (1) ma wartość 2^0, druga (1) ma wartość 2^1, trzecia (0) ma wartość 2^2, a czwarta (1) ma wartość 2^3.
Analizując liczbę binarną, można łatwo zidentyfikować, które cyfry są istotne dla dalszych obliczeń. Wartości cyfr 0 nie mają wpływu na wynik, dlatego skupiamy się tylko na cyfrach 1. Zrozumienie tej struktury jest kluczowe, ponieważ pozwala na prawidłowe przygotowanie do kolejnych kroków konwersji.
Krok 2: Obliczanie potęg liczby 2 - zasady działania
Drugim krokiem w procesie konwersji jest obliczanie potęg liczby 2 dla każdej cyfry w liczbie binarnej. Każda cyfra 1 w liczbie binarnej odpowiada konkretnej potędze liczby 2, w zależności od jej pozycji. Aby to zrobić, należy zacząć od prawej strony liczby i przypisać każdej cyfrze odpowiednią potęgę. Na przykład, dla liczby 1011, przypisujemy wartości: 2^3 dla pierwszej cyfry (1), 2^2 dla drugiej (0), 2^1 dla trzeciej (1) i 2^0 dla czwartej (1).
Obliczając te potęgi, uzyskujemy wartości, które są następnie wykorzystywane do sumowania. Warto pamiętać, że potęgi liczby 2 rosną eksponencjalnie, co oznacza, że każda kolejna cyfra ma wartość podwójną w porównaniu do poprzedniej. To zrozumienie jest niezbędne do skutecznego przeprowadzenia konwersji z systemu binarnego na dziesiętny.
Krok 3: Suma wartości potęg - jak uzyskać wynik dziesiętny
Ostatnim krokiem w procesie konwersji liczb binarnych na dziesiętne jest sumowanie wartości potęg liczby 2. Po obliczeniu potęg dla każdej cyfry 1 w liczbie binarnej, należy zsumować te wartości, aby uzyskać końcowy wynik w systemie dziesiętnym. Na przykład, jeśli mamy liczbę binarną 1011, obliczone potęgi to 2^3 (8), 2^2 (0), 2^1 (2) i 2^0 (1). W tym przypadku sumujemy tylko wartości odpowiadające cyfrze 1: 8 + 2 + 1.
Warto pamiętać, że cyfry 0 nie wpływają na sumę, dlatego można je pominąć w obliczeniach. Po zsumowaniu wszystkich istotnych wartości, otrzymujemy wynik, który jest odpowiednikiem liczby binarnej w systemie dziesiętnym. Ten proces jest kluczowy, ponieważ umożliwia zrozumienie, jak liczby binarne są przekształcane w bardziej zrozumiałe dla nas liczby dziesiętne, co jest niezbędne w wielu zastosowaniach technologicznych.
Czytaj więcej: Jak rozpoznać skok rozwojowy u dziecka i uniknąć frustracji rodziców
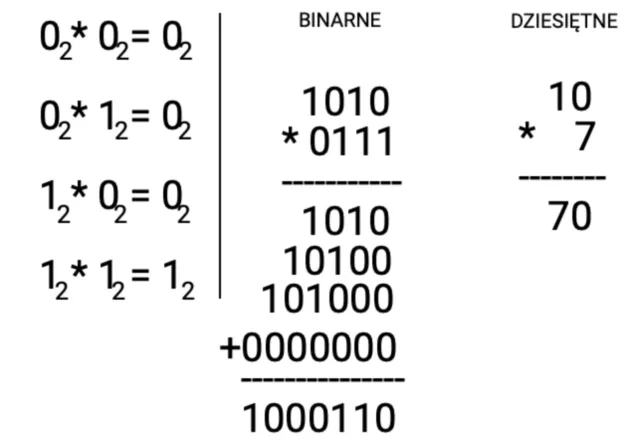
Przykłady konwersji - nauka przez praktykę
Aby lepiej zrozumieć proces konwersji, warto przyjrzeć się konkretnym przykładom. Zamiana liczb binarnych na dziesiętne pozwala na praktyczne zobrazowanie wcześniej omówionych kroków. W kolejnych częściach artykułu przedstawimy szczegółowe przykłady, które pomogą w utrwaleniu tej umiejętności.
Przykłady te będą ilustrować, jak każdy krok konwersji wpływa na ostateczny wynik. Dzięki nim, nauczysz się nie tylko, jak przeprowadzać konwersję, ale także zrozumiesz, dlaczego każdy krok jest istotny dla uzyskania poprawnego wyniku. Praktyka jest kluczem do opanowania tej umiejętności, dlatego zachęcamy do samodzielnego ćwiczenia konwersji liczb binarnych na dziesiętne.
Przykład 1: Zamiana liczby binarnej 1011 na dziesiętną
Aby zamienić liczbę binarną 1011 na system dziesiętny, zaczynamy od analizy każdej cyfry. Liczba ta składa się z cyfr 1, 0, 1 i 1, które odpowiadają kolejno potęgom liczby 2. Zaczynając od prawej, mamy: 20 (1), 21 (2), 22 (0) i 23 (8). Następnie sumujemy wartości potęg, które odpowiadają cyfrze 1: 8 + 2 + 1 = 11. Zatem liczba binarna 1011 w systemie dziesiętnym to 11.
Przykład 2: Zamiana liczby binarnej 11001 na dziesiętną
Przechodząc do liczby binarnej 11001, również analizujemy każdą cyfrę. W tej liczbie mamy cyfry 1, 1, 0, 0 i 1, które odpowiadają potęgom liczby 2. Od prawej strony, wartości potęg to: 20 (1), 21 (0), 22 (0), 23 (2) i 24 (16). Sumując wartości odpowiadające cyfrze 1, otrzymujemy 16 + 0 + 0 + 2 + 1 = 19. W związku z tym, liczba binarna 11001 w systemie dziesiętnym to 19.
Jak zrozumienie konwersji binarnej wpływa na programowanie i AI
Znajomość konwersji z systemu binarnego na dziesiętny ma kluczowe znaczenie nie tylko dla podstawowych obliczeń, ale także dla bardziej zaawansowanych zastosowań, takich jak programowanie i rozwój sztucznej inteligencji. W kontekście programowania, zrozumienie, jak liczby binarne są reprezentowane w pamięci komputera, pozwala programistom na optymalizację kodu oraz efektywne zarządzanie danymi. Na przykład, w językach programowania niskiego poziomu, takich jak C czy Assembly, programiści często muszą manipulować danymi w formacie binarnym, co wymaga solidnej wiedzy na temat konwersji.
W obszarze sztucznej inteligencji, konwersja binarna jest fundamentalna dla algorytmów uczenia maszynowego, które operują na danych w formacie binarnym. Zrozumienie tego procesu umożliwia lepszą interpretację wyników oraz przetwarzanie danych wejściowych. W przyszłości, z rozwojem technologii, umiejętność konwersji i analizy danych binarnych stanie się jeszcze bardziej istotna, zwłaszcza w kontekście analizy dużych zbiorów danych oraz przetwarzania sygnałów. Dlatego warto inwestować czas w rozwijanie tej umiejętności, co może przynieść korzyści w wielu dziedzinach zawodowych.