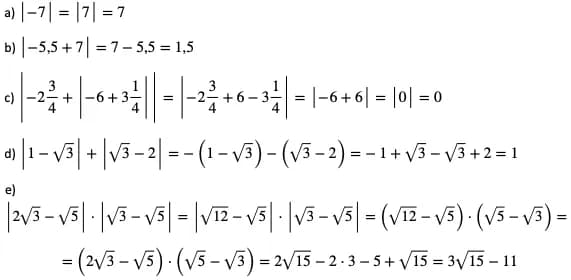Moduł w matematyce to pojęcie, które ma wiele znaczeń, ale najczęściej odnosi się do wartości bezwzględnej liczby rzeczywistej. Wartość bezwzględna, oznaczana jako |x|, jest liczbą, która ignoruje znak liczby, co oznacza, że zawsze jest nieujemna. Na przykład, wartość bezwzględna liczby 5 to 5, a wartość bezwzględna liczby -3 to 3. To pojęcie można również zrozumieć w kontekście geometrii, gdzie wartość bezwzględna reprezentuje odległość danej liczby od zera na osi liczbowej.
Dodatkowo, moduł można rozszerzyć na liczby zespolone, gdzie jego definicja przyjmuje formę |x + y · i| = √(x² + y²). Wartość ta jest istotna w analizie zespolonej i ma zastosowanie w różnych dziedzinach matematyki. Wreszcie, w algebrze, moduł to struktura, która generalizuje pojęcie przestrzeni liniowej, umożliwiając działanie pierścienia na grupie abelowej.
Kluczowe informacje:
- Wartość bezwzględna liczby rzeczywistej to jej odległość od zera na osi liczbowej.
- Definicja wartości bezwzględnej: |x| = x dla x ≥ 0 i |x| = -x dla x < 0.
- Moduł liczby zespolonej wyraża się wzorem: |x + y · i| = √(x² + y²).
- Termin „moduł” wprowadzono w 1806 roku przez Jean-Roberta Arganda.
- Moduły w algebrze są strukturami algebraicznymi, które rozszerzają pojęcie przestrzeni liniowej.
Definicja modułu w matematyce: Kluczowe pojęcie i jego znaczenie
Pojęcie modułu w matematyce odnosi się do wartości liczbowej, która nie uwzględnia znaku liczby. Najczęściej jest to związane z wartością bezwzględną, oznaczaną jako |x|. Moduł liczby rzeczywistej wskazuje na jej odległość od zera na osi liczbowej, co czyni go istotnym narzędziem w analizie matematycznej. Wartość bezwzględna jest definiowana w sposób prosty: dla liczby nieujemnej pozostaje ona bez zmian, natomiast dla liczby ujemnej przyjmuje wartość przeciwną. To fundamentalne pojęcie jest kluczowe dla zrozumienia bardziej złożonych zagadnień matematycznych.
W kontekście matematyki, moduł ma także zastosowanie w różnych dziedzinach, takich jak algebra czy analiza zespolona. Wartość bezwzględna jest nie tylko narzędziem do obliczeń, ale również kluczowym elementem w rozwiązywaniu równań i nierówności. Zrozumienie modułu jest zatem niezbędne dla każdego, kto pragnie zgłębiać tajniki matematyki i jej zastosowań w praktyce.
Wartość bezwzględna: Zrozumienie podstawowych zasad
Wartość bezwzględna liczby, oznaczana jako |x|, jest definiowana jako liczba, która zawsze jest nieujemna. Dla liczby nieujemnej, wartość bezwzględna jest równa samej liczbie, co można zapisać jako |x| = x dla x ≥ 0. Z kolei dla liczby ujemnej, wartość bezwzględna przyjmuje postać przeciwną, co oznacza, że |x| = -x dla x < 0. Przykłady ilustrujące te zasady to: |5| = 5, |-3| = 3, oraz |0| = 0.
Wartość bezwzględna ma kilka istotnych właściwości, które są kluczowe dla jej zastosowania w matematyce. Po pierwsze, jest zawsze nieujemna, co oznacza, że |x| ≥ 0 dla każdej liczby x. Po drugie, spełnia zasadę trójkąta, która mówi, że |x + y| ≤ |x| + |y|. Te właściwości czynią wartość bezwzględną niezwykle użytecznym narzędziem w analizie matematycznej oraz w rozwiązywaniu problemów związanych z równościami i nierównościami.
Geometria wartości bezwzględnej: Wizualizacja pojęcia
Wartość bezwzględna ma istotne znaczenie w kontekście geometrii, ponieważ można ją zobrazować na osi liczbowej. Na przykład, dla liczby 5, wartość bezwzględna |5| = 5 oznacza, że znajduje się ona pięć jednostek od zera. Z kolei wartość bezwzględna liczby -3, czyli |-3| = 3, wskazuje, że również jest oddalona o trzy jednostki od zera, ale w przeciwną stronę. Ta wizualizacja pomaga zrozumieć, że wartość bezwzględna zawsze odnosi się do odległości, co czyni ją niezmiennie nieujemną.
Na osi liczbowej, każda liczba ma swoją wartość bezwzględną, która jest reprezentowana jako odległość od zera. To podejście ułatwia zrozumienie pojęcia wartości bezwzględnej w praktyce. Aby zobrazować to zjawisko, można narysować prostą linię z zaznaczonymi punktami odpowiadającymi różnym liczbom oraz ich wartościami bezwzględnymi. Taka wizualizacja jest nie tylko pomocna w edukacji matematycznej, ale również w rozwiązywaniu problemów związanych z równościami i nierównościami.
| Numer | Wartość bezwzględna |
| 5 | |5| = 5 |
| -3 | |-3| = 3 |
| 0 | |0| = 0 |
Zastosowanie modułu w analizie zespolonej: Praktyczne przykłady
Moduł liczb zespolonych znajduje szerokie zastosowanie w analizie zespolonej, szczególnie w kontekście rozwiązywania równań i analizy funkcji. Na przykład, w teorii sygnałów, moduł jest używany do określenia amplitudy sygnału. W przypadku sygnału reprezentowanego jako liczba zespolona z = a + bi, gdzie a to część rzeczywista, a b to część urojona, jego moduł |z| = √(a² + b²) daje nam informację o jego amplitudzie. To zastosowanie jest kluczowe w telekomunikacji, gdzie amplituda sygnału wpływa na jakość transmisji.
Kolejnym przykładem jest zastosowanie modułu w obliczeniach związanych z transformacją Fouriera. Transformacja ta przekształca sygnały czasowe w reprezentację częstotliwościową, a moduł liczb zespolonych jest używany do określenia intensywności poszczególnych częstotliwości. W praktyce, jeśli mamy funkcję f(t) i jej transformację Fouriera F(ω), to moduł F(ω) wskazuje, jak silna jest dana częstotliwość w sygnale. Dzięki temu inżynierowie dźwięku mogą efektywnie analizować i przetwarzać dźwięki.
| Przykład | Zastosowanie |
| Amplituda sygnału | Określenie jakości sygnału w telekomunikacji |
| Transformacja Fouriera | Analiza intensywności częstotliwości w sygnale |
Własności modułu liczb zespolonych: Kluczowe cechy i zastosowania
Moduł liczb zespolonych posiada kilka kluczowych właściwości, które są istotne w analizie matematycznej. Po pierwsze, moduł liczb zespolonych spełnia zasadę trójkąta, co oznacza, że dla dowolnych dwóch liczb zespolonych z1 i z2, zachodzi nierówność |z1 + z2| ≤ |z1| + |z2|. Ta właściwość jest niezwykle ważna w kontekście analizy funkcji i rozwiązywania równań, ponieważ pozwala na oszacowanie wartości modułu sumy dwóch liczb zespolonych.
Kolejną istotną cechą jest to, że moduł liczby zespolonej jest równy zeru tylko wtedy, gdy sama liczba jest zerem. To znaczy, że |z| = 0 tylko wtedy, gdy z = 0. Ta właściwość jest kluczowa w kontekście rozwiązywania równań zespolonych oraz w teorii funkcji analitycznych, gdzie zrozumienie, kiedy funkcja przyjmuje wartość zerową, jest niezbędne do analizy jej zachowania.
Moduły w algebrze: Zrozumienie struktur algebraicznych
Moduł w matematyce to struktura algebraiczna, która jest uogólnieniem pojęcia przestrzeni wektorowej. Moduły pozwalają na działanie pierścienia na grupie abelowej, co oznacza, że skalarne mnożenie jest zdefiniowane w kontekście elementów z pierścienia. W przeciwieństwie do przestrzeni wektorowych, gdzie skalarami są liczby rzeczywiste lub zespolone, w modułach skalarami mogą być elementy z dowolnego pierścienia. To sprawia, że moduły są bardziej elastyczne i mogą być stosowane w szerszym zakresie sytuacji matematycznych.
Warto zauważyć, że moduły zachowują wiele właściwości przestrzeni wektorowych, takich jak rozdzielność i łączność. Oznacza to, że operacje w modułach są podobne do tych w przestrzeniach wektorowych, co pozwala na przenoszenie wielu technik i metod z jednego kontekstu do drugiego. Zrozumienie modułów jest kluczowe dla dalszych badań w algebrze, ponieważ stanowią one fundament dla bardziej zaawansowanych struktur algebraicznych, takich jak algebry asocjacyjne czy algebry Liego.
Różnice między modułami a przestrzeniami wektorowymi: Kluczowe porównania
Moduły i przestrzenie wektorowe różnią się głównie rodzajem skalarów, które mogą być używane do mnożenia elementów. W przestrzeniach wektorowych skalarami są liczby z ciała, co oznacza, że muszą spełniać określone aksjomaty, takie jak istnienie odwrotności do mnożenia. Natomiast w modułach skalarami mogą być elementy z pierścienia, który niekoniecznie musi mieć wszystkie te właściwości, co prowadzi do większej różnorodności w strukturach algebraicznych. Na przykład, w module nad pierścieniem całkowitych liczb, nie możemy znaleźć odwrotności dla wszystkich elementów, co różni go od przestrzeni wektorowej.
Inną istotną różnicą jest to, że przestrzenie wektorowe są zamknięte na operacje liniowe, podczas gdy moduły mogą być bardziej złożone w swoim zachowaniu. W przestrzeni wektorowej, każda kombinacja liniowa wektorów jest również wektorem w tej samej przestrzeni, podczas gdy w module, wynik operacji może nie należeć do modułu, jeśli nie spełnia określonych warunków. To sprawia, że analiza modułów wymaga bardziej złożonych narzędzi i technik w porównaniu do przestrzeni wektorowych, co czyni je interesującym obszarem badań w algebrze.
Przykłady zastosowań modułów w różnych dziedzinach matematyki
Moduły znajdują zastosowanie w wielu dziedzinach matematyki, w tym w teorii liczb, algebrze oraz w analizie matematycznej. Na przykład, w teorii liczb, moduły są używane do badania struktur algebraicznych, takich jak pierścienie całkowite. W kontekście algebry, moduły nad pierścieniami umożliwiają zrozumienie właściwości grup abelowych i ich relacji z innymi strukturami algebraicznymi. Dzięki temu matematycy mogą analizować i klasyfikować liczby w bardziej złożony sposób, co jest kluczowe w zaawansowanych badaniach matematycznych.
Innym przykładem zastosowania modułów jest ich wykorzystanie w analizie funkcji. Moduły pozwalają na zrozumienie zachowania funkcji w kontekście rozwiązywania równań różniczkowych i całkowych. Na przykład, w zastosowaniach inżynieryjnych, moduły są używane do modelowania systemów dynamicznych, gdzie analiza funkcji jest niezbędna do przewidywania zachowania systemu w czasie. Moduły umożliwiają matematykom i inżynierom tworzenie bardziej precyzyjnych modeli, które są kluczowe w projektowaniu i optymalizacji systemów.
- Teoria liczb: Moduły pomagają w badaniu struktur algebraicznych, takich jak pierścienie całkowite.
- Analiza funkcji: Moduły są używane do rozwiązywania równań różniczkowych i całkowych w kontekście inżynieryjnym.
- Modelowanie systemów dynamicznych: Moduły umożliwiają tworzenie precyzyjnych modeli dla przewidywania zachowania systemów.
Czytaj więcej: Sytuacje zadaniowe w matematyce, które zmienią twoje nauczanie
Moduły w matematyce: Nowe kierunki w zastosowaniach technologicznych
W miarę jak technologia rozwija się, moduły w matematyce znajdują coraz więcej zastosowań w dziedzinach takich jak sztuczna inteligencja i uczenie maszynowe. Na przykład, w algorytmach uczenia maszynowego, moduły mogą być wykorzystywane do analizy danych w kontekście przestrzeni cech, co pozwala na lepsze modelowanie złożonych problemów. Przez zastosowanie modułów, inżynierowie mogą tworzyć bardziej efektywne algorytmy, które są w stanie przetwarzać i analizować duże zbiory danych, co jest kluczowe w dobie big data.
Dodatkowo, moduły mogą odgrywać ważną rolę w kryptografii, gdzie ich struktury algebraiczne mogą być wykorzystywane do tworzenia bardziej bezpiecznych systemów szyfrowania. Zrozumienie właściwości modułów pozwala na rozwijanie nowych metod zabezpieczania informacji, co jest szczególnie istotne w kontekście rosnących zagrożeń cybernetycznych. W ten sposób, badania nad modułami nie tylko poszerzają naszą wiedzę teoretyczną, ale także mają praktyczne implikacje w nowoczesnych technologiach.
