Wektory w matematyce to fundamentalny temat, który odgrywa kluczową rolę w różnych dziedzinach nauki i inżynierii. Są to uporządkowane pary punktów, które tworzą strzałkę wyznaczoną przez dwa punkty. Wektory mają trzy główne cechy: długość, kierunek i zwrot, które są niezbędne do ich zrozumienia i zastosowania w praktyce.
W niniejszym artykule przyjrzymy się bliżej definicji wektorów oraz ich znaczeniu w matematyce, a także omówimy ich właściwości, metody reprezentacji oraz operacje, które można na nich wykonywać. Zrozumienie wektorów jest nie tylko istotne dla studentów matematyki, ale także dla osób pracujących w dziedzinach takich jak fizyka czy inżynieria, gdzie wektory są wykorzystywane do opisu ruchu, sił i kształtów.
Kluczowe informacje:- Wektory są reprezentowane jako uporządkowane pary punktów i mają długość, kierunek oraz zwrot.
- Długość wektora można obliczyć za pomocą twierdzenia Pitagorasa.
- Kierunek i zwrot wektora mają kluczowe znaczenie w jego reprezentacji i zastosowaniach.
- Wektory mogą być przedstawiane graficznie w układzie współrzędnych oraz zapisywane w różnych notacjach matematycznych.
- Podstawowe operacje na wektorach obejmują dodawanie, odejmowanie oraz mnożenie przez skalar.
- Wektory znajdują zastosowanie w geometrii, fizyce oraz technologii, w tym w grafice komputerowej.
- Przykłady zastosowania wektorów w codziennym życiu obejmują nawigację oraz analizę ruchu.
Wektory w matematyce - definicja i podstawowe pojęcia
Wektory w matematyce są podstawowymi obiektami, które odgrywają kluczową rolę w różnych dziedzinach, takich jak geometria, fizyka czy inżynieria. Definiuje się je jako uporządkowane pary punktów, które tworzą strzałkę wyznaczoną przez dwa punkty. Wektory mają trzy główne cechy: długość, kierunek oraz zwrot, które są istotne do ich analizy i zastosowania.
W matematyce wektory są używane do reprezentacji wielkości, które mają zarówno wartość, jak i kierunek. Dzięki nim można opisywać różne zjawiska, takie jak ruch obiektów czy siły działające na ciało. Zrozumienie wektorów jest niezbędne dla każdego, kto chce zgłębić bardziej zaawansowane zagadnienia matematyczne i fizyczne.
Czym są wektory w matematyce i jakie mają znaczenie?
Wektory stanowią fundamentalny element matematyki, umożliwiając precyzyjne opisanie zjawisk, które wymagają uwzględnienia kierunku. Na przykład, w fizyce wektory są używane do opisu sił, prędkości czy przyspieszeń, co czyni je niezastąpionymi w analizie ruchu. W matematyce wektory pozwalają również na modelowanie złożonych struktur i relacji w przestrzeni.
W praktyce, wektory są wykorzystywane w wielu zastosowaniach, od inżynierii po grafikę komputerową. Dzięki nim można tworzyć realistyczne modele i symulacje, które oddają rzeczywiste zachowanie obiektów w przestrzeni. W ten sposób wektory nie tylko ułatwiają zrozumienie skomplikowanych zjawisk, ale także mają zastosowanie w codziennym życiu, na przykład w nawigacji czy projektowaniu.
Właściwości wektorów - zrozumienie kluczowych cech
Wektory mają kilka fundamentalnych właściwości, które są kluczowe dla ich zrozumienia i zastosowania w matematyce. Pierwszą z tych właściwości jest długość, która określa, jak daleko rozciąga się wektor od jednego punktu do drugiego. Długość wektora jest ważna, ponieważ pozwala na ocenę wielkości reprezentowanej przez dany wektor, co jest istotne w wielu dziedzinach, takich jak fizyka czy inżynieria.
Kolejną istotną cechą wektorów jest ich kierunek oraz zwrot. Kierunek wektora wskazuje, w którą stronę jest on skierowany, natomiast zwrot określa, czy wektor jest skierowany w stronę dodatnią, czy ujemną. Te dwa aspekty są kluczowe w kontekście analizy ruchu, gdzie kierunek i zwrot sił mają ogromne znaczenie dla zrozumienia dynamiki obiektów.
Długość wektora - jak ją obliczyć i co oznacza?
Długość wektora można obliczyć przy użyciu twierdzenia Pitagorasa. W przypadku wektora w układzie współrzędnych, długość wektora (oznaczana jako |v|) można obliczyć za pomocą wzoru: |v| = √(x² + y²), gdzie x i y to współrzędne końca wektora. Na przykład, jeśli wektor ma współrzędne (3, 4), jego długość wyniesie |v| = √(3² + 4²) = √(9 + 16) = √25 = 5.
Kierunek i zwrot wektora - ich rola w matematyce
Kierunek i zwrot wektora są kluczowymi cechami, które wpływają na jego reprezentację i zastosowanie w matematyce. Kierunek odnosi się do orientacji wektora w przestrzeni, wskazując, w którą stronę jest on skierowany. Na przykład, wektor skierowany w prawo ma inny kierunek niż wektor skierowany w lewo, mimo że mogą mieć tę samą długość.Natomiast zwrot wektora określa, czy wektor jest skierowany w stronę dodatnią czy ujemną. Może to mieć znaczenie w kontekście analizy ruchu, gdzie zwrot wektora siły może decydować o tym, czy obiekt przyspiesza, czy zwalnia. W praktyce, zrozumienie kierunku i zwrotu wektora jest niezbędne do poprawnego modelowania zjawisk fizycznych i matematycznych.
Czytaj więcej: Jak szkoły wykorzystują filmy w edukacji społecznej?
Reprezentacja wektorów - różne metody i notacje
Wektory można reprezentować na różne sposoby, zarówno graficznie, jak i algebraicznie. Graficzna reprezentacja wektora polega na narysowaniu go jako strzałki w układzie współrzędnych, gdzie długość strzałki odpowiada długości wektora, a kierunek wskazuje jego orientację. W notacji algebraicznej wektory często zapisuje się jako uporządkowane pary liczb, na przykład v = (x, y), gdzie x i y to współrzędne końca wektora.Ważne jest, aby wybrać odpowiednią metodę reprezentacji wektora w zależności od kontekstu, w jakim jest używany. W matematyce i fizyce, zarówno graficzne, jak i algebraiczne formy reprezentacji są niezbędne do analizy i rozwiązania problemów związanych z wektorami.
Wektory w układzie współrzędnych - graficzne przedstawienie
Wektory w matematyce można graficznie przedstawiać w układzie współrzędnych, co pozwala na wizualizację ich długości i kierunku. W takim przedstawieniu wektor jest rysowany jako strzałka, której początek znajduje się w punkcie (0,0) (lub innym punkcie, w zależności od kontekstu), a koniec wskazuje na współrzędne końcowe wektora. Na przykład, wektor o współrzędnych (3, 4) będzie miał początek w punkcie (0,0) i kończyć się w punkcie (3,4), co można zobaczyć na graficznym wykresie.
Graficzna reprezentacja wektorów jest nie tylko intuicyjna, ale także ułatwia zrozumienie złożonych relacji między różnymi wektorami. Dzięki wizualizacji można łatwo dostrzec, jak wektory współdziałają ze sobą, co jest kluczowe w wielu zastosowaniach matematycznych i inżynieryjnych.
Notacja wektorowa - jak zapisywać wektory matematycznie?
W matematyce wektory zapisywane są w różnych formatach, co ułatwia ich analizę i obliczenia. Najczęściej używaną notacją jest notacja współrzędnych, gdzie wektor zapisuje się jako v = (x, y), gdzie x i y to współrzędne końca wektora. Innym sposobem zapisu jest użycie symboli, na przykład v = ai + bj, gdzie a i b to składowe wektora w kierunkach osi X i Y, a i oraz j to jednostkowe wektory w tych kierunkach.
Wybór odpowiedniej notacji zależy od kontekstu, w jakim wektory są używane. W zastosowaniach inżynieryjnych często korzysta się z notacji z jednostkowymi wektorami, podczas gdy w matematyce czysto teoretycznej preferuje się zapisy współrzędne. Zrozumienie różnych formatów notacji jest kluczowe dla efektywnej pracy z wektorami w różnych dziedzinach.
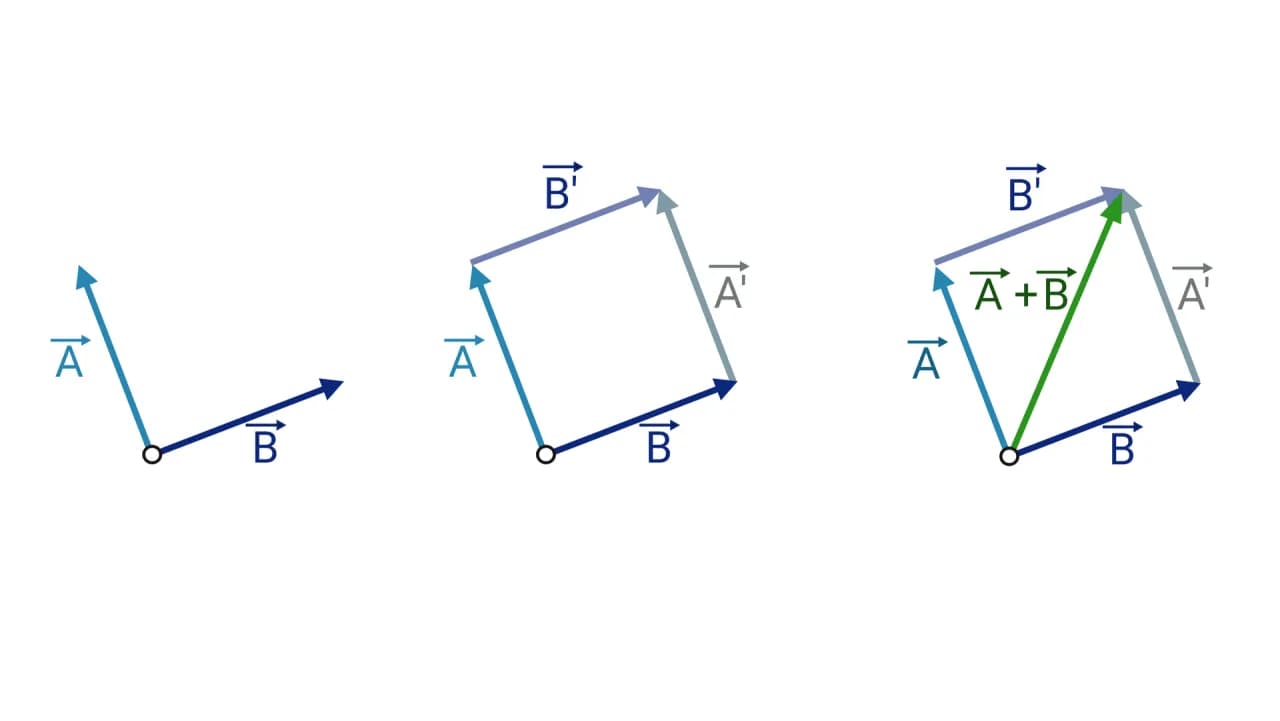
Operacje na wektorach - podstawy i zaawansowane techniki
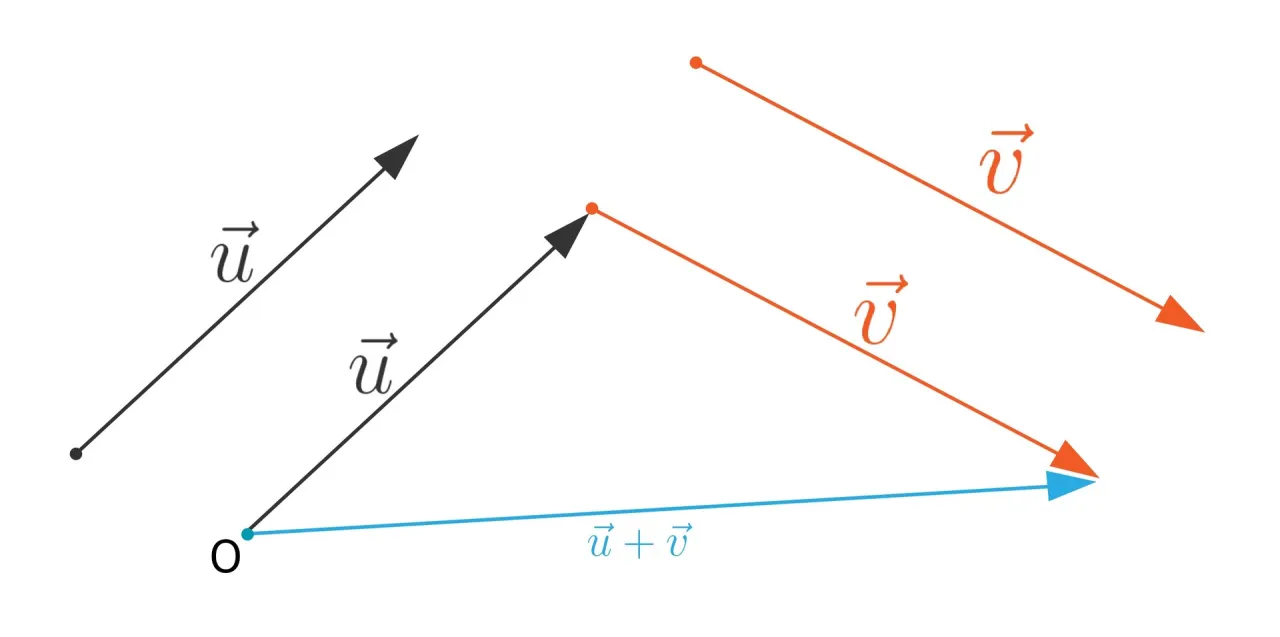
Operacje na wektorach są kluczowe dla zrozumienia ich zastosowań w matematyce i fizyce. Wśród podstawowych operacji znajdują się dodawanie i odejmowanie wektorów, które pozwalają na łączenie różnych wektorów w jedną całość. Te operacje są niezbędne do analizy zjawisk, takich jak ruch obiektów czy siły działające na nie, a ich zrozumienie stanowi fundament dla bardziej skomplikowanych technik.
Zaawansowane techniki obejmują mnożenie wektora przez skalar, co zmienia długość wektora, ale nie jego kierunek. Dzięki tym operacjom można manipulować wektorami w różnych kontekstach, co jest szczególnie przydatne w inżynierii i grafice komputerowej. W kolejnych sekcjach przyjrzymy się szczegółowo zasadom dodawania i odejmowania wektorów oraz ich praktycznym zastosowaniom.
Dodawanie i odejmowanie wektorów - zasady i przykłady
Dodawanie wektorów polega na łączeniu ich składowych. Na przykład, jeśli mamy wektor A = (2, 3) i wektor B = (4, 5), to ich suma C = A + B będzie wynosić C = (2 + 4, 3 + 5) = (6, 8). W praktyce oznacza to, że końcowy wektor C jest przesunięciem, które łączy przesunięcia reprezentowane przez wektory A i B. Z kolei odejmowanie wektorów działa na zasadzie dodawania wektora przeciwnym kierunku. Dla wektora A = (2, 3) i wektora B = (4, 5), różnica D = A - B będzie wynosić D = (2 - 4, 3 - 5) = (-2, -2).
Praktyczne zastosowania wektorów w nowoczesnej technologii
Wektory znajdują zastosowanie nie tylko w klasycznej matematyce i fizyce, ale także w wielu nowoczesnych technologiach, takich jak grafika komputerowa, uczenie maszynowe oraz robotyka. W kontekście grafiki komputerowej, wektory są używane do modelowania obiektów 2D i 3D, co pozwala na tworzenie realistycznych animacji i efektów wizualnych. Dzięki wektorom, projektanci mogą łatwo skalować obrazy bez utraty jakości, co jest kluczowe w dzisiejszym świecie cyfrowym.
W dziedzinie uczenia maszynowego, wektory są wykorzystywane do reprezentacji danych w przestrzeni wielowymiarowej, co umożliwia algorytmom lepsze zrozumienie złożonych wzorców i relacji. W robotyce, wektory pomagają w nawigacji i planowaniu ruchu, umożliwiając robotom precyzyjne poruszanie się w przestrzeni. Zrozumienie, jak wektory funkcjonują w tych nowoczesnych aplikacjach, otwiera nowe możliwości dla inżynierów i programistów, którzy mogą wykorzystać te narzędzia do tworzenia innowacyjnych rozwiązań technologicznych.