Odcinek w matematyce to pojęcie, które odnosi się do segmentu linii pomiędzy dwoma punktami. Jest to podstawowy element geometrii, który ma stałą długość. Zrozumienie, czym jest odcinek oraz jak obliczyć jego długość, jest kluczowe dla wielu dziedzin matematyki. W tym artykule przyjrzymy się definicji odcinka, jego właściwościom oraz metodom obliczania długości, korzystając z odpowiednich wzorów.
Obliczanie długości odcinka jest szczególnie istotne w kontekście układów współrzędnych, gdzie można zastosować wzór na długość odcinka. Dzięki temu narzędziu matematycznemu, możliwe jest nie tylko wyznaczenie długości, ale także zrozumienie, jak odcinki funkcjonują w przestrzeni. Przygotowaliśmy praktyczne przykłady, które pomogą w lepszym zrozumieniu tego zagadnienia.
Kluczowe informacje:- Odcinek w matematyce to segment linii między dwoma punktami o stałej długości.
- Właściwości odcinka obejmują jego długość, prostoliniowość oraz unikalność.
- Długość odcinka można obliczyć za pomocą wzoru na długość odcinka w układzie współrzędnych.
- Przykłady obliczeń długości odcinka w układzie kartezjańskim są kluczowe dla zrozumienia praktycznego zastosowania wzoru.
- Odcinki mają zastosowanie w różnych dziedzinach, takich jak architektura czy inżynieria.
Definicja odcinka w matematyce i jego podstawowe cechy
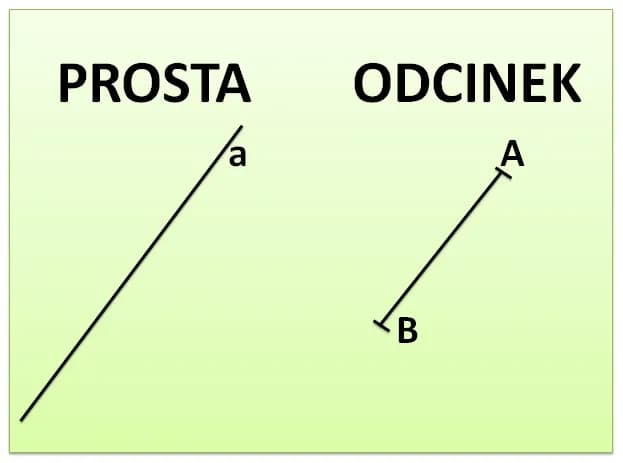
Odcinek w matematyce to segment linii, który łączy dwa punkty. Jest to fundamentalny element geometrii, który charakteryzuje się stałą długością. Odcinek różni się od innych elementów geometrycznych, takich jak linie czy krzywe, ponieważ ma wyraźnie określone końce, co czyni go unikalnym w kontekście analizy przestrzennej.
Właściwości odcinka obejmują jego długość, prostoliniowość oraz unikalność. Odcinek jest zawsze prosty, co oznacza, że nie ma zakrętów ani zagięć. Każdy odcinek można opisać za pomocą współrzędnych jego końców, co pozwala na jego analizę w różnych układach współrzędnych, takich jak układ kartezjański.
Odcinek jako element geometrii: Co to jest?
Odcinek jest podstawowym pojęciem w geometrii, definiowanym jako część linii, która ma dwa końce. Te końce, nazywane punktami końcowymi, są kluczowe dla zrozumienia, co to jest odcinek. Można go wizualizować jako najkrótszą drogę między tymi dwoma punktami, co czyni go istotnym w wielu zastosowaniach matematycznych oraz praktycznych.
W geometrii, odcinek jest często reprezentowany za pomocą liter, które oznaczają jego końce, na przykład odcinek AB jest reprezentowany przez dwa punkty A i B. Odcinki mogą być różnej długości i są niezbędne w analizie kształtów oraz w rozwiązywaniu problemów geometrycznych.
Jakie są kluczowe właściwości odcinka w matematyce?
Odcinek w matematyce ma kilka kluczowych właściwości, które są istotne dla jego zrozumienia i analizy. Po pierwsze, odcinek ma stałą długość, co oznacza, że jest to najkrótsza droga między dwoma punktami. Po drugie, odcinek jest zawsze prostoliniowy, co oznacza, że nie zawiera żadnych zakrętów ani zagięć. Wreszcie, każdy odcinek jest unikalny, co oznacza, że nie można go pomylić z innym odcinkiem, gdyż ma wyraźnie określone końce.
Te właściwości odcinka są podstawą wielu obliczeń i zastosowań w matematyce oraz w dziedzinach pokrewnych. Zrozumienie ich jest kluczowe dla dalszej analizy i wykorzystania odcinków w różnych kontekstach matematycznych.
- Długość: Odcinek ma stałą długość, co czyni go łatwym do zdefiniowania i pomiaru.
- Prostoliniowość: Odcinek jest najkrótszą drogą między dwoma punktami, co oznacza, że zawsze jest prosty.
- Unikalność: Każdy odcinek ma swoje unikalne punkty końcowe, co pozwala na jego jednoznaczną identyfikację.
- Reprezentacja: Odcinek można reprezentować w układzie współrzędnych, co ułatwia jego analizę.
- Wykorzystanie: Odcinki są wykorzystywane w różnych dziedzinach, takich jak geografia, architektura czy inżynieria.
Metody obliczania długości odcinka w matematyce
Obliczanie długości odcinka jest fundamentalnym zagadnieniem w matematyce. Istnieją różne metody, które pozwalają na dokładne wyznaczenie długości, a najpopularniejszą z nich jest wzór na długość odcinka. Ten wzór opiera się na współrzędnych końcowych odcinka i pozwala na szybkie i efektywne obliczenia. Zrozumienie, jak korzystać z tego wzoru, jest kluczowe dla każdego, kto zajmuje się geometrią lub innymi dziedzinami matematycznymi.Ważne jest, aby zrozumieć, że długość odcinka można obliczyć w różnych układach współrzędnych. Dzięki temu można zastosować różne techniki i narzędzia do analizy odcinków w kontekście przestrzennym. W kolejnych częściach artykułu przyjrzymy się konkretnym metodom obliczania długości odcinka oraz zastosowaniom wzoru w praktyce.
Wprowadzenie do wzoru na długość odcinka: Co musisz wiedzieć?
W matematyce, aby obliczyć długość odcinka, stosuje się wzór na długość odcinka. Jest to kluczowe narzędzie, które pozwala na dokładne określenie odległości między dwoma punktami w przestrzeni. Wzór ten opiera się na współrzędnych końcowych odcinka i wykorzystuje teoretyczne podstawy geometrii analitycznej. Dzięki temu, można skutecznie obliczyć długość odcinka w różnych układach współrzędnych, takich jak układ kartezjański.
Wzór na długość odcinka jest wyrażany jako pierwiastek kwadratowy z sumy kwadratów różnic współrzędnych punktów końcowych. Zrozumienie poszczególnych elementów tego wzoru jest niezbędne do jego prawidłowego zastosowania. W kolejnych sekcjach przedstawimy, jak krok po kroku wykorzystać ten wzór w praktyce.
Krok po kroku: Jak zastosować wzór w praktyce?
Obliczanie długości odcinka za pomocą wzoru wymaga kilku prostych kroków. Na początku należy zidentyfikować współrzędne punktów końcowych odcinka. Następnie, używając wzoru, można obliczyć długość odcinka. Poniżej przedstawiamy szczegółowy opis kroków, które należy wykonać.
- Krok 1: Zidentyfikuj współrzędne punktów końcowych odcinka, np. A(x1, y1) i B(x2, y2).
- Krok 2: Oblicz różnicę między współrzędnymi x: Δx = x2 - x1.
- Krok 3: Oblicz różnicę między współrzędnymi y: Δy = y2 - y1.
- Krok 4: Zastosuj wzór: długość odcinka = √(Δx² + Δy²).
- Krok 5: Oblicz pierwiastek kwadratowy z sumy kwadratów różnic, aby uzyskać długość odcinka.
| Współrzędne A | (3, 4) |
| Współrzędne B | (7, 1) |
| Δx | 7 - 3 = 4 |
| Δy | 1 - 4 = -3 |
| Długość odcinka | √(4² + (-3)²) = √(16 + 9) = √25 = 5 |
Czytaj więcej: Najskuteczniejsze metody nauczania języka angielskiego - poznaj 6 sposobów
Przykłady obliczeń długości odcinka w różnych układach
Obliczanie długości odcinka w różnych układach współrzędnych jest istotnym zagadnieniem w matematyce. Umożliwia to nie tylko zrozumienie, jak odcinki funkcjonują w przestrzeni, ale także praktyczne zastosowanie wzorów w różnych kontekstach. Przykłady te pomagają w lepszym zrozumieniu, jak wykorzystać wzór na długość odcinka w rzeczywistych sytuacjach.
W szczególności, obliczanie długości odcinka w układzie kartezjańskim jest jednym z najczęściej stosowanych przypadków. W tym układzie, współrzędne punktów końcowych odcinka są wyrażane jako pary liczb (x, y), co ułatwia zastosowanie wzoru na długość. W kolejnych akapitach przedstawimy konkretne przykłady obliczeń długości odcinka w tym układzie.Obliczanie długości odcinka w układzie kartezjańskim
Aby obliczyć długość odcinka w układzie kartezjańskim, należy najpierw zidentyfikować współrzędne jego końców. Następnie, korzystając z wzoru na długość odcinka, można szybko i efektywnie wyznaczyć odległość między tymi punktami. Wzór ten oparty jest na różnicach współrzędnych x i y punktów końcowych.
Na przykład, rozważmy odcinek łączący punkty A(2, 3) i B(5, 7). Aby obliczyć długość tego odcinka, należy wykonać następujące kroki:
- Zidentyfikować współrzędne punktów: A(2, 3) i B(5, 7).
- Obliczyć różnicę między współrzędnymi x: Δx = 5 - 2 = 3.
- Obliczyć różnicę między współrzędnymi y: Δy = 7 - 3 = 4.
- Zastosować wzór: długość odcinka = √(Δx² + Δy²) = √(3² + 4²) = √(9 + 16) = √25 = 5.
W rezultacie, długość odcinka AB wynosi 5 jednostek. Tego typu obliczenia są kluczowe w geometrii i mają zastosowanie w wielu dziedzinach, takich jak inżynieria czy architektura.
Przykłady zastosowania odcinka w zadaniach matematycznych
Odcinki w matematyce mają szerokie zastosowanie w różnych problemach i zadaniach. Są one nie tylko fundamentem geometrii, ale także pojawiają się w praktycznych sytuacjach, takich jak obliczenia w architekturze, inżynierii czy grafice komputerowej. Zrozumienie, jak wykorzystać odcinek w matematyce, pozwala na skuteczne rozwiązywanie problemów i analizę danych.
Przykładowo, odcinki są często używane do obliczeń związanych z odległościami w układzie współrzędnych. W kontekście geometrii analitycznej, można je zastosować do obliczeń dotyczących kątów, obwodów czy powierzchni figur geometrycznych. Poniżej przedstawiamy kilka konkretnych przykładów zastosowania odcinków w zadaniach matematycznych.- Obliczanie odległości między punktami: Odcinki są używane do wyznaczania odległości pomiędzy dwoma punktami w układzie kartezjańskim przy użyciu wzoru na długość odcinka.
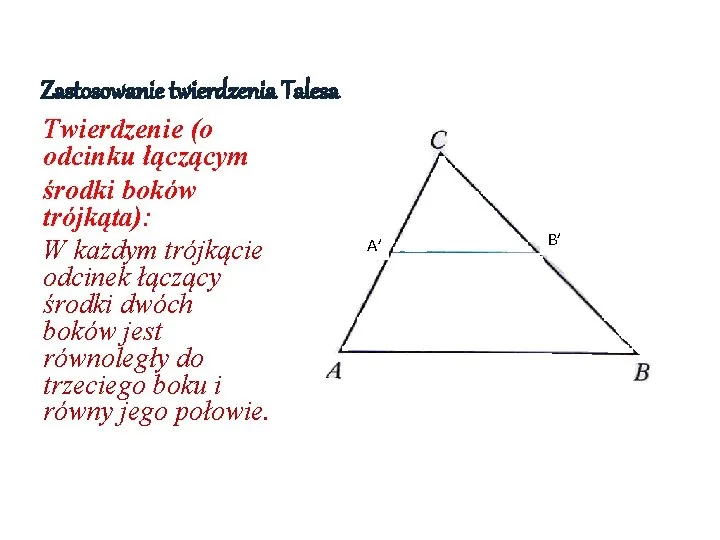
- Analiza kątów: Odcinki mogą być stosowane do obliczeń kątów w trójkątach, gdzie długości boków są odcinkami.
- Modelowanie w inżynierii: W inżynierii, odcinki są używane do modelowania struktur i obliczania ich stabilności oraz wytrzymałości.
Praktyczne zastosowanie odcinków w modelowaniu 3D i grafice komputerowej
Odcinki w matematyce nie tylko służą do obliczania odległości, ale również odgrywają kluczową rolę w modelowaniu 3D oraz grafice komputerowej. W tych dziedzinach, odcinki są wykorzystywane do tworzenia i definiowania kształtów obiektów, co umożliwia realistyczne odwzorowanie rzeczywistości. Dzięki odcinkom, programiści i projektanci mogą precyzyjnie określać krawędzie i kontury obiektów, co jest niezbędne w procesie renderowania.
Przykładowo, w grach komputerowych i aplikacjach VR, odcinki są wykorzystywane do obliczeń związanych z kolizjami i interakcjami między obiektami. Umożliwia to płynne i realistyczne poruszanie się postaci oraz interakcję z otoczeniem. Zrozumienie i umiejętność pracy z odcinkami w kontekście grafiki komputerowej otwiera nowe możliwości dla twórców, pozwalając na tworzenie bardziej złożonych i atrakcyjnych wizualnie projektów.