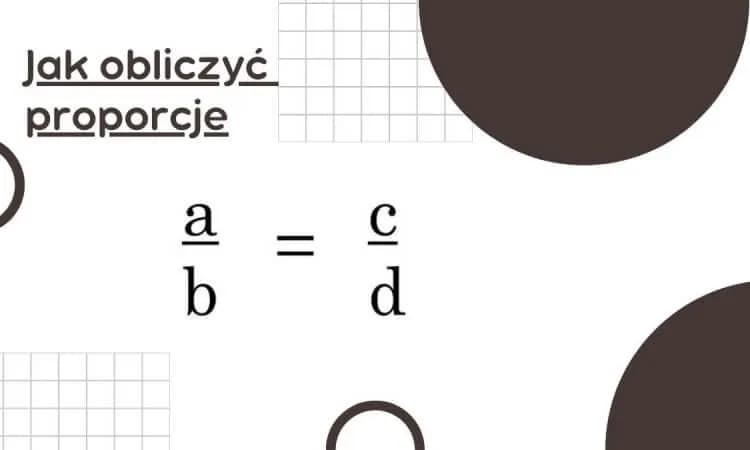Obliczanie proporcji w matematyce to kluczowa umiejętność, która pozwala na zrozumienie relacji między różnymi wielkościami. Proporcje można zapisać jako równość dwóch ilorazów, co oznacza, że możemy porównywać różne wartości i określać ich wzajemne zależności. Na przykład, jeśli mamy proporcję a:b = c:d, to a i d są wyrazami skrajnymi, a b i c są wyrazami środkowymi. Zrozumienie tego zagadnienia jest nie tylko istotne w kontekście matematyki, ale także w codziennym życiu, gdzie często korzystamy z proporcji w różnych sytuacjach, takich jak gotowanie czy zakupy.
W tym artykule przedstawimy proste metody obliczania proporcji oraz przykłady, które pomogą Ci lepiej zrozumieć ten temat. Dowiesz się, jak rozwiązywać proporcje krok po kroku, a także jakie zastosowania mają one w praktyce, zarówno w handlu, jak i w naukach przyrodniczych. Dzięki wizualizacjom i narzędziom wspierającym obliczanie proporcji, nauka stanie się jeszcze łatwiejsza i bardziej przystępna. Kluczowe informacje:- Proporcje to równości dwóch ilorazów, które umożliwiają porównywanie wartości.
- Wzór proporcji można zapisać jako a:b = c:d, gdzie a i d to wyrazy skrajne, a b i c to wyrazy środkowe.
- Obliczanie proporcji jest istotne w codziennych sytuacjach, takich jak gotowanie, zakupy czy planowanie budżetu.
- W artykule omówione zostaną metody rozwiązywania proporcji oraz konkretne przykłady z różnych dziedzin matematyki.
- Proporcje mają zastosowanie w handlu, pomagając w ustalaniu cen i rabatów, oraz w naukach przyrodniczych, wspierając eksperymenty i badania.
- Wizualizacje i diagramy ułatwiają zrozumienie i obliczanie proporcji.
Zrozumienie podstaw obliczania proporcji w matematyce
Obliczanie proporcji w matematyce jest fundamentalnym zagadnieniem, które pozwala na zrozumienie relacji między różnymi wartościami. Proporcje to równości dwóch ilorazów, co oznacza, że możemy je zapisać w formie a:b = c:d. W tej notacji, a i d są wyrazami skrajnymi, natomiast b i c to wyrazy środkowe. Zrozumienie tego konceptu jest kluczowe, ponieważ umożliwia porównywanie różnych wielkości oraz ich wzajemne zależności.
W codziennym życiu spotykamy się z proporcjami na każdym kroku. Na przykład, przy gotowaniu potraw, często musimy dostosować składniki w odpowiednich proporcjach, aby uzyskać pożądany smak. Podobnie, w handlu, stosowanie proporcji pomaga w ustalaniu cen i rabatów. Dzięki znajomości proporcji, możemy lepiej zrozumieć otaczający nas świat i podejmować bardziej świadome decyzje.
Co to są proporcje i jak je definiujemy w matematyce?
Proporcje to relacje między dwiema wielkościami, które można wyrazić jako równość dwóch ilorazów. Na przykład, jeśli mamy proporcję 2:3 = 4:6, oznacza to, że stosunek 2 do 3 jest równy stosunkowi 4 do 6. W tym przypadku, liczby 2 i 4 są wyrazami skrajnymi, natomiast 3 i 6 są wyrazami środkowymi. Proporcje są niezwykle ważne w matematyce, ponieważ pozwalają na analizę i porównywanie wartości w różnych kontekstach.
Dlaczego obliczanie proporcji jest ważne w codziennym życiu?
Obliczanie proporcji jest niezwykle istotne w codziennym życiu, ponieważ pozwala na podejmowanie świadomych decyzji w różnych sytuacjach. Na przykład, podczas gotowania, proporcje składników muszą być odpowiednio dostosowane, aby uzyskać idealny smak potrawy. Jeśli przepis wymaga 2 filiżanek mąki na 1 filiżankę cukru, a my chcemy przygotować większą porcję, musimy umieć obliczyć, ile mąki potrzebujemy, zachowując odpowiednie proporcje.
W handlu, proporcje są kluczowe dla ustalania cen i rabatów. Na przykład, jeśli produkt kosztuje 100 zł, a sklep oferuje 20% zniżki, musimy obliczyć nową cenę, stosując odpowiednie proporcje. Również w budżetowaniu, proporcje pomagają w planowaniu wydatków, aby nie przekroczyć ustalonego limitu. Zrozumienie, jak działają proporcje, wpływa na naszą zdolność do efektywnego zarządzania czasem i zasobami w życiu codziennym.
Jak rozwiązywać proporcje za pomocą ilorazów i równości?
Rozwiązywanie proporcji w matematyce opiera się na porównywaniu ilorazów i ustawianiu ich w formie równości. Aby rozwiązać proporcję, należy najpierw zrozumieć, że możemy zapisać ją jako a:b = c:d. W tym przypadku, aby znaleźć jedną z wartości, możemy użyć metody krzyżowej, która polega na mnożeniu wyrazów skrajnych i środkowych. Na przykład, jeśli mamy proporcję 3:4 = x:12, możemy pomnożyć 3 przez 12 i 4 przez x, co daje równanie 3 * 12 = 4 * x. Następnie, po obliczeniach, możemy znaleźć wartość x.
Przykłady obliczania proporcji w różnych kontekstach matematycznych
Proporcje znajdują zastosowanie w wielu kontekstach matematycznych, takich jak geometria i algebra. Na przykład, w geometrii możemy użyć proporcji do obliczenia długości boków podobnych figur. Jeśli dwa trójkąty są podobne, to stosunek długości ich boków jest stały. W algebrze, możemy napotkać sytuacje, w których musimy obliczyć wartości zmiennych w równaniach, które zawierają proporcje. Na przykład, w równaniu 5x = 15, możemy użyć proporcji do obliczenia x, co prowadzi nas do rozwiązania x = 3.
| Metoda | Opis |
| Krzyżowe mnożenie | Mnożenie wyrazów skrajnych i środkowych, aby znaleźć brakującą wartość. |
| Ustalanie równości | Ustawienie proporcji jako równości i rozwiązanie równania. |
| Porównanie wartości | Porównywanie wartości w różnych kontekstach matematycznych. |
Zastosowania proporcji w praktyce - przykłady z życia
Proporcje mają wiele praktycznych zastosowań w codziennym życiu, które mogą znacząco ułatwić podejmowanie decyzji. Na przykład, w gotowaniu, często musimy dostosować składniki w przepisach, aby uzyskać odpowiednie smaki i konsystencję potraw. Jeśli przepis na ciasto wymaga 2 filiżanek mąki i 1 filiżanki cukru, a chcemy przygotować dwukrotną porcję, musimy umieć obliczyć, ile mąki i cukru będzie potrzebne, zachowując odpowiednie proporcje. Zrozumienie, jak działa obliczanie proporcji, pozwala uniknąć błędów i zapewnia, że nasze potrawy będą smakować doskonale.
W handlu, proporcje są kluczowe w ustalaniu cen oraz w strategiach rabatowych. Na przykład, jeśli sklep oferuje 30% zniżki na produkt, który kosztuje 200 zł, klienci muszą wiedzieć, jak obliczyć nową cenę, aby ocenić, czy oferta jest korzystna. Proporcje są również używane w marketingu, aby prezentować oferty w sposób, który przyciąga uwagę klientów. Każde z tych zastosowań pokazuje, jak ważne jest zrozumienie i umiejętność obliczania proporcji w praktyce.
Jak proporcje pomagają w rozwiązywaniu problemów w handlu?
W handlu, proporcje odgrywają kluczową rolę w ustalaniu cen oraz w planowaniu strategii rabatowych. Na przykład, jeśli produkt kosztuje 150 zł, a sklep oferuje 20% zniżki, klienci mogą obliczyć, ile zapłacą po zniżce. W tym przypadku, 20% z 150 zł to 30 zł, co oznacza, że nowa cena wynosi 120 zł. Proporcje są również używane do analizy danych sprzedażowych, co pozwala firmom na lepsze dostosowanie swoich ofert do potrzeb klientów. W ten sposób, umiejętność obliczania proporcji jest niezwykle przydatna w codziennych operacjach handlowych.
Proporcje w naukach przyrodniczych - zastosowanie w eksperymentach
W naukach przyrodniczych, proporcje są kluczowe dla przeprowadzania eksperymentów i analizowania wyników. Na przykład, w chemii, podczas przygotowywania roztworów, naukowcy muszą stosować odpowiednie proporcje substancji chemicznych, aby uzyskać pożądane stężenie. Jeśli chcą przygotować 500 ml roztworu z 5% stężeniem, muszą obliczyć, ile mililitrów substancji należy dodać do wody, aby osiągnąć tę proporcję. Podobnie, w biologii, proporcje są używane do obliczania ilości składników odżywczych w hodowlach komórkowych, co jest niezbędne do zapewnienia odpowiednich warunków dla wzrostu komórek.
Czytaj więcej: Do kiedy można zmienić szkołę średnią: terminy i procedura przeniesienia

Wizualizacje i narzędzia wspierające obliczanie proporcji
Wizualizacje i narzędzia graficzne mogą znacząco ułatwić obliczanie proporcji i zrozumienie tego zagadnienia. Wiele osób korzysta z diagramów, wykresów i tabel, aby lepiej zobrazować relacje między różnymi wartościami. Na przykład, wykresy słupkowe mogą pomóc w porównywaniu proporcji różnych składników w przepisach kulinarnych, a diagramy kołowe mogą wizualizować udział poszczególnych elementów w całości. Używanie takich narzędzi pozwala na szybsze i bardziej intuicyjne zrozumienie proporcji oraz ich zastosowania w różnych dziedzinach.Jak korzystać z diagramów i wykresów do obliczania proporcji?
Diagramy i wykresy są doskonałymi narzędziami do wizualizacji proporcji. Na przykład, diagramy kołowe mogą być używane do przedstawienia udziału różnych składników w mieszance, co ułatwia analizę. Aby skutecznie korzystać z tych narzędzi, warto zadbać o ich czytelność i przejrzystość. Wykresy słupkowe mogą z kolei pomóc w porównywaniu proporcji między różnymi grupami danych. Używając tych narzędzi, możemy szybko i efektywnie obliczać oraz zrozumieć proporcje, co jest nieocenione w pracy naukowej i codziennych zadaniach.
| Rodzaj diagramu | Zastosowanie |
| Diagram kołowy | Przedstawienie udziału składników w całości. |
| Wykres słupkowy | Porównanie proporcji różnych grup danych. |
| Wykres liniowy | Analiza zmian proporcji w czasie. |
Jak wykorzystać proporcje w tworzeniu skutecznych strategii marketingowych?
Proporcje mogą być niezwykle przydatne nie tylko w naukach przyrodniczych czy codziennych zadaniach, ale również w tworzeniu strategii marketingowych. Analiza danych sprzedażowych przy użyciu proporcji pozwala na zrozumienie, które produkty są najpopularniejsze wśród klientów oraz jakie są ich preferencje. Na przykład, jeśli 70% klientów wybiera jeden produkt, a 30% inny, marketerzy mogą dostosować swoje kampanie reklamowe, aby skoncentrować się na promowaniu tego, co jest bardziej pożądane. Dzięki temu, efektywność kampanii może wzrosnąć, a zasoby mogą być lepiej alokowane.Dodatkowo, proporcje mogą być używane do analizy efektywności różnych kanałów marketingowych. Na przykład, jeśli kampania w mediach społecznościowych generuje 60% całkowych konwersji, a kampania e-mailowa tylko 20%, zrozumienie tych proporcji pozwala na optymalizację budżetu marketingowego. Marketerzy mogą skoncentrować się na kanałach, które przynoszą najlepsze wyniki, a także testować różne podejścia, aby poprawić wyniki w mniej efektywnych obszarach. W ten sposób, umiejętność obliczania i analizy proporcji staje się kluczowym narzędziem w strategii marketingowej, prowadzącym do lepszych wyników i wyższej rentowności.