Systemy liczenia w matematyce to różnorodne metody zapisu i operacji na liczbach, które są kluczowe w wielu dziedzinach życia codziennego oraz nauki. Najbardziej powszechnym systemem jest system dziesiętny, który opiera się na dziesięciu cyfrach: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9. Jednak istnieje wiele innych systemów, takich jak binarne, ósemkowe czy szesnastkowe, które mają swoje unikalne cechy i zastosowania.
W miarę jak technologia się rozwija, zrozumienie tych systemów staje się coraz bardziej istotne, zwłaszcza w kontekście programowania i obliczeń cyfrowych. W artykule przyjrzymy się różnorodności systemów liczenia, ich zastosowaniom oraz metodom konwersji między nimi, co pozwoli lepiej zrozumieć ich rolę w matematyce i informatyce.
Kluczowe informacje:- System dziesiętny jest najczęściej używany w codziennym życiu i opiera się na dziesięciu cyfrach.
- System binarny, składający się tylko z dwóch cyfr (0 i 1), jest fundamentem działania komputerów.
- System ósemkowy ma zastosowanie w niektórych aplikacjach informatycznych i historycznych kontekstach.
- System szesnastkowy jest istotny w programowaniu, szczególnie w kontekście adresowania pamięci i kolorów w grafice komputerowej.
- Konwersja między systemami liczbowymi jest kluczowa w matematyce i informatyce, a różne algorytmy ułatwiają te procesy.
Różnorodność systemów liczenia w matematyce i ich znaczenie
W matematyce istnieje wiele systemów liczenia, które odgrywają kluczową rolę w zrozumieniu i operowaniu na liczbach. Każdy system ma swoje unikalne cechy i zastosowania, co czyni je niezwykle istotnymi w różnych dziedzinach, od codziennych obliczeń po skomplikowane operacje w informatyce. Zrozumienie tych systemów pozwala na lepsze wykorzystanie narzędzi matematycznych oraz ułatwia pracę w takich obszarach jak programowanie, inżynieria czy nauki przyrodnicze.
Najczęściej spotykanym systemem jest system dziesiętny, który opiera się na dziesięciu cyfrach: 0, 1, 2, 3, 4, 5, 6, 7, 8 i 9. Jednak inne systemy, takie jak binarne, ósemkowe czy szesnastkowe, mają swoje zastosowania, które są równie ważne. Na przykład, system binarny jest podstawą działania komputerów, podczas gdy system szesnastkowy jest często używany w programowaniu i grafice komputerowej. Zrozumienie różnorodności systemów liczenia w matematyce jest kluczowe dla każdego, kto chce w pełni wykorzystać potencjał matematyki w praktyce.
Zrozumienie systemu dziesiętnego i jego zastosowanie
System dziesiętny, znany również jako system dziesiętny, jest najpopularniejszym systemem liczbowym, z którym spotykamy się na co dzień. Opiera się na dziesięciu cyfrach, co sprawia, że jest intuicyjny i łatwy do zrozumienia. W tym systemie każda cyfra ma swoją wartość w zależności od miejsca, w którym się znajduje, co oznacza, że liczba 345 jest interpretowana jako 3 setki, 4 dziesiątki i 5 jedności. Dzięki tej strukturze możemy łatwo wykonywać podstawowe operacje matematyczne, takie jak dodawanie, odejmowanie, mnożenie i dzielenie.
W codziennym życiu system dziesiętny ma wiele zastosowań. Używamy go do mierzenia czasu, pieniędzy, odległości i wielu innych rzeczy. Na przykład, ceny produktów w sklepach są podawane w systemie dziesiętnym, co ułatwia zakupy i porównywanie wartości. Również w edukacji, system dziesiętny jest podstawą nauczania matematyki, co sprawia, że jego zrozumienie jest niezbędne dla każdego ucznia.
Cechy systemu binarnego i jego rola w informatyce
System binarny, znany również jako system dwójkowy, jest fundamentalnym systemem liczbowym, który opiera się na dwóch cyfrach: 0 i 1. W przeciwieństwie do systemu dziesiętnego, który używa dziesięciu cyfr, system binarny jest niezwykle prosty, co czyni go idealnym do reprezentacji danych w komputerach. Każda cyfra w systemie binarnym nazywana jest bit, a osiem bitów tworzy bajt, co jest podstawową jednostką danych w informatyce.
Rola systemu binarnego w informatyce jest nie do przecenienia. Komputery operują na danych w postaci binarnej, co oznacza, że wszystkie operacje, od prostych obliczeń po złożone algorytmy, są wykonywane w tym systemie. Dzięki binarnym reprezentacjom możliwe jest przechowywanie i przetwarzanie informacji w sposób efektywny i niezawodny. Na przykład, wszystkie programy komputerowe, aplikacje oraz systemy operacyjne wykorzystują binarność do działania, co czyni go kluczowym elementem współczesnej technologii.
Porównanie systemów liczbowych: co je różni i łączy
W matematyce istnieje wiele różnych systemów liczbowych, z których każdy ma swoje unikalne cechy i zastosowania. System binarny, ósemkowy i szesnastkowy różnią się głównie podstawą, na której są oparte. Na przykład, system binarny używa tylko dwóch cyfr, podczas gdy system ósemkowy korzysta z ośmiu, a system szesnastkowy z szesnastu. Mimo tych różnic, wszystkie te systemy mają wspólny cel: umożliwiają reprezentację liczb i operacji matematycznych w różnych kontekstach.
Porównując te systemy, można zauważyć, że każdy z nich ma swoje zastosowanie w różnych dziedzinach. Na przykład, system binarny jest kluczowy w informatyce, podczas gdy system szesnastkowy jest często używany w programowaniu i grafice komputerowej. Zrozumienie tych różnic i podobieństw jest istotne dla każdego, kto chce w pełni zrozumieć systemy liczenia w matematyce.
| System | Podstawa | Cyfry | Zastosowanie |
| Binarny | 2 | 0, 1 | Komputery, programowanie |
| Ósemkowy | 8 | 0, 1, 2, 3, 4, 5, 6, 7 | Niektóre systemy informatyczne |
| Szesnastkowy | 16 | 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F | Programowanie, grafika komputerowa |
System ósemkowy: historia i zastosowania w praktyce
System ósemkowy, znany również jako system ośmiu, ma swoje korzenie w starożytności, kiedy to był używany przez różne cywilizacje, w tym Babilończyków. Jego popularność wynikała z faktu, że ludzie często posługiwali się grupami ośmiu, co czyniło go naturalnym wyborem do codziennych obliczeń. Współczesne zastosowanie systemu ósemkowego jest mniej powszechne niż w przeszłości, ale nadal znajduje swoje miejsce w niektórych dziedzinach, zwłaszcza w informatyce.
Obecnie system ósemkowy ma zastosowanie w programowaniu oraz w niektórych systemach informatycznych, gdzie umożliwia efektywne reprezentowanie danych. Na przykład, w niektórych systemach operacyjnych i aplikacjach, takich jak Unix, numery ósemkowe są używane do oznaczania uprawnień plików. Dzięki swojej prostocie, system ósemkowy może być także wykorzystywany w edukacji do nauczania podstaw konwersji między różnymi systemami liczbowymi.
System szesnastkowy: dlaczego jest ważny w programowaniu
System szesnastkowy, znany również jako system heksadecymalny, jest niezwykle istotny w świecie programowania i informatyki. Używa szesnastu cyfr: 0-9 oraz A-F, gdzie A reprezentuje 10, B 11, C 12, D 13, E 14, a F 15. Jego główną zaletą jest to, że pozwala na bardziej zwięzłe przedstawienie dużych liczb binarnych, co jest szczególnie przydatne w kontekście adresowania pamięci oraz reprezentacji kolorów w grafice komputerowej.
W praktyce, system szesnastkowy jest powszechnie stosowany w programowaniu, na przykład w języku Java czy C++, gdzie kolory są definiowane za pomocą wartości heksadecymalnych. Przykładowo, kolor biały w systemie szesnastkowym to #FFFFFF, co oznacza maksymalne wartości dla czerwonego, zielonego i niebieskiego. Dzięki temu programiści mogą łatwo manipulować kolorami w aplikacjach graficznych i stronach internetowych. System szesnastkowy jest również używany w debugowaniu, gdzie wartości pamięci są często przedstawiane w formie heksadecymalnej, co ułatwia analizę i zrozumienie danych.
Czytaj więcej: Branżowa szkoła 2 stopnia - jak się dostać i co warto wiedzieć

Jak konwertować liczby między różnymi systemami liczbowymi
Konwersja między różnymi systemami liczbowymi jest kluczowym aspektem matematyki i informatyki. Dzięki umiejętności przekształcania liczb z jednego systemu do innego, możemy lepiej zrozumieć, jak działają różne systemy liczenia i jak są używane w praktyce. W szczególności konwersje między systemem dziesiętnym a binarnym są niezwykle ważne, ponieważ stanowią podstawę działania komputerów i większości nowoczesnych technologii. Istnieje wiele metod konwersji, które mogą być stosowane w różnych sytuacjach, w zależności od potrzeb użytkownika.
W praktyce, konwersja może być przeprowadzana na kilka sposobów, w tym poprzez algorytmy, które automatyzują procesy przekształcania liczb. Dzięki tym metodom, programiści i matematycy mogą szybko i efektywnie przekształcać liczby, co jest niezbędne w wielu dziedzinach, takich jak programowanie, inżynieria czy analiza danych. W kolejnych sekcjach przedstawimy konkretne przykłady konwersji oraz zastosowanie algorytmów do tego celu.
- Konwersja z systemu dziesiętnego na binarny przy użyciu metody dzielenia przez 2.
- Przykłady konwersji z systemu binarnego na dziesiętny przez sumowanie wartości pozycji.
- Użycie narzędzi online do szybkości konwersji między systemami liczbowymi.
Przykłady konwersji z systemu dziesiętnego na binarny
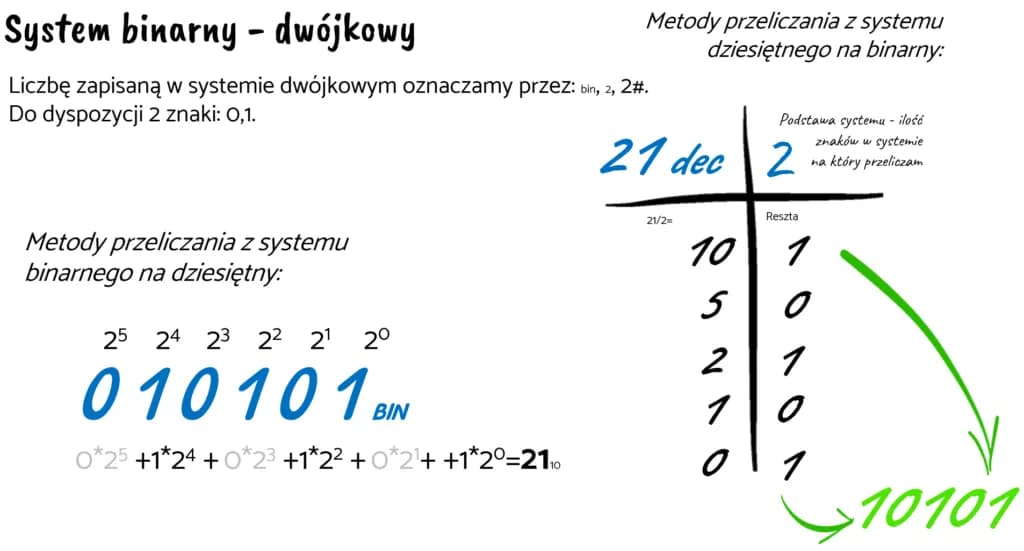
Konwersja liczb z systemu dziesiętnego na system binarny polega na przekształceniu wartości dziesiętnej do postaci, w której używane są tylko cyfry 0 i 1. Proces ten można przeprowadzić na kilka sposobów, ale jedną z najprostszych metod jest metoda dzielenia przez 2. W tej metodzie dzielimy liczbę dziesiętną przez 2, zapisując reszty z każdego dzielenia, aż osiągniemy wynik 0. Następnie odczytujemy reszty w odwrotnej kolejności, co daje nam wynik w systemie binarnym.Na przykład, aby przekonwertować liczbę 13 na system binarny, dzielimy ją przez 2:
- 13 ÷ 2 = 6, reszta 1
- 6 ÷ 2 = 3, reszta 0
- 3 ÷ 2 = 1, reszta 1
- 1 ÷ 2 = 0, reszta 1
Zastosowanie algorytmów do konwersji między systemami
W konwersji między różnymi systemami liczbowymi, takich jak dziesiętny, binarny, ósemkowy czy szesnastkowy, wykorzystuje się różne algorytmy. Najpopularniejsze z nich to algorytm dzielenia i algorytm mnożenia. Algorytm dzielenia, który opisaliśmy wcześniej, jest szczególnie efektywny w konwersji z systemu dziesiętnego na binarny, podczas gdy algorytm mnożenia jest często używany do konwersji z binarnego na dziesiętny.
Na przykład, aby przekonwertować liczbę binarną 1011 na system dziesiętny, należy pomnożyć każdą cyfrę przez odpowiednią potęgę liczby 2:
- 1 × 2³ = 8
- 0 × 2² = 0
- 1 × 2¹ = 2
- 1 × 2⁰ = 1
Jak systemy liczenia wpływają na rozwój sztucznej inteligencji
W miarę jak technologia rozwija się, a sztuczna inteligencja (AI) staje się coraz bardziej powszechna, zrozumienie różnych systemów liczenia nabiera nowego znaczenia. AI opiera się na algorytmach, które przetwarzają dane w formatach binarnych, a także wykorzystują systemy szesnastkowe i ósemkowe do efektywnego zarządzania dużymi zbiorami danych. Umiejętność konwersji między tymi systemami jest kluczowa dla programistów i inżynierów, którzy tworzą modele AI, umożliwiając im optymalizację algorytmów oraz poprawę wydajności obliczeń.
W przyszłości, rozwój technologii obliczeniowych, takich jak kwantowe komputery, może zrewolucjonizować sposób, w jaki przetwarzamy informacje w różnych systemach liczbowych. Komputery kwantowe operują na qubitach, które mogą reprezentować więcej niż jedną wartość jednocześnie, co stwarza nowe możliwości dla algorytmów konwersji. Zrozumienie, jak różne systemy liczenia współdziałają z nowymi technologiami, może pomóc w opracowywaniu bardziej zaawansowanych aplikacji AI, które będą w stanie rozwiązywać złożone problemy w czasie rzeczywistym.