W matematyce znaki mniejszości i większości odgrywają kluczową rolę w porównywaniu liczb. Znak mniejszości ("<") oznacza, że liczba po lewej stronie jest mniejsza od liczby po prawej stronie, na przykład 2 < 5. Z kolei znak większości (">") wskazuje, że liczba po lewej stronie jest większa od liczby po prawej stronie, na przykład 5 > 2. Zrozumienie tych symboli jest niezbędne do wykonywania wielu operacji matematycznych, a także do analizy danych.
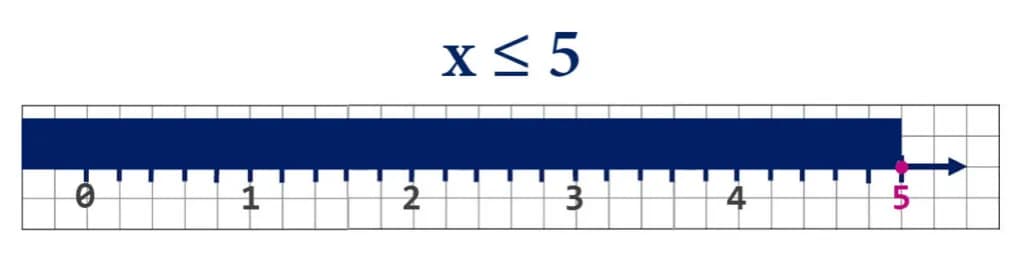
W artykule przyjrzymy się bliżej tym znakom, ich zastosowaniom oraz typowym błędom, jakie mogą występować podczas ich użycia. Dzięki temu będziesz mógł lepiej zrozumieć, jak poprawnie porównywać liczby i unikać powszechnych nieporozumień związanych z tymi symbolami.
Kluczowe informacje:- Znak mniejszości "<" oznacza, że liczba po lewej stronie jest mniejsza od liczby po prawej stronie.
- Znak większości ">" wskazuje, że liczba po lewej stronie jest większa od liczby po prawej stronie.
- Znaki te są używane do porównywania zarówno liczb całkowitych, jak i ułamkowych.
- Wizualizacje, takie jak diagramy, mogą ułatwić zrozumienie tych symboli.
- Typowe błędy obejmują mylenie znaków mniejszości i większości, co prowadzi do nieprawidłowych porównań.
Znaki mniejszości i większości w matematyce - co oznaczają?
W matematyce znaki mniejszości i większości są niezbędne do porównywania liczb. Znak mniejszości "<" wskazuje, że liczba po lewej stronie jest mniejsza od liczby po prawej stronie, na przykład 2 < 5. Z kolei znak większości ">" oznacza, że liczba po lewej stronie jest większa od liczby po prawej stronie, na przykład 5 > 2. Te symbole są kluczowe w wielu operacjach matematycznych, ponieważ pozwalają na łatwe i szybkie porównania między różnymi wartościami.
Znaki te są szeroko stosowane w różnych dziedzinach matematyki, od podstawowych działań arytmetycznych po bardziej zaawansowane analizy statystyczne. Ich zrozumienie jest istotne nie tylko dla uczniów, ale także dla każdego, kto chce skutecznie pracować z danymi liczbowymi. Umiejętność poprawnego użycia tych symboli pozwala unikać błędów w obliczeniach i interpretacjach wyników.
Znak mniejszości "
Znak mniejszości "<" jest symbolem używanym w matematyce do wskazywania, że jedna liczba jest mniejsza od drugiej. Na przykład, w wyrażeniu 3 < 5, liczba 3 jest mniejsza od liczby 5. Ten symbol jest kluczowy w porównaniach, ponieważ pozwala na szybkie określenie relacji między dwiema wartościami. W praktyce, znak mniejszości jest często wykorzystywany w matematyce, statystyce oraz w codziennych obliczeniach.
Przykłady użycia znaku mniejszości "<" można znaleźć w różnych kontekstach. Na przykład, w analizie danych, można porównywać wyniki testów, aby zobaczyć, które z nich są niższe. W przypadku pomiarów, można stwierdzić, że temperatura 15°C < 20°C, co oznacza, że 15°C jest niższa od 20°C. Tego rodzaju porównania są powszechne i pomagają w lepszym zrozumieniu relacji między danymi.
- 5 < 10 - liczba 5 jest mniejsza od 10.
- 2.5 < 3.7 - wartość 2.5 jest mniejsza od 3.7.
- -1 < 0 - liczba -1 jest mniejsza od 0.
- 100 < 150 - liczba 100 jest mniejsza od 150.
- 3 < 4.5 - liczba 3 jest mniejsza od 4.5.
Czytaj więcej: Punkty edukacyjne jak i za ile: poznaj wartości i wymagania szkoleń
Znak większości ">" - jak go rozumieć i stosować
Znak większości ">" jest symbolem, który wskazuje, że jedna liczba jest większa od drugiej. Na przykład, w wyrażeniu 7 > 4, liczba 7 jest większa od liczby 4. Ten symbol jest niezwykle ważny w matematyce, ponieważ pozwala na szybkie porównanie wartości i zrozumienie ich relacji. Znak większości jest używany w różnych kontekstach, od prostych obliczeń po bardziej złożone analizy danych.
W praktyce, znak ">" znajduje zastosowanie w wielu dziedzinach, takich jak statystyka, ekonomia czy nauki przyrodnicze. Na przykład, w badaniach naukowych można stwierdzić, że wynik testu 85 > 75 oznacza, że wynik 85 jest lepszy od 75. Takie porównania są powszechne i pomagają w podejmowaniu decyzji na podstawie danych liczbowych.
- 8 > 5 - liczba 8 jest większa od 5.
- 15.2 > 10.1 - wartość 15.2 jest większa od 10.1.
- 0 > -3 - liczba 0 jest większa od -3.
- 200 > 150 - liczba 200 jest większa od 150.
- 4.5 > 3 - liczba 4.5 jest większa od 3.
Przykłady porównań liczbowych z użyciem znaków
Porównania liczb całkowitych z użyciem znaków mniejszości i większości są powszechnie stosowane w matematyce. Na przykład, możemy porównywać liczby takie jak 10 i 20, stwierdzając, że 10 < 20, co oznacza, że liczba 10 jest mniejsza od 20. Takie porównania są nie tylko istotne w zadaniach matematycznych, ale również w codziennym życiu, na przykład przy ocenie wyników testów czy analizie danych finansowych. Zrozumienie tych relacji pozwala na lepsze podejmowanie decyzji opartych na liczbach.
W przypadku liczb ułamkowych, porównania również odgrywają kluczową rolę. Na przykład, 1/2 < 3/4, co oznacza, że połowa jest mniejsza od trzech czwartych. Takie porównania pomagają w zrozumieniu wielkości ułamków i ich zastosowania w różnych kontekstach, na przykład w kuchni przy gotowaniu czy w naukach przyrodniczych. Warto zauważyć, że porównania ułamków mogą być nieco bardziej skomplikowane, ale zasady pozostają takie same.
| Typ liczby | Przykład 1 | Przykład 2 |
|---|---|---|
| Całkowite | 5 < 10 | 15 > 7 |
| Ułamkowe | 1/3 < 1/2 | 2/5 > 1/4 |
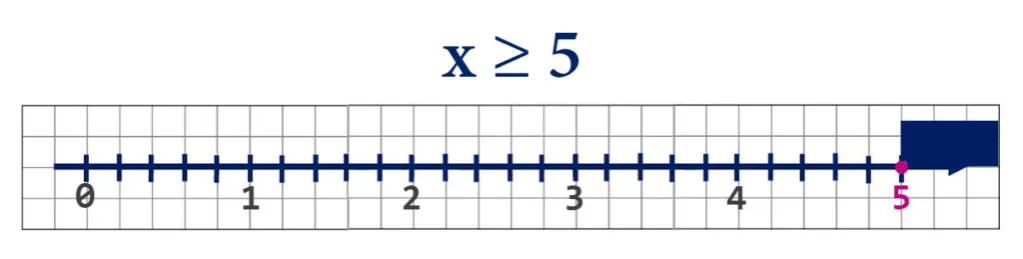
Wizualizacje znaków mniejszości i większości w matematyce
Wizualizacje są kluczowym narzędziem w zrozumieniu znaków mniejszości i większości w matematyce. Pomagają one w łatwiejszym przyswojeniu koncepcji porównywania liczb, umożliwiając lepsze zrozumienie relacji między wartościami. Diagramy i ilustracje mogą pokazywać, jak symbole "<" i ">" działają w praktyce, co sprawia, że nauka staje się bardziej przystępna i atrakcyjna. Dzięki wizualizacjom uczniowie mogą szybko zobaczyć, które liczby są większe lub mniejsze, co wspiera ich zdolności analityczne.
Na przykład, diagramy mogą przedstawiać liczby na osi liczbowej, gdzie można łatwo zobaczyć, która z nich jest większa, a która mniejsza. Dodatkowo, użycie kolorów lub symboli graficznych może jeszcze bardziej ułatwić zrozumienie tych pojęć. Takie wizualizacje są szczególnie przydatne w edukacji, ponieważ angażują różne zmysły ucznia, co sprzyja lepszemu zapamiętywaniu i zrozumieniu materiału.
| Typ wizualizacji | Opis |
|---|---|
| Oś liczbową | Pokazuje liczby w porządku rosnącym, ilustrując relacje między nimi. |
| Wykresy słupkowe | Umożliwiają porównanie różnych wartości, wizualizując, która liczba jest większa. |
| Diagramy Venn'a | Pomagają zrozumieć relacje między zbiorami, pokazując, które liczby są wspólne. |
Praktyczne zastosowania znaków mniejszości i większości w życiu codziennym
Znaki mniejszości i większości znajdują zastosowanie nie tylko w matematyce, ale również w codziennym życiu, zwłaszcza w podejmowaniu decyzji opartych na danych. Na przykład, w analizie finansowej, umiejętność porównywania wydatków i przychodów przy użyciu symboli "<" i ">" pozwala na lepsze zarządzanie budżetem. Klienci mogą szybko ocenić, które opcje zakupowe są korzystniejsze, porównując ceny produktów i usługi, co prowadzi do bardziej świadomych wyborów.
W kontekście technologii, znaki te są również wykorzystywane w programowaniu i analizie danych. Programiści używają symboli mniejszości i większości w kodzie, aby tworzyć warunki logiczne, które decydują o dalszym przebiegu działania programów. W przyszłości, z rosnącą rolą sztucznej inteligencji i analizy danych, umiejętność wykorzystania tych znaków w bardziej zaawansowanych algorytmach stanie się jeszcze bardziej istotna, otwierając nowe możliwości w różnych dziedzinach, takich jak big data czy uczenie maszynowe.
