Mianownik jest kluczowym pojęciem w matematyce, które odnosi się do liczby znajdującej się pod kreską ułamkową w ułamku. Zrozumienie tej definicji jest niezbędne do efektywnego posługiwania się ułamkami oraz przeprowadzania różnych operacji matematycznych. Bez znajomości roli mianownika, trudniej jest zrozumieć, jak działają ułamki, co może prowadzić do błędów w obliczeniach.
W tym artykule przyjrzymy się, czym dokładnie jest mianownik, jak go zidentyfikować w różnych rodzajach ułamków oraz jakie ma znaczenie w operacjach matematycznych. Dowiemy się również, jak mianownik wpływa na dodawanie, odejmowanie, mnożenie i dzielenie ułamków. Dzięki temu zyskasz lepsze zrozumienie tego fundamentalnego elementu matematyki.
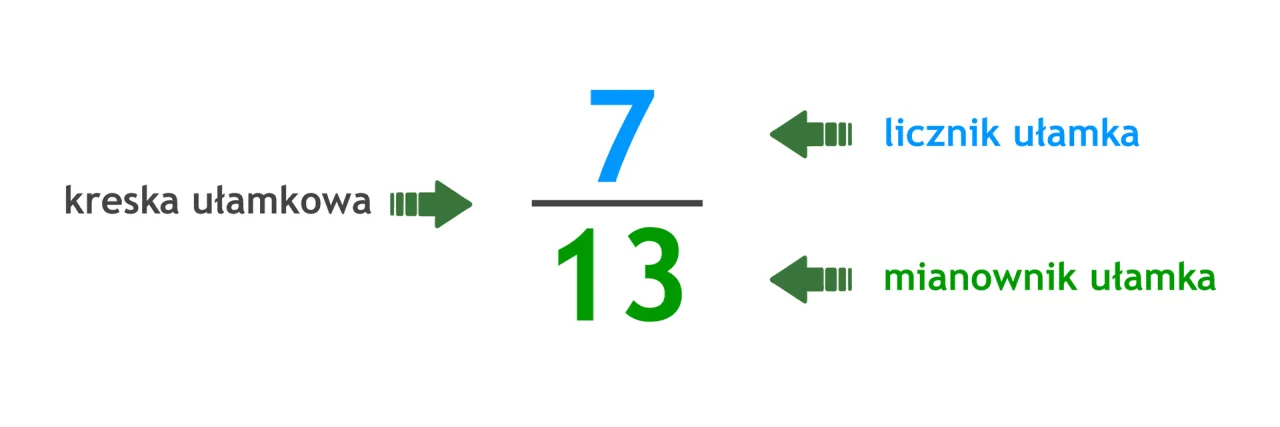
Kluczowe informacje:- Mianownik to liczba znajdująca się pod kreską ułamkową w ułamku.
- Rola mianownika jest kluczowa w zrozumieniu, jak działają ułamki.
- Istnieją różne rodzaje ułamków, w tym ułamki właściwe, niewłaściwe i mieszane.
- Mianownik wpływa na sposób dodawania i odejmowania ułamków, szczególnie w przypadku różnych mianowników.
- W matematyce, zrozumienie mianownika jest niezbędne do poprawnego wykonywania operacji mnożenia i dzielenia ułamków.
- Wizualizacje, takie jak diagramy i wykresy, mogą znacznie ułatwić naukę o mianowniku.
Definicja mianownika i jego podstawowe znaczenie w matematyce
Mianownik jest kluczowym elementem w matematyce, szczególnie w kontekście ułamków. To liczba znajdująca się pod kreską ułamkową, która wskazuje, na ile części dzielimy całość. Zrozumienie, czym jest mianownik, jest niezbędne do poprawnego posługiwania się ułamkami, ponieważ jego wartość wpływa na interpretację i obliczenia z nimi związane.
W matematyce, mianownik pełni fundamentalną rolę w określaniu proporcji i relacji między różnymi wartościami. Bez znajomości tej definicji, trudno jest w pełni zrozumieć, jak działają ułamki i jakie mają zastosowanie w różnych obliczeniach. Dlatego znajomość mianownika jest kluczowa dla każdego, kto chce skutecznie uczyć się matematyki.Mianownik w kontekście ułamków – co to oznacza?
Mianownik w ułamku ma szczególne znaczenie, ponieważ określa, na ile równych części dzielimy całość. Na przykład w ułamku ¾, liczba 4 jest mianownikiem, co oznacza, że całość została podzielona na 4 równe części, z których 3 są brane pod uwagę. Dzięki temu możemy zrozumieć, jak ułamki reprezentują różne wartości w kontekście dzielenia.
Warto zauważyć, że mianownik nie tylko określa liczbę części, ale także wpływa na to, jak porównujemy różne ułamki. Ułatwia to zrozumienie, jak różne wartości mogą być ze sobą związane i jakie mają proporcje. W matematyce, znajomość roli mianownika jest kluczowa w analizie i interpretacji danych.
Jak zidentyfikować mianownik w różnych rodzajach ułamków?
Aby zidentyfikować mianownik w różnych rodzajach ułamków, najpierw musimy zrozumieć, że mianownik jest zawsze umieszczony pod kreską ułamkową. W matematyce wyróżniamy kilka typów ułamków, w tym ułamki właściwe, niewłaściwe oraz mieszane. Każdy z tych typów ma swoje specyficzne cechy, ale zasada identyfikacji mianownika pozostaje ta sama.
W ułamku właściwym, takim jak ⅗, mianownik to 5, co oznacza, że całość jest podzielona na 5 równych części. W przypadku ułamków niewłaściwych, na przykład 7/4, również możemy zauważyć, że mianownik wynosi 4. Ułamki mieszane, takie jak 2 ½, wymagają dodatkowego kroku, aby znaleźć mianownik, który w tym przypadku wynosi 2, ponieważ jest to ułamek ½.
Jak mianownik wpływa na dodawanie i odejmowanie ułamków?
Mianownik odgrywa kluczową rolę w procesie dodawania i odejmowania ułamków. Aby dodać lub odjąć ułamki, musimy upewnić się, że mają one ten sam mianownik. Kiedy ułamki mają różne mianowniki, należy je najpierw sprowadzić do wspólnego mianownika, co pozwala na łatwiejsze przeprowadzenie obliczeń. Bez tego kroku, wyniki mogą być błędne i wprowadzać w błąd.
Na przykład, w przypadku dodawania ułamków ⅓ i ¼, najpierw musimy znaleźć wspólny mianownik, którym w tym przypadku będzie 12. Po przekształceniu ułamków na 4/12 i 3/12, możemy je dodać, co daje 7/12. Podobna zasada obowiązuje przy odejmowaniu ułamków, gdzie również musimy mieć wspólny mianownik, aby poprawnie wykonać operację.
- Znajdź wspólny mianownik dla ułamków, które chcesz dodać lub odjąć.
- Przekształć ułamki, aby miały ten sam mianownik.
- Wykonaj dodawanie lub odejmowanie licznika, zachowując mianownik.
- Jeśli to możliwe, uprość wynikowy ułamek.
Znaczenie mianownika w mnożeniu i dzieleniu ułamków
Mianownik również ma istotne znaczenie w mnożeniu i dzieleniu ułamków. W przeciwieństwie do dodawania i odejmowania, w przypadku mnożenia ułamków, nie musimy sprowadzać ich do wspólnego mianownika. Zamiast tego, wystarczy pomnożyć liczniki przez siebie i mianowniki przez siebie. Na przykład, w przypadku mnożenia ⅓ przez ¼, wynik to ⅓ × ¼ = ⅑.
W przypadku dzielenia ułamków, proces jest podobny, ale wymaga zastosowania odwrotności mianownika. Aby podzielić ⅓ przez ¼, należy pomnożyć ⅓ przez odwrotność ¼, co daje ⅓ × 4/1 = 4/3. Dzięki temu, zrozumienie roli mianownika w tych operacjach jest kluczowe dla poprawnych obliczeń.
Przykłady ułamków z różnymi mianownikami dla lepszego zrozumienia
Przykłady ułamków są niezwykle ważne dla zrozumienia, jak działają różne mianowniki. Umożliwiają one wizualizację tego, jak ułamki z różnymi mianownikami mogą być porównywane i przekształcane. Przykłady pomagają również w nauce dodawania, odejmowania, mnożenia i dzielenia ułamków, co jest kluczowe w matematyce. Dzięki nim można zobaczyć, jak zmieniają się wartości ułamków w zależności od mianownika, co ułatwia zrozumienie tego pojęcia.
Na przykład, rozważmy ułamki ⅓, ½ i ¼. Każdy z nich ma inny mianownik, co wpływa na ich wartość i sposób, w jaki można je ze sobą porównywać. W przypadku dodawania tych ułamków, konieczne będzie znalezienie wspólnego mianownika, co pokazuje, jak ważne jest zrozumienie tych podstawowych koncepcji.Analiza ułamków z wspólnym mianownikiem – jak to działa?
Wspólny mianownik to kluczowy koncept, który ułatwia dodawanie i odejmowanie ułamków. Kiedy ułamki mają ten sam mianownik, możemy po prostu dodać lub odjąć ich liczniki, zachowując ten sam mianownik w wyniku. Na przykład, w przypadku ułamków ⅓ i ⅓, ponieważ mają ten sam mianownik, możemy je dodać, co daje ⅔. To sprawia, że operacje są znacznie prostsze i bardziej intuicyjne.| Ułamek 1 | Ułamek 2 | Wynik (po dodaniu) |
|---|---|---|
| ⅓ | ⅓ | ⅔ |
| ¼ | ¼ | ½ |
| ⅖ | ⅖ | ⅗ |
Ułamki o różnych mianownikach – co warto wiedzieć?
Praca z ułamkami o różnych mianownikach może być wyzwaniem, ale zrozumienie tego zagadnienia jest kluczowe w matematyce. Kiedy mamy do czynienia z ułamkami, które mają różne mianowniki, musimy znaleźć sposób na ich porównanie lub wykonanie operacji matematycznych. W takim przypadku najważniejszym krokiem jest znalezienie wspólnego mianownika, który pozwala na uproszczenie obliczeń.
Jednym z najczęstszych problemów, które napotykają uczniowie, jest dodawanie lub odejmowanie ułamków o różnych mianownikach. Aby to zrobić, należy najpierw przekształcić te ułamki, aby miały ten sam mianownik. Można to osiągnąć, znajdując najmniejszy wspólny wielokrotność (NWW) mianowników. Ułatwia to dodawanie i odejmowanie, ponieważ umożliwia operację na licznikach, zachowując ten sam mianownik.
- Ustal mianowniki ułamków, które chcesz porównać lub z którymi chcesz pracować.
- Znajdź najmniejszy wspólny wielokrotność (NWW) dla tych mianowników.
- Przekształć każdy ułamek, aby miał ten sam mianownik, dostosowując liczniki.
- Wykonaj operacje matematyczne na licznikach, zachowując wspólny mianownik.
Czytaj więcej: Edukacja na Węgrzech: co warto wiedzieć o systemie szkolnictwa
Jak zastosować ułamki w codziennym życiu i nauce
Ułamki mają wiele praktycznych zastosowań w codziennym życiu, a zrozumienie ich funkcji może znacząco ułatwić wiele zadań. Na przykład, w kuchni często korzystamy z ułamków podczas gotowania, gdy musimy przeliczać składniki z jednej jednostki miary na inną. Umiejętność szybkiego przekształcania ułamków, takich jak ⅓ szklanki na ¼ szklanki, może pomóc w precyzyjnym odmierzaniu i unikaniu błędów w przepisach.
W kontekście nauki, ułamki są również niezbędne w wielu dziedzinach, takich jak chemia czy fizyka, gdzie często obliczamy proporcje substancji lub analizujemy wyniki eksperymentów. Warto zainwestować czas w ćwiczenie umiejętności pracy z ułamkami, aby stały się one intuicyjne, co ułatwi zarówno codzienne zadania, jak i bardziej zaawansowane obliczenia w przyszłej edukacji czy karierze zawodowej.





