Obliczanie tangensa kąta jest kluczowym zagadnieniem w matematyce, szczególnie w dziedzinie trigonometrii. Tangens, oznaczany jako tan, jest stosunkiem sinusa do cosinusa danego kąta. Dzięki temu, znając wartości sinusa i cosinusa, możemy łatwo obliczyć tangens. W tym artykule przedstawimy proste metody obliczania tangensa oraz podamy praktyczne przykłady dla różnych kątów.
W miarę zgłębiania tematu, omówimy również graficzną interpretację funkcji tangens oraz jej zastosowania w codziennym życiu. Zrozumienie tangensa nie tylko ułatwia rozwiązywanie problemów matematycznych, ale także pozwala na lepsze zrozumienie zjawisk w geometrii i innych dziedzinach nauki.
Kluczowe informacje:- Tangens kąta oblicza się za pomocą wzoru: tan α = sin α / cos α.
- Wartości tangensa można łatwo wyznaczyć, znając wartości sinusa i cosinusa.
- Przykłady obliczeń tangensa dla kątów 0°, 30°, 45°, 60° i 90° są istotne dla zrozumienia tematu.
- Graficzna interpretacja tangensa pokazuje, jak funkcja zachowuje się w różnych zakresach kątów.
- Tangens ma praktyczne zastosowanie w rozwiązywaniu problemów geometrycznych i w różnych dziedzinach nauki.
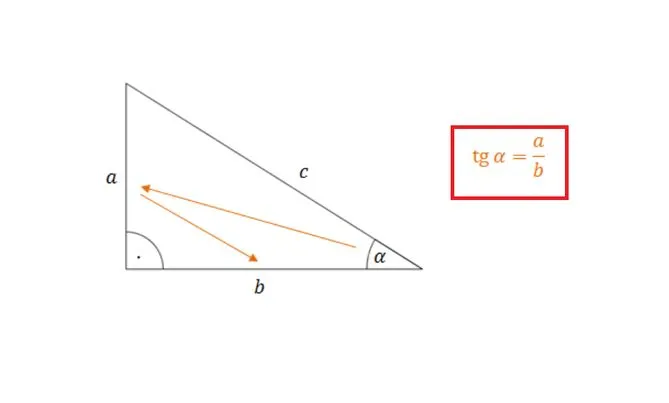
Jak obliczyć tangens kąta: podstawowy wzór i definicja
Tangens kąta, oznaczany jako tan, jest jednym z podstawowych pojęć w trigonometrii. Definiuje się go jako stosunek długości przeciwległej do kąta do długości przyległej w trójkącie prostokątnym. Można go obliczyć za pomocą wzoru: tan α = sin α / cos α, gdzie sin α to sinus kąta, a cos α to cosinus kąta. Dzięki temu wzorowi, znając wartości sinusa i cosinusa, łatwo wyznaczymy tangens dla dowolnego kąta.
Warto zaznaczyć, że tangens ma swoje zastosowanie nie tylko w matematyce, ale także w fizyce i inżynierii. Jest to funkcja okresowa, co oznacza, że powtarza swoje wartości w regularnych odstępach. W praktyce, tangens jest szczególnie użyteczny w obliczeniach związanych z kątami i długościami w trójkątach, a także w analizie wykresów funkcji. Zrozumienie tangensa jest zatem kluczowe dla dalszego zgłębiania tematów związanych z trygonometrią.
Co to jest tangens i jak go zdefiniować w trigonometrii?
Tangens jest funkcją trygonometryczną, która odgrywa istotną rolę w analizie kątów w trójkątach prostokątnych. Jego główną cechą jest to, że można go zdefiniować nie tylko w kontekście trójkątów, ale również za pomocą jednostkowej okrągłej. W jednostkowym okręgu, tangens kąta odpowiada współrzędnej y punktu na okręgu podzielonej przez współrzędną x tego samego punktu. To sprawia, że tangens jest niezwykle przydatny w różnych dziedzinach matematyki i nauki.
W kontekście funkcji trygonometrycznych, tangens jest powiązany z innymi funkcjami, takimi jak sinus i cosinus. Wartości tangensa zmieniają się w zależności od kąta, co prowadzi do jego okresowości. Na przykład, tangens kąta 90° jest nieokreślony, ponieważ cosinus tego kąta wynosi 0. Zrozumienie tych powiązań jest kluczowe dla efektywnego wykorzystania tangensa w obliczeniach matematycznych.
Prosta metoda obliczania tangensa: krok po kroku
Aby obliczyć tangens kąta, można zastosować prostą metodę, która opiera się na wartościach sinusa i cosinusa. Wzór na tangens jest następujący: tan α = sin α / cos α. W tym przypadku, wystarczy znać wartości sinusa i cosinusa dla danego kąta, aby móc wyznaczyć jego tangens. Proces ten jest szybki i efektywny, co czyni go bardzo praktycznym w obliczeniach matematycznych.
W praktyce, aby obliczyć tangens, należy najpierw ustalić kąt, dla którego chcemy znaleźć tangens. Następnie, korzystając z tabeli wartości trygonometrycznych lub kalkulatora, można łatwo odczytać wartości sinusa i cosinusa. Po uzyskaniu tych wartości, wystarczy podzielić sinus przez cosinus, aby uzyskać wynik. Ten prosty proces pozwala na szybkie obliczenia w różnych kontekstach matematycznych.
Jak wykorzystać sinus i cosinus do obliczenia tangensa?
Obliczanie tangensa za pomocą sinusa i cosinusa jest bardzo intuicyjne. Sinus to stosunek długości przeciwległej do kąta w trójkącie prostokątnym, natomiast cosinus to stosunek długości przyległej. Dzięki tym wartościom, możemy łatwo obliczyć tangens, który jest stosunkiem tych dwóch funkcji. Warto zauważyć, że tangens jest również funkcją okresową, co oznacza, że jego wartości powtarzają się w regularnych odstępach.
- Wartości sinusa i cosinusa można znaleźć w tabelach lub obliczyć za pomocą kalkulatorów trygonometrycznych.
- Obliczając tangens, pamiętaj, że tan α = sin α / cos α.
- Znajomość wartości dla podstawowych kątów (0°, 30°, 45°, 60°, 90°) znacznie ułatwia obliczenia.
Czytaj więcej: Nierówności społeczne w Polsce: skala problemu i skutki
Przykłady obliczeń tangensa dla różnych kątów: praktyczne zastosowanie
Obliczanie tangensa dla różnych kątów jest kluczowym elementem w trygonometrii. W tej sekcji przedstawimy konkretne przykłady obliczeń tangensa dla kątów: 0°, 30°, 45°, 60° i 90°. Zrozumienie wartości tangensa dla tych kątów pomoże w lepszym opanowaniu tej funkcji oraz jej zastosowań w praktycznych problemach matematycznych.
| Kąt (°) | Wartość tangensa |
|---|---|
| 0° | 0 |
| 30° | √3/3 (około 0.577) |
| 45° | 1 |
| 60° | √3 (około 1.732) |
| 90° | nieokreślony |
Tangens kątów szczególnych: 0°, 30°, 45°, 60° i 90°
Dla kąta 0°, tangens wynosi 0, ponieważ sinus kąta 0° to 0, a cosinus to 1. W przypadku kąta 30°, tangens wynosi √3/3, co oznacza, że stosunek długości przeciwległej do przyległej w trójkącie prostokątnym jest równy tej wartości. Kąt 45° ma tangens równy 1, co oznacza, że długości obu boków są równe. Dla kąta 60°, tangens wynosi √3, co wskazuje na dominację długości przeciwległej nad przyległą. Natomiast dla kąta 90°, tangens jest nieokreślony, ponieważ cosinus 90° wynosi 0, co prowadzi do dzielenia przez zero.
Wartości te są niezwykle ważne w praktycznych zastosowaniach, takich jak obliczenia w geometrii czy analizie funkcji. Znajomość tych wartości pozwala na szybkie i efektywne rozwiązywanie problemów związanych z kątami w różnych kontekstach matematycznych.
Graficzna interpretacja tangensa: jak wygląda wykres funkcji?
Wykres funkcji tangens jest niezwykle interesujący i pełen charakterystycznych cech. Funkcja ta jest okresowa, co oznacza, że powtarza swoje wartości w regularnych odstępach. Wykres tangensa ma postać falującą, z pionowymi asymptotami, które występują w punktach, gdzie cosinus kąta wynosi 0, czyli dla kątów 90°, 270°, 450° itd. Wartości tangensa rosną w nieskończoność, gdy zbliżają się do tych asymptot, a następnie spadają do ujemnych wartości po przejściu przez te punkty.Wykres tangensa wykazuje także symetrię względem początku układu współrzędnych, co oznacza, że tangens kąta -α jest równy -tan α. Dzięki temu, możemy zauważyć, że dla każdego kąta, którego tangens jest dodatni, istnieje kąt przeciwny, dla którego tangens jest ujemny. Ta cecha sprawia, że funkcja tangens jest użyteczna w różnych dziedzinach matematyki i nauki.
Jak odczytać wartości tangensa z wykresu?
Aby odczytać wartości tangensa z wykresu, należy zwrócić uwagę na osie współrzędnych. Oś pozioma reprezentuje kąt w radianach lub stopniach, natomiast oś pionowa przedstawia wartość tangensa. Wartości tangensa można łatwo zidentyfikować, obserwując, jak wykres przechodzi przez różne punkty. Na przykład, dla kąta 45°, wykres przecina oś y w punkcie 1, co oznacza, że tangens 45° wynosi 1.
W przypadku kątów bliskich 90°, wykres zbliża się do asymptoty pionowej, co wskazuje na to, że tangens staje się coraz większy. Warto zwrócić uwagę na to, że wartości tangensa dla kątów ujemnych są lustrzanym odbiciem wartości dla kątów dodatnich, co potwierdza symetrię funkcji. Zrozumienie, jak odczytywać wartości tangensa z wykresu, jest kluczowe dla analizy i zastosowania tej funkcji w różnych kontekstach matematycznych.
Zastosowanie tangensa w praktyce: gdzie go spotykamy na co dzień?
Tangens ma szerokie zastosowanie w wielu dziedzinach, w tym w matematyce, fizyce, inżynierii i architekturze. W matematyce, jest używany do rozwiązywania problemów związanych z kątami i długościami w trójkątach prostokątnych. W inżynierii, tangens pomaga w obliczeniach związanych z nachyleniem, co jest kluczowe w projektowaniu konstrukcji. W architekturze, funkcja tangens jest wykorzystywana do określenia kątów nachylenia dachów oraz w planowaniu przestrzeni.
W przypadku analizy danych, tangens jest stosowany w statystyce do obliczania współczynnika korelacji, co pozwala na lepsze zrozumienie relacji między zmiennymi. Ponadto, w grafice komputerowej, tangens jest wykorzystywany do obliczeń związanych z perspektywą, co ma kluczowe znaczenie w tworzeniu realistycznych obrazów. Zrozumienie zastosowań tangensa w codziennym życiu może pomóc w lepszym wykorzystaniu tej funkcji w różnych kontekstach.Jak tangens pomaga w rozwiązywaniu problemów geometrycznych?
Tangens jest niezwykle przydatny w rozwiązywaniu problemów geometrycznych, zwłaszcza w kontekście trójkątów prostokątnych. Na przykład, gdy znamy długości dwóch boków trójkąta prostokątnego, możemy łatwo obliczyć kąt, używając tangensa. W praktyce, jeśli mamy do czynienia z budową, tangens pozwala na określenie wysokości budynku na podstawie odległości i kąta widzenia. Tego typu obliczenia są kluczowe w architekturze i inżynierii budowlanej.Innym przykładem jest zastosowanie tangensa w nawigacji. W systemach GPS, tangens jest używany do obliczania kątów, co pozwala na dokładne określenie pozycji na mapie. W przypadku analizy ruchu, tangens pomaga w obliczeniach związanych z kątami nachylenia dróg, co jest istotne dla bezpieczeństwa pojazdów. Zrozumienie, jak tangens wpływa na rozwiązywanie problemów geometrycznych, jest kluczowe dla efektywnego wykorzystania tej funkcji w praktyce.
Jak wykorzystać tangens w analizie danych i statystyce?
Tangens ma również zastosowanie w analizie danych i statystyce, gdzie może być użyty do modelowania relacji między zmiennymi. Na przykład, w analizie regresji, tangens jest wykorzystywany do obliczania współczynnika nachylenia, co pomaga w zrozumieniu, jak zmiana jednej zmiennej wpływa na inną. Umożliwia to nie tylko przewidywanie wyników, ale także identyfikację trendów w danych, co jest kluczowe w wielu dziedzinach, od ekonomii po nauki przyrodnicze.
W kontekście przyszłych trendów, rozwój technologii uczenia maszynowego i sztucznej inteligencji może jeszcze bardziej zwiększyć znaczenie tangensa w analizie danych. Algorytmy oparte na tangensie mogą być stosowane do optymalizacji modeli predykcyjnych, co pozwala na lepsze dostosowanie się do danych w czasie rzeczywistym. W miarę jak technologia się rozwija, umiejętność wykorzystania tangensa w bardziej zaawansowanych aplikacjach analitycznych stanie się coraz bardziej cenna dla specjalistów w różnych branżach.

