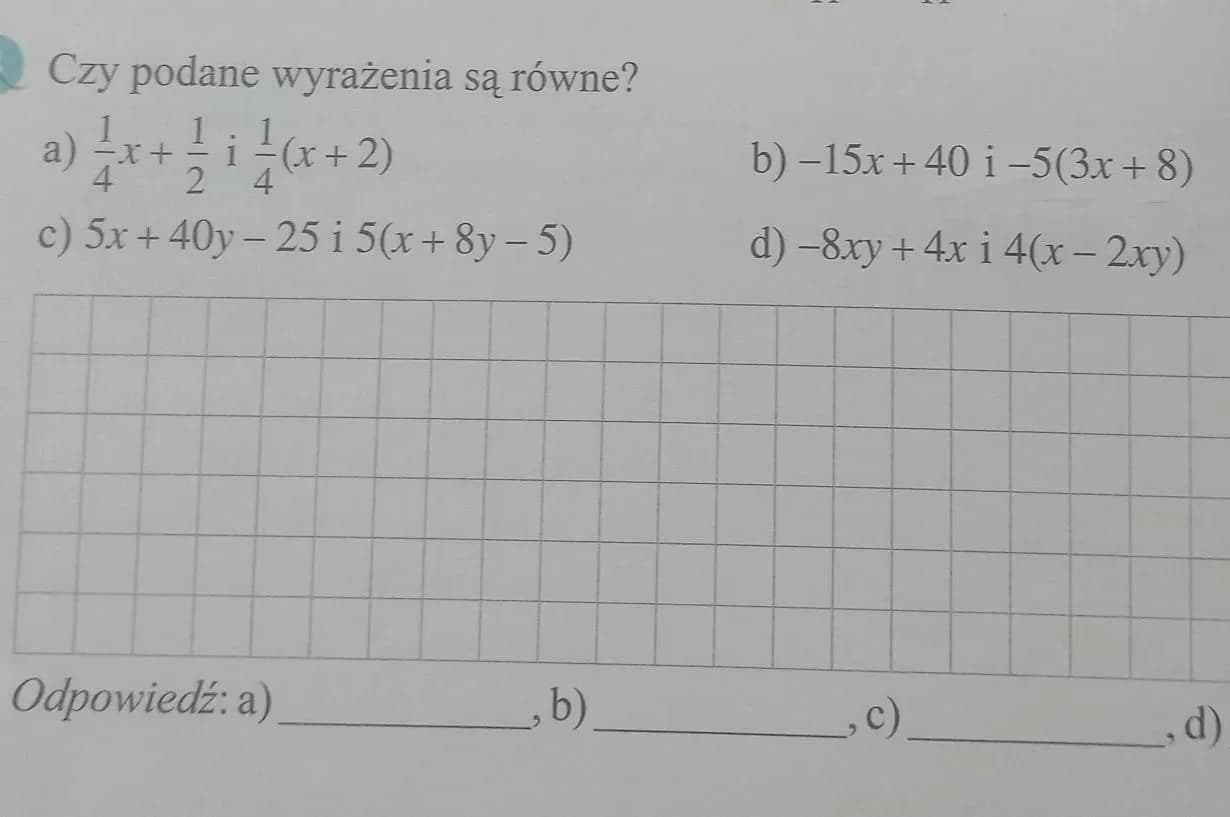Czy wyrażenia algebraiczne takie jak 3x, 3x + 4x i 10x - 6x są równe 3x? To pytanie zadaje sobie wiele osób, które uczą się algebry. W rzeczywistości, te trzy wyrażenia są równe 3x, co oznacza, że można je uprościć do tej samej formy. Zrozumienie równości w algebrze jest kluczowe, ponieważ pozwala na lepsze manipulowanie wyrażeniami i rozwiązywanie równań. Istnieją również wyrażenia, które nie są równe 3x, takie jak 3x + 1, co może być mylące dla uczniów.
W tym artykule przyjrzymy się, jak sprawdzić, czy wyrażenia algebraiczne są równe 3x. Omówimy zasady upraszczania wyrażeń oraz techniki identyfikacji równości. Dzięki temu zdobędziesz wiedzę, która pomoże Ci lepiej zrozumieć algebrę i jej zastosowania. Kluczowe wnioski:- Wyrażenia 3x, 3x + 4x oraz 10x - 6x są równe 3x po uproszczeniu.
- Wyrażenie 3x + 1 nie jest równe 3x, co pokazuje, że dodanie wartości do wyrażenia zmienia jego równoważność.
- Upraszczanie wyrażeń algebraicznych jest kluczowe dla zrozumienia równości i rozwiązywania równań.
- Znajomość technik porównywania wyrażeń pozwala na skuteczne weryfikowanie ich równości.
Jak sprawdzić, czy wyrażenia algebraiczne są równe 3x? Praktyczny przewodnik
Sprawdzanie, czy wyrażenia algebraiczne są równe 3x, jest kluczowym elementem algebry. Wymaga to zrozumienia, jak różne wyrażenia mogą być uproszczone lub przekształcone, aby ustalić ich równość. W tym przewodniku omówimy metody i procesy, które pomogą Ci weryfikować równość wyrażeń algebraicznych. Zrozumienie tego zagadnienia jest ważne dla skutecznego rozwiązywania równań i zadań matematycznych.
W algebrze, równość oznacza, że dwie strony równania mają tę samą wartość. Aby to sprawdzić, można używać różnych technik, takich jak upraszczanie wyrażeń, porównywanie ich wartości lub stosowanie właściwości algebraicznych. W kolejnych częściach artykułu przyjrzymy się szczegółowo tym metodom oraz ich praktycznemu zastosowaniu.
Zrozumienie pojęcia równości w algebrze i jego znaczenie
Równość w algebrze to fundamentalne pojęcie, które odnosi się do stwierdzenia, że dwie wartości są sobie równe. W kontekście wyrażeń algebraicznych oznacza to, że można je uprościć do tej samej postaci. Równość jest nie tylko istotna w rozwiązywaniu równań, ale także w analizie wyrażeń, co pozwala zrozumieć, jak różne elementy współpracują ze sobą w matematyce.
Ważne jest, aby zrozumieć, że równość nie zawsze jest oczywista. Czasami wyrażenia mogą wyglądać różnie, ale po uproszczeniu okazuje się, że są równe. Dlatego umiejętność sprawdzania równości jest niezbędna dla każdego ucznia algebry.
Kluczowe zasady upraszczania wyrażeń algebraicznych
Aby skutecznie sprawdzać równość wyrażeń algebraicznych, należy znać kilka kluczowych zasad upraszczania. Łączenie podobnych wyrazów to jedna z najważniejszych technik, która polega na dodawaniu lub odejmowaniu wyrazów o tych samych zmiennych. Na przykład, w wyrażeniu 3x + 4x można je uprościć do 7x.
Kolejną istotną techniką jest stosowanie własności rozdzielności (distributive property), która pozwala na rozdzielanie mnożenia nad dodawaniem. Na przykład, w wyrażeniu 2(3x + 4) można zastosować tę właściwość, aby uzyskać 6x + 8. Zrozumienie tych zasad jest kluczowe dla efektywnego upraszczania wyrażeń i weryfikowania ich równości.
Przykłady wyrażeń algebraicznych równych 3x oraz ich analiza
W tej części artykułu przyjrzymy się konkretnym przykładom wyrażeń algebraicznych, które upraszczają się do 3x. Zrozumienie, które wyrażenia są równe 3x, jest kluczowe dla skutecznego rozwiązywania równań i zadań matematycznych. Oto kilka przykładów, które pomogą w lepszym zrozumieniu tego zagadnienia. Pamiętaj, że niektóre wyrażenia, które na pierwszy rzut oka mogą wydawać się różne, po uproszczeniu mogą okazać się równe 3x.
Przykłady wyrażeń, które są równe 3x, obejmują 3x, 3x + 4x oraz 10x - 6x. Każde z tych wyrażeń można uprościć do 3x, co pokazuje, jak różne formy mogą prowadzić do tej samej wartości. W poniższej tabeli przedstawimy konkretne wyrażenia oraz kroki ich uproszczenia do 3x.
| Wyrażenie | Uproszczenie |
| 3x | 3x |
| 3x + 4x | 3x + 4x = 7x |
| 10x - 6x | 10x - 6x = 4x |
Wyrażenia, które upraszczają się do 3x: krok po kroku
Przyjrzyjmy się teraz wyrażeniom, które można uprościć do 3x. Na przykład, wyrażenie 3x + 4x można uprościć, łącząc podobne wyrazy. W tym przypadku dodajemy 3x i 4x, co daje nam 7x. Jednak, aby uzyskać 3x, możemy rozważyć inne wyrażenia, takie jak 10x - 6x. Po uproszczeniu, 10x - 6x daje 4x, a nie 3x, co pokazuje, że nie każde wyrażenie, które wygląda na złożone, jest równe 3x.
Inny przykład to 2(3x), które po zastosowaniu własności rozdzielności daje 6x. Warto zauważyć, że aby wyrażenie było równe 3x, musi być odpowiednio uproszczone. Wartości te mogą być mylące, dlatego kluczowe jest zrozumienie procesu upraszczania i umiejętność identyfikacji równości w wyrażeniach algebraicznych.
Analiza wyrażeń, które nie są równe 3x: dlaczego?
Nie każde wyrażenie algebraiczne jest równe 3x. Zrozumienie, dlaczego tak się dzieje, jest kluczowe dla nauki algebry. Na przykład, wyrażenie 3x + 1 nie jest równe 3x, ponieważ dodanie 1 zmienia wartość wyrażenia. Wartości algebraiczne, które wydają się podobne, mogą prowadzić do różnych wyników, co pokazuje, jak ważne jest dokładne upraszczanie i porównywanie wyrażeń.Inny przykład to 5x - 2x, które po uproszczeniu daje 3x, ale wyrażenie 4x nie jest równe 3x, ponieważ różnica między nimi wynosi x. Dlatego, aby zrozumieć, dlaczego niektóre wyrażenia nie są równe 3x, musimy dokładnie przyjrzeć się ich składnikom i procesowi uproszczenia. W poniższej tabeli przedstawimy kilka wyrażeń, które nie upraszczają się do 3x, oraz ich analizę.
| Wyrażenie | Uproszczenie |
| 3x + 1 | 3x + 1 (nie równe 3x) |
| 4x | 4x (nie równe 3x) |
| 5x - 2x | 3x (równe 3x) |
Czytaj więcej: Nauczyciel wspomagający: wymagania i kwalifikacje do pracy
Techniki identyfikacji równości w wyrażeniach algebraicznych
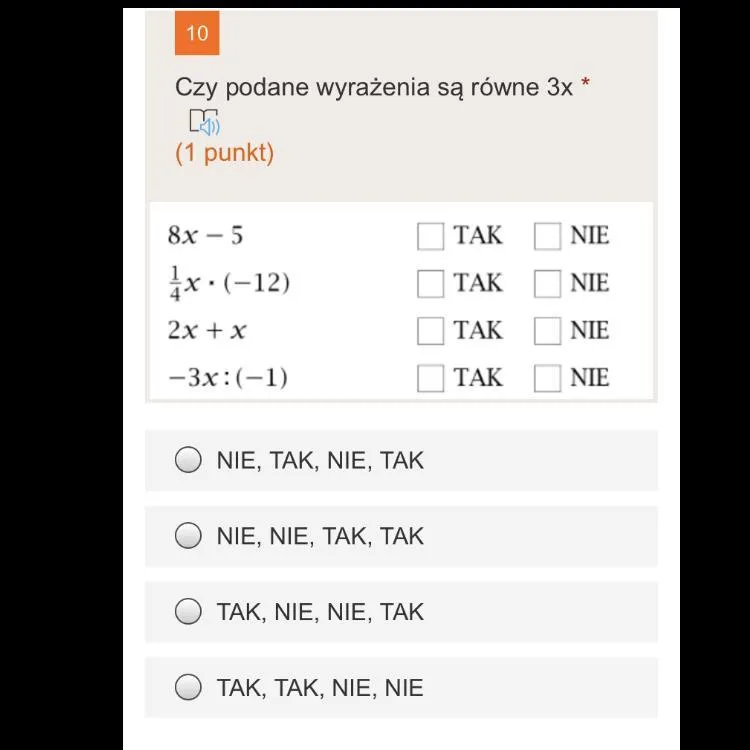
W tej części artykułu omówimy różne techniki, które można zastosować do identyfikacji równości w wyrażeniach algebraicznych, takich jak porównywanie metod oraz właściwości algebraiczne. Zrozumienie tych technik jest kluczowe, ponieważ pozwala na skuteczne weryfikowanie, czy dane wyrażenie jest równe 3x. Umiejętność ta jest niezbędna w algebrze, szczególnie podczas rozwiązywania równań i analizy wyrażeń.
Wśród metod identyfikacji równości można wymienić porównywanie wartości wyrażeń, co polega na podstawianiu konkretnych wartości zmiennych do wyrażeń i sprawdzaniu, czy uzyskujemy tę samą wartość. Kolejną techniką jest użycie właściwości algebraicznych, takich jak przemienność czy łączność, które pomagają w uproszczeniu wyrażeń i potwierdzeniu ich równości. W poniższych sekcjach przyjrzymy się tym technikom bliżej, aby lepiej zrozumieć, jak ich używać w praktyce.
Metody porównywania wyrażeń algebraicznych z 3x
Porównywanie wyrażeń algebraicznych z 3x można przeprowadzać na kilka sposobów. Jednym z najprostszych jest podstawienie, gdzie w miejsce zmiennej wstawiamy konkretne liczby, aby zobaczyć, czy wyrażenie jest równe 3x. Na przykład, jeśli mamy wyrażenie 5x - 2x, możemy podstawić wartości dla x, aby sprawdzić, czy wynik będzie równy 3x.
Inną metodą jest ewaluacja, która polega na obliczeniu wartości wyrażenia i porównaniu jej z 3x. Używając tej metody, możemy szybko zweryfikować, czy dane wyrażenie jest równe 3x. Ważne jest, aby pamiętać o zachowaniu porządku działań matematycznych podczas wykonywania obliczeń.
Jak używać właściwości algebraicznych do weryfikacji równości
Właściwości algebraiczne, takie jak przemienność i łączność, są niezwykle pomocne w weryfikacji równości wyrażeń. Przemienność pozwala na zmianę kolejności składników, co może uprościć wyrażenie. Na przykład, w wyrażeniu 2 + 3 możemy zamienić miejscami składniki i nadal uzyskać tę samą wartość.
Łączność natomiast umożliwia grupowanie składników w dowolny sposób, co również może ułatwić obliczenia. Na przykład, w wyrażeniu (2 + 3) + 4 możemy najpierw dodać 2 i 3, a następnie dodać 4, co da nam ten sam wynik, co dodawanie w innej kolejności. Zrozumienie i umiejętność stosowania tych właściwości jest kluczowe dla efektywnego sprawdzania równości w wyrażeniach algebraicznych.
Praktyczne ćwiczenia z wyrażeniami algebraicznymi i równością
Aby skutecznie zrozumieć, jak sprawdzać, czy wyrażenia algebraiczne są równe 3x, warto przeprowadzić kilka praktycznych ćwiczeń. Te ćwiczenia pomogą w identyfikacji wyrażeń, które upraszczają się do 3x oraz tych, które nie są równe tej wartości. Praktyka jest kluczowa, aby wzmocnić umiejętności w algebrze i lepiej zrozumieć procesy upraszczania oraz weryfikacji równości.
W ramach tych ćwiczeń, zachęcamy do rozwiązywania różnych przykładów oraz do samodzielnego sprawdzania, które wyrażenia są równe 3x. Możesz również spróbować znaleźć wyrażenia, które nie są równe 3x, co pomoże w rozwijaniu umiejętności analitycznych. Poniżej przedstawiamy kilka przykładów, które możesz rozwiązać samodzielnie.
Rozwiązywanie przykładów: jakie wyrażenia są równe 3x?
Oto kilka przykładów wyrażeń, które warto sprawdzić pod kątem równości z 3x: 6x - 3x, 9x - 6x, 3x + 0. Spróbuj uprościć każde z tych wyrażeń i określić, czy są one równe 3x. Pamiętaj, aby dokładnie przeanalizować każdy krok obliczeń, aby upewnić się, że rozumiesz proces upraszczania.Wyzwania: znajdowanie wyrażeń nie równych 3x w różnych kontekstach
Teraz czas na wyzwanie! Spróbuj znaleźć wyrażenia, które nie są równe 3x, takie jak 5x - 2x + 1 czy 4x. Zastanów się, dlaczego te wyrażenia nie są równe 3x i co sprawia, że mają inną wartość. Analiza tych przypadków pomoże Ci w lepszym zrozumieniu algebry i umiejętności weryfikacji równości.
Jak wykorzystać równości algebraiczne w codziennym życiu?
Znajomość równości algebraicznych, takich jak 3x, ma zastosowanie nie tylko w matematyce, ale także w codziennym życiu. Umiejętność analizy i upraszczania wyrażeń algebraicznych może pomóc w podejmowaniu lepszych decyzji finansowych, takich jak obliczanie wydatków czy oszczędności. Na przykład, jeśli planujesz budżet domowy, możesz użyć równości do porównania różnych wydatków i ustalenia, które z nich są bardziej opłacalne.
Dodatkowo, w erze cyfrowej, umiejętności algebraiczne stają się coraz bardziej istotne w kontekście analizy danych. Wiele branż, takich jak marketing czy inżynieria, wymaga umiejętności interpretacji danych i wyciągania wniosków na podstawie równości i proporcji. Zrozumienie równości algebraicznych umożliwia lepsze modelowanie sytuacji i przewidywanie wyników, co jest nieocenione w dynamicznie zmieniającym się świecie biznesu.