Wysokość w trójkącie to kluczowy element geometrii, który odgrywa ważną rolę w wielu obliczeniach. Definiowana jako prostopadłość od wierzchołka do przeciwległego boku, wysokość jest istotna dla zrozumienia kształtu i właściwości trójkątów. W każdym trójkącie można wyznaczyć trzy wysokości, które zawsze są prostopadłe do podstawy. Zrozumienie tego pojęcia jest niezbędne, aby skutecznie obliczać pole powierzchni trójkątów oraz rozwiązywać różnorodne zadania geometryczne.
W tym artykule przyjrzymy się, jak obliczyć wysokość w różnych rodzajach trójkątów, w tym prostokątnych, równobocznych i różnobocznych. Dzięki jasnym definicjom i praktycznym przykładom, każdy będzie mógł zrozumieć, jak wprowadzać to pojęcie w życie i wykorzystać je w praktyce. Kluczowe informacje:- Wysokość w trójkącie to prostopadłość od wierzchołka do przeciwległego boku.
- W każdym trójkącie można wyznaczyć trzy wysokości, które są zawsze prostopadłe do podstawy.
- Wysokość jest istotna dla obliczania pola powierzchni trójkątów.
- Metody obliczania wysokości różnią się w zależności od typu trójkąta.
- W trójkącie prostokątnym wysokość można łatwo obliczyć, korzystając z podstawowych wzorów geometrycznych.
- W trójkącie równobocznym wysokość można znaleźć, korzystając z odpowiednich wzorów, które uwzględniają długość boku.
- W trójkącie różnobocznym obliczanie wysokości wymaga nieco bardziej złożonych metod, ale jest wykonalne.
Wysokość w trójkącie - definicja i znaczenie w geometrii
Wysokość w trójkącie to kluczowy element geometrii, który definiuje się jako prostopadłość od wierzchołka do przeciwległego boku. Wysokość jest niezwykle istotna, ponieważ pozwala na lepsze zrozumienie kształtu trójkąta oraz jego właściwości. Każdy trójkąt ma trzy wysokości, które są zawsze prostopadłe do podstawy, co oznacza, że można je wyznaczyć w każdym rodzaju trójkąta. Zrozumienie tego pojęcia jest niezbędne do dalszych obliczeń i analizy geometrycznej.
Wysokość w trójkącie nie tylko pomaga w obliczaniu jego pola, ale także w zrozumieniu relacji między różnymi elementami trójkąta. Na przykład, wysokości mogą być używane do analizy symetrii i równowagi w trójkątach, co ma zastosowanie w wielu dziedzinach, takich jak architektura czy inżynieria. W związku z tym, znajomość definicji wysokości i jej znaczenia w geometrii jest fundamentalna dla każdego, kto chce zgłębiać tajniki matematyki i jej praktyczne zastosowania.Czym jest wysokość w trójkącie i jak ją zrozumieć?
Wysokość w trójkącie to odległość mierzona prostopadle od wierzchołka do linii prostej, która stanowi przeciwległy bok. Można ją zrozumieć jako miarę, która pokazuje, jak "wysoki" jest trójkąt w danym punkcie. Wysokość jest kluczowa dla analizy kształtów, ponieważ wpływa na obliczenia pól oraz innych właściwości trójkąta. Warto zauważyć, że wysokość może być różna dla każdego z wierzchołków, co czyni każdy trójkąt unikalnym pod względem geometrii.
Dlaczego wysokość jest istotna w obliczeniach geometrycznych?
Wysokość w trójkącie odgrywa kluczową rolę w obliczeniach geometrycznych, szczególnie przy obliczaniu pola powierzchni. Dzięki wysokości możemy łatwo określić, jak dużą przestrzeń zajmuje dany trójkąt. Wzór na pole trójkąta, który wykorzystuje wysokość, to 1/2 * podstawa * wysokość. Bez znajomości wysokości, nie moglibyśmy dokładnie obliczyć tej wartości, co czyni ją fundamentalnym elementem w geometrii.Oprócz obliczeń pola, wysokość jest także istotna w analizie relacji między różnymi elementami trójkąta. Pomaga zrozumieć, jak różne wierzchołki i boki wpływają na kształt i proporcje trójkąta. Wysokość jest również używana w bardziej zaawansowanych koncepcjach, takich jak twierdzenie Pitagorasa czy w analizie symetrii trójkątów. Dlatego też, znajomość wysokości i jej zastosowań jest niezbędna dla każdego, kto pragnie zgłębiać geometrię i jej praktyczne zastosowania.
Jak obliczyć wysokość w różnych typach trójkątów?
Obliczanie wysokości w trójkątach różni się w zależności od ich rodzaju. W każdym przypadku, znajomość podstawowych właściwości trójkątów oraz odpowiednich wzorów jest kluczowa. W tej sekcji przyjrzymy się, jak obliczyć wysokość w trójkątach prostokątnych, równobocznych oraz różnobocznych, aby lepiej zrozumieć różnorodność metod i podejść do tego zagadnienia.Metody obliczania wysokości w trójkącie prostokątnym
W trójkącie prostokątnym obliczanie wysokości jest stosunkowo proste, ponieważ jedna z wysokości jest jednocześnie jedną z krawędzi. Wysokość w tym przypadku jest mierzona od kąta prostego do przeciwległego boku. Można ją obliczyć, korzystając z podstawowego wzoru na pole trójkąta, który brzmi: pole = 1/2 * podstawa * wysokość. Znając pole i długość podstawy, możemy łatwo obliczyć wysokość, przekształcając wzór.
Wysokość można również określić, korzystając z twierdzenia Pitagorasa, które odnosi się do długości boków trójkąta prostokątnego. Dla trójkąta o bokach a, b i c (gdzie c to przeciwległy bok), wysokość h można obliczyć jako: h = (a * b) / c. Dzięki tym metodom, obliczanie wysokości w trójkącie prostokątnym staje się łatwe i intuicyjne.
| Typ trójkąta | Wzór na wysokość |
|---|---|
| Trójkąt prostokątny | h = (a * b) / c |
Wysokość w trójkącie równobocznym - jak ją znaleźć?
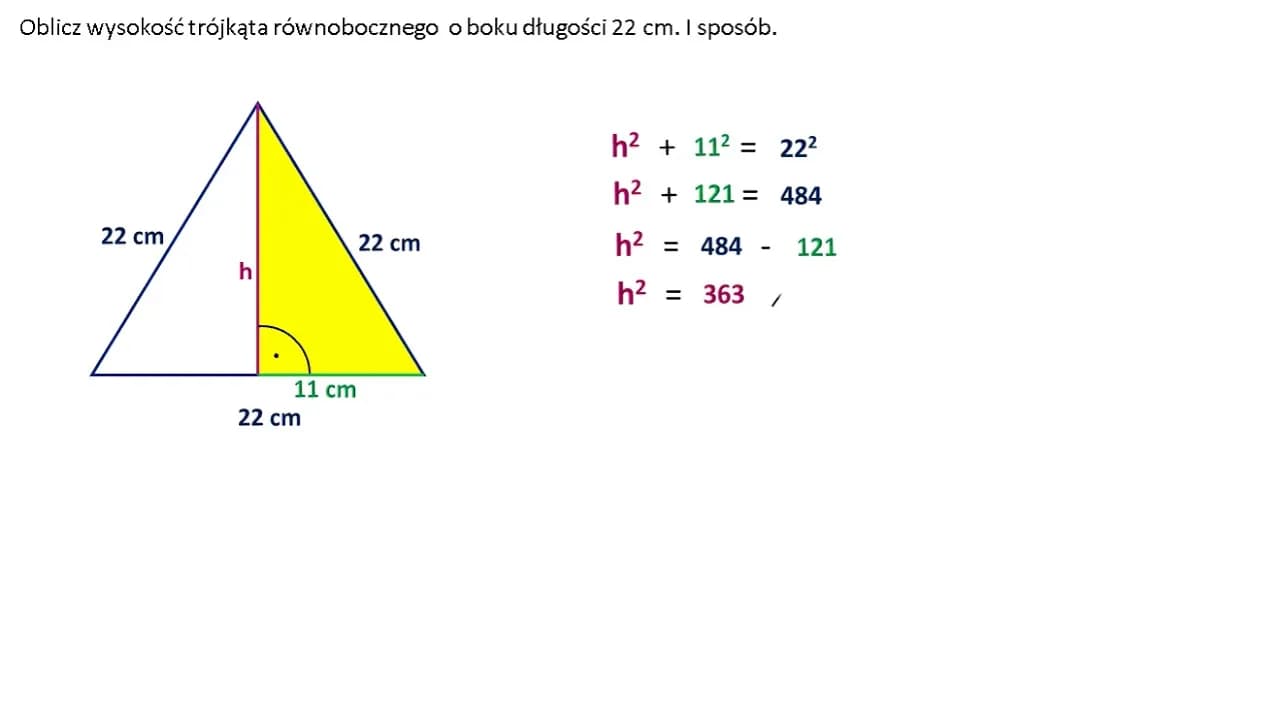
W trójkącie równobocznym, gdzie wszystkie boki są równe, wysokość można obliczyć, korzystając z prostego wzoru. Dla boku o długości a, wysokość h oblicza się za pomocą wzoru: h = (√3 / 2) * a. Dzięki temu wzorowi, możemy szybko określić wysokość trójkąta równobocznego, co jest szczególnie przydatne w zadaniach geometrycznych.
Obliczając wysokość w trójkącie równobocznym, warto pamiętać, że wysokość dzieli trójkąt na dwa mniejsze trójkąty prostokątne, co również można wykorzystać w obliczeniach. Ta metoda jest nie tylko efektywna, ale także pozwala na lepsze zrozumienie struktury trójkąta równobocznego.
Obliczanie wysokości w trójkącie różnobocznym - krok po kroku
Obliczanie wysokości w trójkącie różnobocznym jest nieco bardziej skomplikowane niż w przypadku trójkątów prostokątnych czy równobocznych. Wysokość można znaleźć, wykorzystując wzór Herona do obliczenia pola trójkąta, a następnie przekształcając go, aby wyznaczyć wysokość. Najpierw należy obliczyć obwód trójkąta, a następnie pole, korzystając z wzoru: pole = √(s * (s - a) * (s - b) * (s - c)), gdzie s to półobwód, a a, b, c to długości boków trójkąta.
Po obliczeniu pola, wysokość h można znaleźć z wzoru: h = (2 * pole) / podstawa. W tym przypadku podstawą może być dowolny bok trójkąta, a wysokość zostanie obliczona w odniesieniu do tego boku. Dzięki temu podejściu, można skutecznie obliczyć wysokość w trójkącie różnobocznym, nawet gdy jego boki są różnych długości.
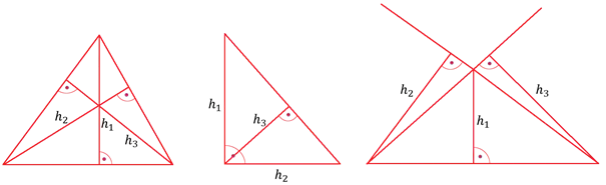
Wizualizacja wysokości w trójkącie - diagramy i przykłady
Wizualizacja wysokości w trójkącie jest kluczowa dla lepszego zrozumienia tego pojęcia. Diagramy ilustrujące wysokości pomagają zobaczyć, jak wysokości są rozmieszczone w trójkącie i jak wpływają na jego kształt. Wysokości w trójkącie różnobocznym mogą być różne, co sprawia, że ich wizualizacja jest szczególnie ważna. Ułatwia to również zrozumienie, jak wysokości wpływają na obliczenia pól i inne właściwości geometryczne.
Przykłady diagramów mogą obejmować trójkąty prostokątne, równoboczne i różnoboczne, gdzie każda wysokość jest pokazana jako linia prostopadła do odpowiedniego boku. Dzięki tym wizualizacjom, uczniowie i studenci mogą lepiej zrozumieć, jak obliczenia dotyczące wysokości są realizowane w praktyce, co pomaga w nauce geometrii.
Przykłady diagramów ilustrujących wysokość w trójkącie
Diagramy są niezwykle pomocne w zrozumieniu, jak wysokość jest reprezentowana w różnych typach trójkątów. Na przykład, w trójkącie prostokątnym, wysokość jest linią prostopadłą z kąta prostego do przeciwległego boku, co można zobaczyć na prostym diagramie. W trójkącie równobocznym, wysokość dzieli trójkąt na dwa mniejsze trójkąty prostokątne, co również można wizualizować na diagramie. Takie ilustracje pomagają zrozumieć, jak wysokości wpływają na kształt trójkąta oraz jak są używane w obliczeniach geometrycznych.
Zastosowanie wysokości w praktycznych zadaniach geometrycznych
Wysokość w trójkącie ma wiele praktycznych zastosowań w zadaniach geometrycznych. Na przykład, znajomość wysokości jest niezbędna do obliczenia pola trójkąta, co jest kluczowe w wielu dziedzinach, takich jak architektura czy inżynieria. Wysokość jest również używana w problemach związanych z symetrią i równowagą trójkątów. W praktyce, błędy w obliczeniach wysokości mogą prowadzić do nieprawidłowych wyników, dlatego ważne jest, aby dokładnie zrozumieć, jak obliczać i stosować wysokość w różnych kontekstach.
Jak wykorzystać wysokości trójkątów w projektowaniu i architekturze
Wysokości trójkątów mają kluczowe znaczenie nie tylko w matematyce, ale również w projektowaniu i architekturze. Zrozumienie, jak wysokości wpływają na stabilność i estetykę konstrukcji, pozwala architektom na tworzenie innowacyjnych rozwiązań. Na przykład, w projektach dachów, wysokość trójkątów może być wykorzystana do optymalizacji przepływu wody i efektywności energetycznej budynków. Zastosowanie trójkątnych struktur wsporczych może zwiększyć odporność na wiatry i inne obciążenia, co jest szczególnie ważne w regionach o zmiennych warunkach atmosferycznych.
Dodatkowo, zastosowanie trójkątów w sztuce i designie wnętrz, gdzie wysokości są kluczowe dla proporcji i harmonii, może wpłynąć na postrzeganie przestrzeni przez użytkowników. Przykładowo, odpowiednio zaprojektowane trójkątne elementy dekoracyjne mogą wprowadzić do pomieszczenia wrażenie głębi i dynamiki. W ten sposób, znajomość wysokości trójkątów staje się nie tylko narzędziem matematycznym, ale także praktycznym rozwiązaniem w tworzeniu funkcjonalnych i estetycznych przestrzeni.