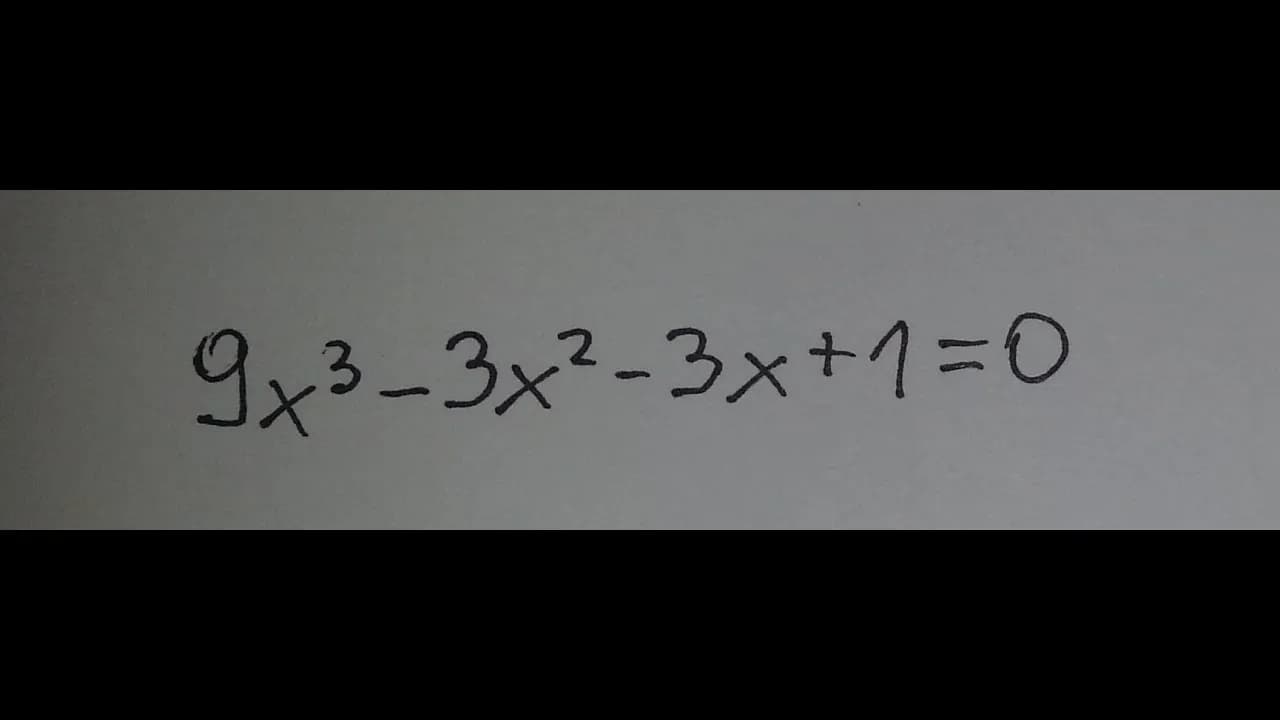Równania sześcienne, znane także jako równania stopnia trzeciego, są istotnym zagadnieniem w matematyce. Ich rozwiązanie może być wyzwaniem, jednak istnieje wiele metod, które pozwalają na skuteczne znalezienie pierwiastków. W tym artykule przyjrzymy się najpopularniejszym technikom, w tym metodzie Cardano, która umożliwia przekształcenie równania do formy \(x^3 + px + q = 0\) oraz znalezienie jego pierwiastków przy użyciu specjalnych wzorów.
Oprócz metody Cardano, omówimy również inne podejścia, takie jak syntetyczne dzielenie oraz metody numeryczne, które mogą być przydatne w różnych sytuacjach. Dzięki tym informacjom, czytelnicy będą mogli lepiej zrozumieć, jak rozwiązywać równania trzeciego stopnia i zastosować te techniki w praktyce. Kluczowe informacje:- Równanie sześcienne ma postać \(ax^3 + bx^2 + cx + d = 0\) i może mieć od jednego do trzech pierwiastków.
- Metoda Cardano pozwala na przekształcenie równania do formy, która ułatwia znalezienie pierwiastków.
- Syntetyczne dzielenie jest efektywną metodą obliczeniową, która może uprościć proces rozwiązywania równań.
- Metody numeryczne, takie jak metoda Newtona, są alternatywnym podejściem do rozwiązywania równań sześciennych, szczególnie w przypadkach, gdy inne metody są trudne do zastosowania.
- Praktyczne przykłady rozwiązań równań sześciennych pomogą zrozumieć zastosowanie omawianych metod w rzeczywistych sytuacjach.
Jak rozwiązać równanie 3 stopnia – podstawowe metody i definicje
Równanie stopnia trzeciego, znane również jako równanie sześcienne, ma kluczowe znaczenie w matematyce. Jego ogólna postać to \(ax^3 + bx^2 + cx + d = 0\), gdzie \(a\), \(b\), \(c\) i \(d\) są współczynnikami, a \(x\) jest zmienną. W odróżnieniu od równań niższego stopnia, równania sześcienne mogą mieć od jednego do trzech pierwiastków, co czyni je bardziej złożonymi. Zrozumienie ich struktury i właściwości jest istotne dla rozwiązywania problemów matematycznych oraz zastosowań w różnych dziedzinach nauki.
Równania sześcienne pojawiają się nie tylko w teorii matematycznej, ale także w praktycznych zastosowaniach, takich jak inżynieria czy ekonomia. Ich rozwiązanie pozwala na modelowanie zjawisk i procesów, co czyni je niezwykle użytecznymi. W tej sekcji przyjrzymy się bliżej definicji równań sześciennych oraz ich znaczeniu w kontekście rozwiązywania problemów.
Co to jest równanie 3 stopnia i jego charakterystyka?
Równanie 3 stopnia, czyli równanie sześcienne, ma postać ogólną \(ax^3 + bx^2 + cx + d = 0\). Współczynnik \(a\) musi być różny od zera, aby równanie miało charakter sześcienny. Kluczowe cechy równań sześciennych obejmują możliwość posiadania trzech pierwiastków, które mogą być rzeczywiste lub zespolone. Równania te mogą mieć także różne formy, w tym jedną lub więcej wielokrotnych pierwiastków, co wpływa na ich graficzną reprezentację oraz zachowanie funkcji.
Ważnym aspektem równań sześciennych jest ich związek z pojęciem krzywych sześciennych, które są wykresami funkcji sześciennych. Analiza tych równań oraz ich charakterystyka pozwala na lepsze zrozumienie zjawisk matematycznych i ich zastosowań w praktyce. W następnej sekcji omówimy kluczowe pojęcia związane z równaniami sześciennymi, które są niezbędne do ich zrozumienia i rozwiązywania.Jakie są podstawowe pojęcia związane z równaniami sześciennymi?
Równania sześcienne, czyli równania stopnia trzeciego, zawierają kilka kluczowych pojęć, które są niezbędne do ich zrozumienia. Pierwiastki równania to wartości zmiennej \(x\), które spełniają równanie, czyli sprawiają, że lewa strona równania jest równa zero. W przypadku równań sześciennych możemy mieć od jednego do trzech pierwiastków, które mogą być rzeczywiste lub zespolone.Ważnym elementem są również współczynniki, które są liczbami stojącymi przed poszczególnymi potęgami zmiennej \(x\). W ogólnej postaci równania sześciennego \(ax^3 + bx^2 + cx + d = 0\), \(a\), \(b\), \(c\) i \(d\) to współczynniki, gdzie \(a\) nie może być równe zeru. Kolejnym istotnym pojęciem jest stopień równania, który w przypadku równań sześciennych wynosi trzy. Stopień ten określa najwyższą potęgę zmiennej w równaniu, co wpływa na jego charakterystykę i liczbę pierwiastków.
Jak sprowadzić równanie do formy Cardano?
Aby sprowadzić równanie sześcienne do formy Cardano, należy wykonać kilka kroków. Najpierw, ogólne równanie \(ax^3 + bx^2 + cx + d = 0\) trzeba przekształcić, aby pozbyć się składnika kwadratowego. W tym celu dzielimy całe równanie przez \(a\) (jeśli \(a \neq 0\)), co daje nam postać \(x^3 + \frac{b}{a}x^2 + \frac{c}{a}x + \frac{d}{a} = 0\).
Następnie, aby uprościć równanie, stosujemy zmianę zmiennej \(x = y - \frac{b}{3a}\). Dzięki temu przekształcamy równanie do formy \(y^3 + py + q = 0\), gdzie \(p\) i \(q\) są nowymi współczynnikami wyznaczonymi na podstawie przekształconego równania. Po wykonaniu tych kroków, równanie będzie gotowe do zastosowania metody Cardano do wyznaczania pierwiastków.
Jak znaleźć pierwiastki równania sześciennego za pomocą Cardano?
Aby znaleźć pierwiastki równania sześciennego przy użyciu metody Cardano, należy najpierw sprowadzić równanie do formy \(y^3 + py + q = 0\). Następnie, obliczamy wartości \(D = \left(\frac{q}{2}\right)^2 + \left(\frac{p}{3}\right)^3\). W zależności od wartości delty \(D\), możemy mieć różne liczby pierwiastków: jeśli \(D > 0\), istnieje jeden pierwiastek rzeczywisty i dwa zespolone; jeśli \(D = 0\), wszystkie pierwiastki są rzeczywiste i przynajmniej dwa z nich są równe; a jeśli \(D < 0\), wszystkie pierwiastki są rzeczywiste i różne.
Po obliczeniu delty, można znaleźć pierwiastki za pomocą wzorów Cardano. Używamy wzorów na pierwiastki, które zależą od wartości \(p\) i \(q\). Ostatecznie, po wyznaczeniu wartości \(y\), przekształcamy je z powrotem do postaci \(x\) za pomocą wcześniejszej zmiany zmiennej. To pozwala na uzyskanie pierwiastków równania sześciennego.
| Rodzaj delty (D) | Liczba pierwiastków |
| D > 0 | 1 rzeczywisty, 2 zespolone |
| D = 0 | 3 rzeczywiste (co najmniej 2 równe) |
| D < 0 | 3 różne rzeczywiste |
Syntetyczna dzielenie – efektywna metoda obliczeń
Syntetyczne dzielenie to jedna z metod, która znacznie upraszcza proces obliczeń związanych z równaniami sześciennymi. Jest to technika, która pozwala na szybkie dzielenie wielomianów przez liniowe czynniki, co jest szczególnie przydatne w przypadku równań trzeciego stopnia. Dzięki syntetycznemu dzieleniu można uzyskać pierwiastki równania bez potrzeby stosowania bardziej skomplikowanych metod, takich jak metoda Cardano. Proces ten jest nie tylko szybszy, ale także bardziej przejrzysty, co czyni go popularnym wyborem wśród uczniów i studentów matematyki.
W praktyce, syntetyczne dzielenie polega na wykonaniu serii prostych operacji arytmetycznych, które pozwalają na uzyskanie reszty z dzielenia wielomianu przez liniowy czynnik. Dzięki temu można szybko zidentyfikować pierwiastki równania oraz uprościć dalsze obliczenia. Metoda ta jest szczególnie efektywna, gdy znamy jeden z pierwiastków równania, co pozwala na dalsze dzielenie i redukcję stopnia wielomianu.
Jak zastosować syntetyczne dzielenie do równań 3 stopnia?
Aby zastosować syntetyczne dzielenie do równań trzeciego stopnia, należy najpierw zidentyfikować pierwiastek, przez który chcemy podzielić wielomian. Na przykład, jeśli mamy równanie \(x^3 - 6x^2 + 11x - 6 = 0\) i znamy, że \(x = 1\) jest pierwiastkiem, możemy rozpocząć proces dzielenia. Wpisujemy współczynniki równania w odpowiednich miejscach i wykonujemy operacje arytmetyczne, aby uzyskać nowy wielomian stopnia drugiego. Po wykonaniu dzielenia, możemy łatwo znaleźć pozostałe pierwiastki, dzieląc uzyskany wielomian przez \(x - 1\) lub stosując kolejne syntetyczne dzielenie.
- Wybierz pierwiastek, przez który chcesz dzielić równanie.
- Wpisz współczynniki równania w odpowiednich miejscach.
- Wykonaj operacje arytmetyczne, aby uzyskać nowy wielomian.
Jakie są zalety i ograniczenia syntetycznego dzielenia?
Syntetyczne dzielenie ma wiele zalety, które czynią je popularnym narzędziem w rozwiązywaniu równań sześciennych. Po pierwsze, jest to metoda znacznie szybsza i prostsza niż tradycyjne dzielenie wielomianów, co pozwala na oszczędność czasu i redukcję błędów obliczeniowych. Po drugie, syntetyczne dzielenie ułatwia identyfikację pierwiastków równania, co jest kluczowe w procesie rozwiązywania. Dodatkowo, metoda ta jest łatwa do nauczenia i zrozumienia, co czyni ją idealną dla uczniów i studentów.
Jednak syntetyczne dzielenie ma także swoje ograniczenia. Przede wszystkim, jest skuteczne tylko w przypadku, gdy znamy jeden z pierwiastków równania, co może nie zawsze być możliwe. Ponadto, metoda ta nie jest odpowiednia dla wielomianów o stopniu wyższym niż 3, co ogranicza jej zastosowanie w bardziej złożonych problemach. Warto również zauważyć, że syntetyczne dzielenie nie dostarcza pełnych informacji o wszystkich pierwiastkach, co może być istotne w niektórych kontekstach matematycznych.
Czytaj więcej: Co za emocje gra edukacyjna - rozwijaj emocjonalną inteligencję dziecka
Jak wykorzystać równania sześcienne w modelowaniu rzeczywistości
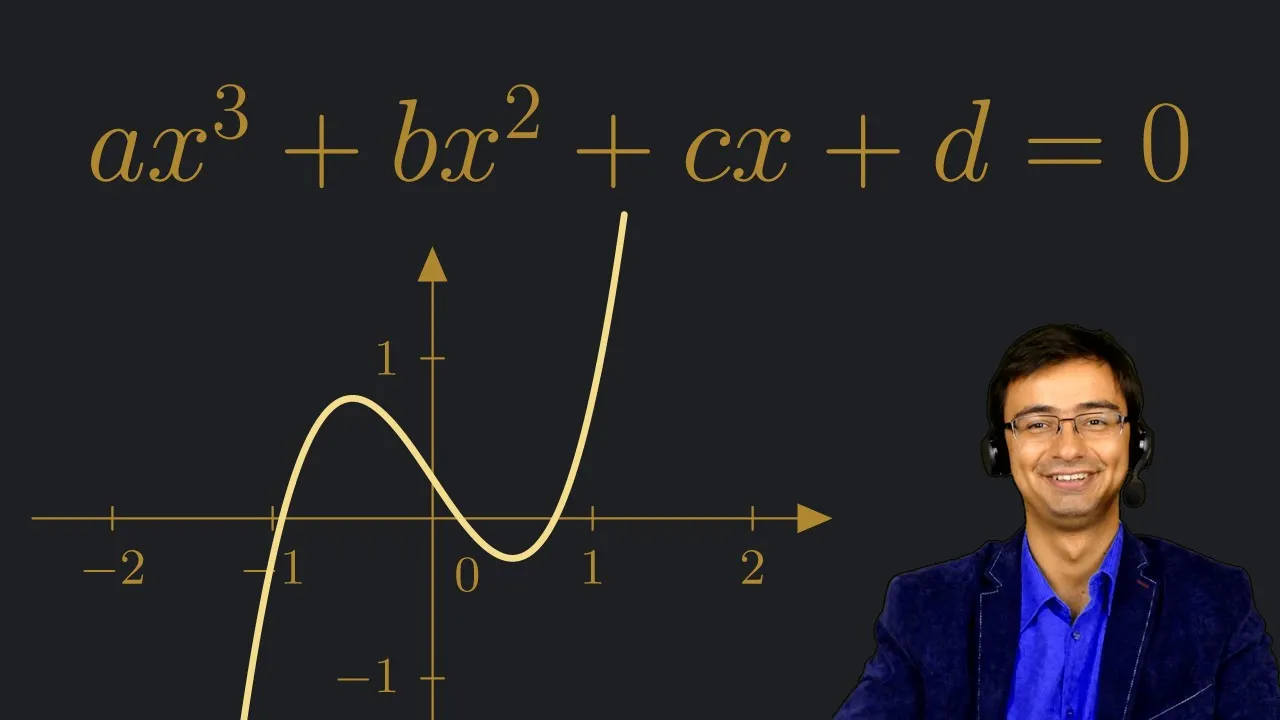
Równania sześcienne znajdują zastosowanie nie tylko w matematyce teoretycznej, ale także w praktycznych aspektach codziennego życia i różnych dziedzinach nauki. Na przykład, w inżynierii równania te mogą być używane do modelowania zjawisk fizycznych, takich jak ruchy ciał w przestrzeni czy analiza strukturalna budowli. Dzięki umiejętności rozwiązywania równań sześciennych inżynierowie mogą przewidywać, jak materiały zachowają się pod różnymi obciążeniami, co jest kluczowe w projektowaniu bezpiecznych i efektywnych konstrukcji.
Dodatkowo, w ekonomii równania sześcienne mogą służyć do modelowania złożonych zjawisk, takich jak zmiany cen na rynku lub analiza kosztów produkcji. Dzięki tym równaniom analitycy mogą przewidywać trendy i podejmować lepsze decyzje biznesowe. W przyszłości, wraz z rozwojem technologii, takich jak uczenie maszynowe i sztuczna inteligencja, umiejętność rozwiązywania równań sześciennych stanie się jeszcze bardziej cenna, ponieważ te techniki mogą być wykorzystywane do analizy dużych zbiorów danych i modelowania skomplikowanych procesów. Warto zatem rozwijać umiejętności związane z równaniami sześciennymi, aby lepiej przygotować się na wyzwania przyszłości.