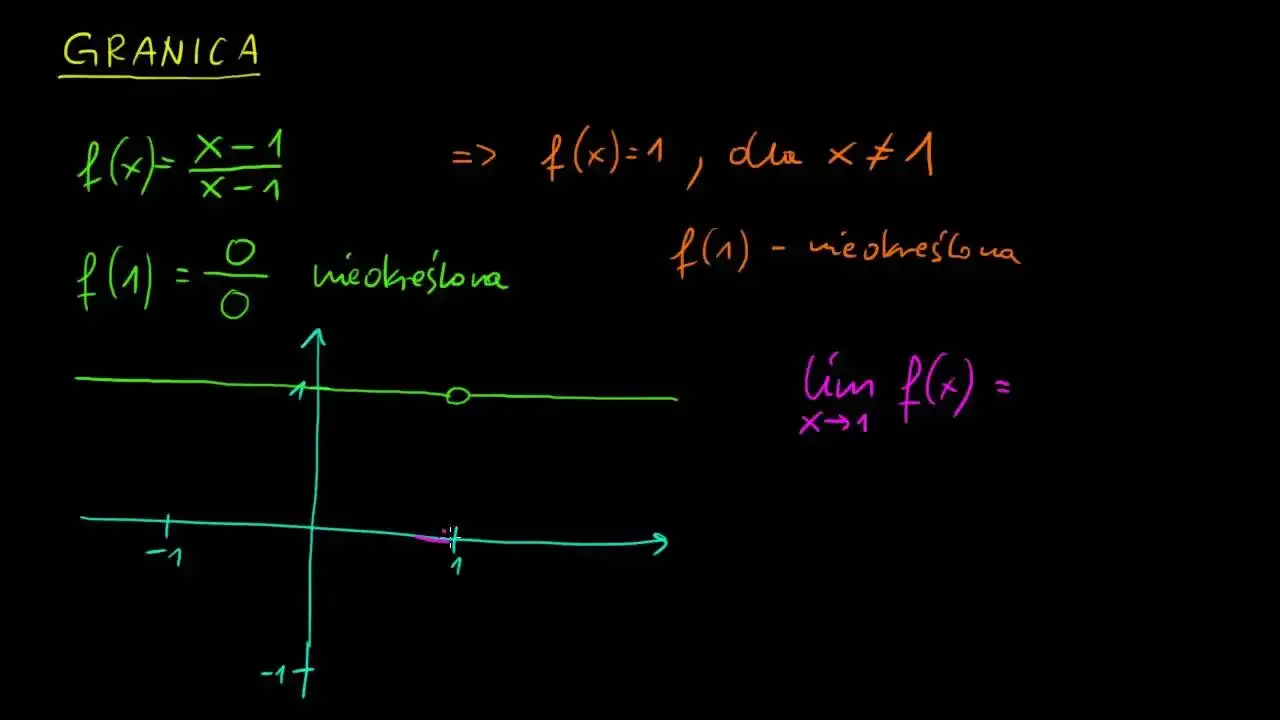
Granica w matematyce to kluczowy koncept, który odgrywa istotną rolę w analizie funkcji. W prostych słowach, granica to wartość, do której zbliżają się wyniki danej funkcji, gdy argumenty tej funkcji są coraz bliżej określonego punktu. Zrozumienie granic jest niezbędne, aby móc skutecznie analizować zmiany w zachowaniu funkcji, szczególnie w kontekście rachunku różniczkowego i rachunku całkowego.
W artykule przyjrzymy się nie tylko definicji granic, ale także ich właściwościom oraz zastosowaniom w praktyce. Oferujemy również konkretne przykłady obliczeń, które pomogą w lepszym zrozumieniu tego tematu. Dzięki temu czytelnicy będą mogli lepiej zrozumieć, jak granice wpływają na różne aspekty matematyki i dlaczego są tak istotne w dalszej nauce.
Kluczowe informacje:- Granica to wartość, do której zbliżają się wyniki funkcji, gdy argumenty są bliskie określonemu punktowi.
- Definicja granicy obejmuje koncepcję epsilon-delta, która jest fundamentalna w analizie matematycznej.
- Właściwości granic obejmują m.in. granice sumy, iloczynu i ilorazu funkcji.
- Obliczanie granic można przeprowadzać różnymi metodami, w tym przez podstawienie i faktoryzację.
- Granice są istotne w kontekście pojęcia ciągłości funkcji, co ma kluczowe znaczenie w analizie matematycznej.
Granica w matematyce: Definicja i podstawowe pojęcia
Granica w matematyce to fundamentalny koncept, który odgrywa kluczową rolę w analizie funkcji. W najprostszych słowach, granica to wartość, do której zbliżają się wyniki funkcji, gdy argumenty tej funkcji stają się coraz bliższe określonemu punktowi. To pojęcie jest niezbędne, aby zrozumieć, jak funkcje zachowują się w różnych sytuacjach, szczególnie gdy zbliżają się do punktów krytycznych.
Granice są również istotne w kontekście rachunku różniczkowego i rachunku całkowego, gdzie pomagają w definiowaniu pojęć takich jak pochodna i całka. Dzięki granicom możemy analizować zmiany w funkcjach oraz ich zachowanie w okolicach punktów, które mogą być problematyczne, takich jak punkty nieciągłości czy ekstremalne wartości. Zrozumienie granic jest więc kluczowe dla dalszej nauki matematyki i jej zastosowań w różnych dziedzinach.
Kluczowe właściwości granic w matematyce: Zrozumienie ich znaczenia
Granice mają kilka kluczowych właściwości, które są niezwykle istotne w matematyce. Jedną z podstawowych właściwości jest to, że granica sumy funkcji jest równa sumie granic tych funkcji. Oznacza to, że jeśli mamy dwie funkcje f(x) i g(x), to lim (f(x) + g(x)) = lim f(x) + lim g(x). Podobnie, granica iloczynu funkcji jest równa iloczynowi ich granic. Te zasady pozwalają na uproszczenie obliczeń i ułatwiają analizę zachowań funkcji w pobliżu określonych punktów.
Inną istotną właściwością jest granica ilorazu funkcji, która jest równa ilorazowi ich granic, pod warunkiem że granica funkcji w mianowniku nie jest równa zeru. To oznacza, że lim (f(x) / g(x)) = lim f(x) / lim g(x), jeśli lim g(x) ≠ 0. Te właściwości granic są nie tylko teoretyczne, ale mają praktyczne zastosowanie przy rozwiązywaniu równań i analizowaniu funkcji w kontekście rachunku różniczkowego i rachunku całkowego.
Jakie są podstawowe zasady dotyczące granic funkcji?
Podstawowe zasady dotyczące granic funkcji są kluczowe dla ich obliczania. Najważniejszą zasadą jest zasada podstawienia, która polega na tym, że jeśli funkcja jest ciągła w punkcie, to granica tej funkcji w tym punkcie jest równa wartości funkcji. To oznacza, że lim f(x) = f(a), jeżeli f(x) jest ciągła w punkcie a. Dzięki tej zasadzie można łatwo obliczać granice dla funkcji, które nie mają punktów nieciągłości.
Inną ważną zasadą jest zasada faktoryzacji, która polega na przekształceniu funkcji w taki sposób, aby uprościć obliczenia granic. Często, gdy mamy funkcję, która prowadzi do formy nieoznaczonej, możemy spróbować wyznaczyć granicę przez faktoryzację. Na przykład, jeśli mamy wyrażenie, które prowadzi do 0/0, możemy spróbować wyznaczyć granicę, dzieląc przez wspólny czynnik. Te zasady są nieocenione w praktyce i pomagają w efektywnym obliczaniu granic.
Czytaj więcej: Ile lat po szkole możesz zdawać maturę - kompletny poradnik dla absolwenta
Przykłady obliczeń granic: Krok po kroku do zrozumienia
Obliczanie granic funkcji to kluczowy element analizy matematycznej. W tej sekcji skupimy się na dwóch typach funkcji: liniowych i kwadratowych. Zrozumienie, jak obliczać granice dla tych funkcji, jest podstawą do dalszej nauki w matematyce. Przykłady te pomogą w praktycznym zastosowaniu teorii granic, co jest niezbędne do ich właściwego zrozumienia.
Rozpoczniemy od funkcji liniowej, która ma prostą formę i łatwo ją analizować. Następnie przejdziemy do funkcji kwadratowej, która wprowadza dodatkowe złożoności. Obie te funkcje są powszechnie używane w różnych dziedzinach matematyki i inżynierii, dlatego ich zrozumienie jest kluczowe.
| Typ funkcji | Przykład | Granica |
|---|---|---|
| Funkcja liniowa | f(x) = 2x + 3 | lim (x → 1) f(x) = 5 |
| Funkcja kwadratowa | g(x) = x² - 4 | lim (x → 2) g(x) = 0 |
Jak obliczyć granice funkcji liniowych i kwadratowych?
Obliczanie granic dla funkcji liniowych jest stosunkowo proste. Na przykład, dla funkcji f(x) = 2x + 3, chcąc obliczyć granicę, możemy po prostu podstawić wartość x do funkcji. Dla granicy lim (x → 1) f(x), otrzymujemy f(1) = 2(1) + 3 = 5. To pokazuje, że granica funkcji liniowej w danym punkcie jest równa wartości funkcji w tym punkcie, ponieważ funkcja jest ciągła.
W przypadku funkcji kwadratowej, na przykład g(x) = x² - 4, sytuacja jest nieco bardziej złożona. Chcąc obliczyć granicę lim (x → 2) g(x), również podstawiamy wartość x. Otrzymujemy g(2) = 2² - 4 = 0. Możemy zauważyć, że w tym przypadku granica również odpowiada wartości funkcji w danym punkcie. Funkcje kwadratowe mogą jednak prowadzić do form nieoznaczonych, na przykład 0/0, co wymaga dodatkowych technik, takich jak faktoryzacja, aby dokładniej obliczyć granice w bardziej złożonych przypadkach.Przykłady obliczeń granic funkcji wymiernych i trygonometrycznych
Obliczanie granic dla funkcji wymiernych i trygonometrycznych jest istotnym elementem analizy matematycznej. Funkcje wymierne, które są ilorazami dwóch wielomianów, mogą prowadzić do różnych form nieoznaczonych, takich jak 0/0. W takich przypadkach, aby obliczyć granice, często stosuje się faktoryzację lub uproszczenie wyrażenia. Na przykład, dla funkcji f(x) = (x² - 1) / (x - 1), możemy zauważyć, że dla x = 1 otrzymujemy formę nieoznaczoną, więc faktoryzujemy do f(x) = (x + 1) i obliczamy granicę.
Funkcje trygonometryczne, takie jak sinus i cosinus, również mają swoje specyficzne reguły przy obliczaniu granic. Na przykład, dla funkcji g(x) = sin(x) / x, granica w punkcie 0 jest równa 1, co jest kluczowym wynikiem w analizie matematycznej. Obliczenia granic dla funkcji trygonometrycznych mogą być bardziej złożone, zwłaszcza gdy występują różne transformacje, ale znajomość podstawowych właściwości tych funkcji znacznie ułatwia proces.
Jak granice wpływają na pojęcie ciągłości funkcji?
Granice mają kluczowe znaczenie w zrozumieniu pojęcia ciągłości funkcji. Funkcja jest uznawana za ciągłą w punkcie, jeśli granica tej funkcji w tym punkcie jest równa wartości funkcji. To oznacza, że dla funkcji f(x) ciągłej w punkcie a, musi zachodzić lim (x → a) f(x) = f(a). W przypadku, gdy granica nie jest równa wartości funkcji, mówimy o punkcie nieciągłym.
W praktyce, zrozumienie granic i ich związku z ciągłością jest niezwykle istotne w analizie matematycznej. Na przykład, w kontekście wykresów funkcji, ciągłość oznacza, że możemy narysować wykres bez podnoszenia ołówka z papieru. Granice pomagają również w identyfikacji punktów, w których funkcja może zmieniać swoje zachowanie, co jest kluczowe przy rozwiązywaniu równań i modelowaniu matematycznym. Dlatego granice są fundamentem dla dalszego rozwoju wiedzy w matematyce, szczególnie w rachunku różniczkowym i całkowym.Praktyczne zastosowania granic w modelowaniu rzeczywistości
Granice w matematyce nie tylko stanowią fundament analizy funkcji, ale także mają szerokie zastosowanie w modelowaniu rzeczywistości w różnych dziedzinach. Na przykład, w inżynierii i nauce danych, granice są wykorzystywane do przewidywania zachowań systemów dynamicznych, takich jak przepływ cieczy czy zmiany temperatury. Dzięki zastosowaniu granic można modelować zjawiska, które zmieniają się w czasie, co jest kluczowe w rozwoju technologii i optymalizacji procesów.
Kolejnym interesującym zastosowaniem granic jest ich rola w uczeniu maszynowym. W kontekście algorytmów optymalizacji, takich jak gradient descent, granice pomagają zrozumieć, jak funkcje kosztu zmieniają się w pobliżu punktów krytycznych. To pozwala na efektywniejsze trenowanie modeli i poprawę ich dokładności. W miarę jak technologia się rozwija, zrozumienie granic i ich zastosowań stanie się jeszcze bardziej istotne, szczególnie w kontekście inteligencji sztucznej i analizy dużych zbiorów danych.