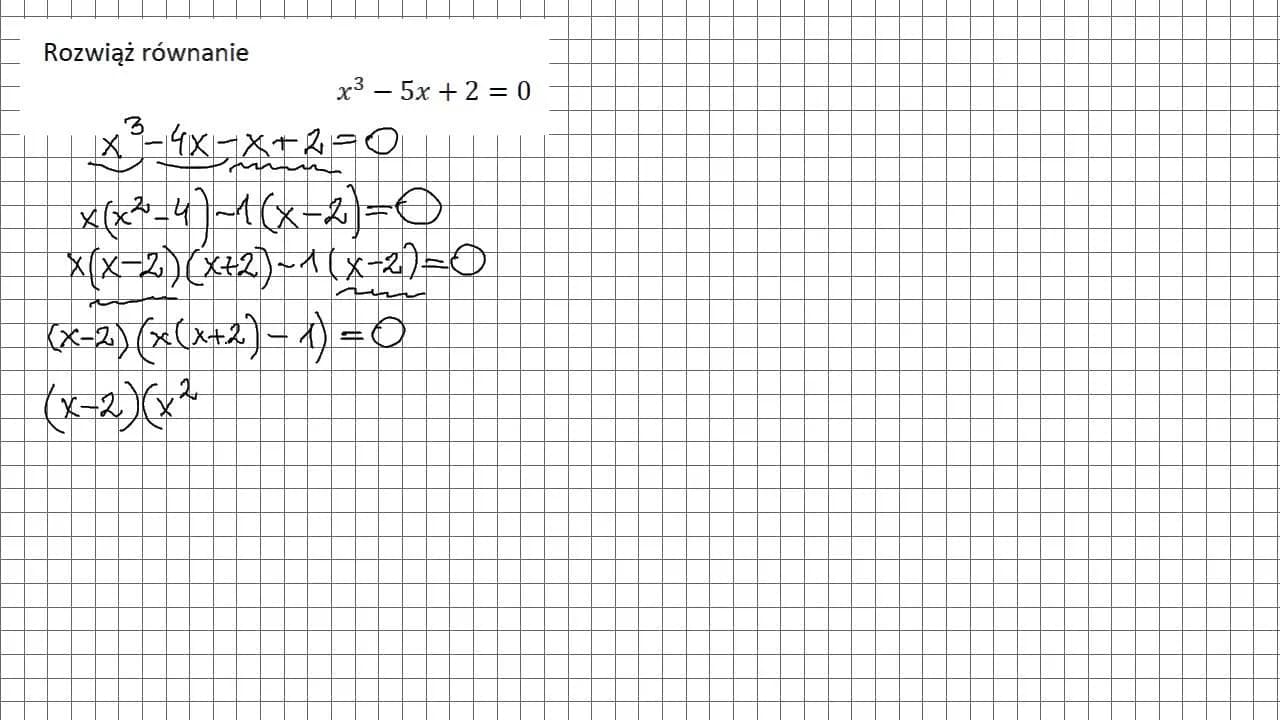Rozwiązywanie równań wielomianowych może wydawać się skomplikowane, ale w rzeczywistości istnieje wiele prostych metod, które można zastosować. Aby skutecznie rozwiązać równanie wielomianowe, należy sprowadzić je do postaci \(W(x) = 0\). W tej formie, pierwiastki wielomianu stają się jego rozwiązaniami. W artykule przedstawimy różne techniki, które pomogą w znalezieniu tych pierwiastków, zarówno dla prostych, jak i bardziej złożonych równań.
W pierwszej części omówimy podstawowe pojęcia związane z równaniami wielomianowymi, a następnie przejdziemy do konkretnych metod ich rozwiązywania. Dzięki tym informacjom, każdy będzie mógł lepiej zrozumieć, jak podejść do problemu i wyciągnąć właściwe wnioski.
Kluczowe wnioski:- Równania wielomianowe można sprowadzić do postaci \(W(x) = 0\), gdzie ich rozwiązaniami są pierwiastki.
- Wielomiany można klasyfikować według stopnia i współczynników, co ułatwia ich analizę.
- Faktoryzacja i wzór kwadratowy to podstawowe metody rozwiązywania równań.
- Zaawansowane techniki, takie jak podział syntetyczny i metoda Newtona, są przydatne w przypadku bardziej skomplikowanych równań.
- Wizualizacja rozwiązań na wykresach pomaga lepiej zrozumieć zachowanie funkcji i ich pierwiastki.
Jak rozwiązać równania wielomianowe - podstawowe metody
Równania wielomianowe to wyrażenia matematyczne, które mają postać W(x) = a_n x^n + a_{n-1} x^{n-1} + ... + a_1 x + a_0, gdzie a_n, a_{n-1}, ..., a_1, a_0 są współczynnikami, a n to stopień wielomianu. Aby rozwiązać równanie wielomianowe, należy sprowadzić je do postaci W(x) = 0, co pozwala znaleźć pierwiastki tego wielomianu. W praktyce oznacza to, że musimy znaleźć wartości x, które spełniają to równanie.
Przykładami równań wielomianowych mogą być: x^2 - 4 = 0, gdzie pierwiastkami są x = 2 oraz x = -2, oraz x^3 - 6x + 8 = 0, którego pierwiastki można znaleźć przy użyciu różnych metod. W obu przypadkach, celem jest znalezienie wartości x, które sprawiają, że równanie jest prawdziwe.
Zrozumienie równania wielomianowego - definicja i przykłady
Równanie wielomianowe to równanie, które można zapisać w formie wielomianu. Wielomiany są funkcjami, które mogą mieć różne stopnie, a ich rozwiązania to pierwiastki, które można znaleźć na różne sposoby. Na przykład, rozważmy równanie x^2 - 4 = 0. Możemy je rozwiązać, przekształcając je do postaci (x - 2)(x + 2) = 0, co daje nam pierwiastki x = 2 oraz x = -2.
Inny przykład to równanie x^3 - 6x + 8 = 0. Aby znaleźć pierwiastki tego równania, można skorzystać z różnych metod, takich jak faktoryzacja czy wzór kwadratowy. W tym przypadku, pierwiastki można znaleźć poprzez próbę podstawienia różnych wartości x lub użycie bardziej zaawansowanych technik, które zostaną omówione w dalszej części artykułu.
Klasyfikacja równań wielomianowych - stopień i współczynniki
Równania wielomianowe można klasyfikować na podstawie ich stopnia oraz współczynników. Stopień równania to najwyższa potęga zmiennej x w danym wielomianie. Na przykład, równanie 2x^3 + 3x^2 - x + 5 = 0 jest trzeciego stopnia, ponieważ najwyższa potęga x wynosi 3. Klasyfikacja ta ma kluczowe znaczenie, ponieważ różne metody rozwiązywania równań są stosowane w zależności od stopnia.
- Równania liniowe: Równania pierwszego stopnia, takie jak ax + b = 0.
- Równania kwadratowe: Równania drugiego stopnia, na przykład ax^2 + bx + c = 0.
- Równania sześcienne: Równania trzeciego stopnia, takie jak ax^3 + bx^2 + cx + d = 0.
Klasyfikacja równań wielomianowych pozwala na lepsze zrozumienie ich struktury i ułatwia wybór odpowiednich metod rozwiązywania. Wiedza o stopniu i współczynnikach jest kluczowa w dalszym procesie znajdowania pierwiastków.
Metody rozwiązywania równań wielomianowych - krok po kroku
Aby skutecznie rozwiązać równanie wielomianowe, istnieje wiele metod, które można zastosować. W tej części omówimy dwie podstawowe techniki: faktoryzację oraz wzór kwadratowy. Każda z tych metod ma swoje zastosowanie w zależności od stopnia wielomianu oraz jego współczynników. Dzięki tym technikom, można łatwo znaleźć pierwiastki równania, co jest kluczowe w dalszej analizie.
Faktoryzacja to jedna z najprostszych metod, która polega na rozkładaniu wielomianu na iloczyn prostszych wyrażeń. Z kolei wzór kwadratowy jest użyteczny w przypadku równań drugiego stopnia. W obu przypadkach, znajomość odpowiednich kroków pozwala na efektywne rozwiązywanie równań.
Faktoryzacja - prosty sposób na znalezienie pierwiastków
Faktoryzacja to metoda, która polega na przekształceniu wielomianu do postaci iloczynu. Umożliwia to łatwe wyznaczenie pierwiastków. Na przykład, rozważmy równanie x^2 - 5x + 6 = 0. Możemy je przekształcić do postaci (x - 2)(x - 3) = 0, co wskazuje, że pierwiastkami są x = 2 oraz x = 3. Proces faktoryzacji można przeprowadzić w kilku krokach:
- Znajdź dwa liczby, które mnożą się do c (wyrazu wolnego) i sumują się do b (współczynnika przy x).
- Rozłóż wielomian na iloczyn dwóch nawiasów.
- Ustaw każdy nawias równy zero i rozwiązuj dla x.
Faktoryzacja jest jedną z najczęściej stosowanych metod, ponieważ jest szybka i intuicyjna, zwłaszcza w przypadku równań kwadratowych. Warto jednak pamiętać, że nie wszystkie wielomiany dają się łatwo faktoryzować.
Wykorzystanie wzoru kwadratowego - kiedy i jak stosować
Wzór kwadratowy to kolejna skuteczna metoda rozwiązywania równań drugiego stopnia, która ma postać x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}. Używa się go, gdy równanie nie da się łatwo faktoryzować. Na przykład, dla równania 2x^2 + 3x - 2 = 0, możemy zastosować wzór kwadratowy, gdzie a = 2, b = 3, a c = -2.
Obliczenia wykonujemy według wzoru:
- Oblicz deltę: \Delta = b^2 - 4ac = 3^2 - 4 \cdot 2 \cdot (-2) = 9 + 16 = 25.
- Oblicz pierwiastki: x = \frac{-3 \pm \sqrt{25}}{2 \cdot 2} = \frac{-3 \pm 5}{4}.
Wynikiem będą pierwiastki x_1 = \frac{2}{4} = 0.5 oraz x_2 = \frac{-8}{4} = -2. Wzór kwadratowy jest uniwersalnym narzędziem, które można stosować w różnych sytuacjach, co czyni go niezwykle przydatnym w matematyce.
Wykorzystanie wzoru kwadratowego - kiedy i jak stosować
Wzór kwadratowy jest jedną z najważniejszych metod rozwiązywania równań wielomianowych drugiego stopnia. Jego ogólna postać to x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a}, gdzie a, b i c to współczynniki równania ax^2 + bx + c = 0. Metoda ta jest szczególnie przydatna, gdy równanie nie da się łatwo faktoryzować, a także w przypadkach, gdy chcemy uzyskać dokładne wartości pierwiastków.
Na przykład, rozważmy równanie 2x^2 + 3x - 2 = 0. Aby zastosować wzór kwadratowy, najpierw identyfikujemy współczynniki: a = 2, b = 3, c = -2. Następnie obliczamy deltę, która jest kluczowym elementem w tym procesie. Deltę obliczamy według wzoru: \Delta = b^2 - 4ac. W naszym przypadku, mamy \Delta = 3^2 - 4 \cdot 2 \cdot (-2) = 9 + 16 = 25.
- Jeśli \Delta > 0, równanie ma dwa różne pierwiastki.
- Jeśli \Delta = 0, równanie ma jeden podwójny pierwiastek.
- Jeśli \Delta < 0, równanie nie ma pierwiastków rzeczywistych.
W naszym przykładzie, ponieważ \Delta = 25, możemy obliczyć pierwiastki:
- x_1 = \frac{-3 + \sqrt{25}}{2 \cdot 2} = \frac{-3 + 5}{4} = \frac{2}{4} = 0.5
- x_2 = \frac{-3 - \sqrt{25}}{2 \cdot 2} = \frac{-3 - 5}{4} = \frac{-8}{4} = -2
Wynikiem są pierwiastki x_1 = 0.5 oraz x_2 = -2. Wzór kwadratowy jest uniwersalnym narzędziem, które można wykorzystać w różnych sytuacjach, co czyni go niezwykle przydatnym w matematyce.
Podział syntetyczny - efektywna metoda dla większych wielomianów
Podział syntetyczny to technika, która umożliwia efektywne rozwiązywanie równań wielomianowych, szczególnie dla wielomianów o stopniu większym niż 2. Metoda ta jest szybsza niż tradycyjne dzielenie wielomianów i pozwala na łatwe obliczenie wartości wielomianu dla danego pierwiastka. Aby zastosować podział syntetyczny, należy najpierw zidentyfikować pierwiastek, przez który będziemy dzielić, a następnie zorganizować współczynniki wielomianu w odpowiedni sposób.
Na przykład, rozważmy wielomian 2x^3 - 6x^2 + 2x - 4 i chcemy go podzielić przez x - 2. Współczynniki wielomianu to: 2, -6, 2, -4. Proces podziału syntetycznego wygląda następująco:
- Wpisz pierwiastek 2 po lewej stronie oraz współczynniki wielomianu w wierszu poniżej.
- Przeciągnij pierwszy współczynnik (2) w dół.
- Pomnóż ten współczynnik przez pierwiastek (2) i dodaj do kolejnego współczynnika (-6), co daje -2.
- Powtórz proces dla pozostałych współczynników, aż uzyskasz wynik.
W wyniku podziału uzyskujemy nowy wielomian 2x^2 - 2, a reszta wynosi 0, co oznacza, że x = 2 jest pierwiastkiem wielomianu. Podział syntetyczny jest więc skuteczną metodą, która może być stosowana do szybkiego znajdowania pierwiastków oraz uproszczenia większych wielomianów.
Metoda Newtona - przybliżone rozwiązania dla trudnych równań
Metoda Newtona to zaawansowana technika, która pozwala na znajdowanie przybliżonych rozwiązań równań wielomianowych. Jest to metoda iteracyjna, która wykorzystuje pochodne funkcji, aby zbliżyć się do rzeczywistego pierwiastka. Aby zastosować tę metodę, musimy znać początkowe przybliżenie pierwiastka oraz pochodną funkcji.
Na przykład, rozważmy równanie x^3 - 2x - 5 = 0. Załóżmy, że zaczynamy od przybliżenia x_0 = 2. Wtedy obliczamy wartość funkcji oraz jej pochodnej:
- Funkcja: f(x) = x^3 - 2x - 5.
- Pochodna: f'(x) = 3x^2 - 2.
Stosując wzór Newtona: x_{n+1} = x_n - \frac{f(x_n)}{f'(x_n)}, obliczamy kolejne przybliżenia:
- x_1 = 2 - \frac{f(2)}{f'(2)} = 2 - \frac{(2^3 - 2 \cdot 2 - 5)}{(3 \cdot 2^2 - 2)} = 2 - \frac{(8 - 4 - 5)}{10} = 2 - \frac{-1}{10} = 2.1
Kontynuując ten proces, możemy uzyskać coraz dokładniejsze przybliżenia pierwiastka. Metoda Newtona jest szczególnie użyteczna w przypadku trudnych równań, gdzie inne metody mogą zawodzić, a jej szybkość konwergencji czyni ją jedną z najpopularniejszych technik w analizie matematycznej.
Czytaj więcej: Hospitacja nauczyciela wspomagającego - jak przebiega i co musisz wiedzieć
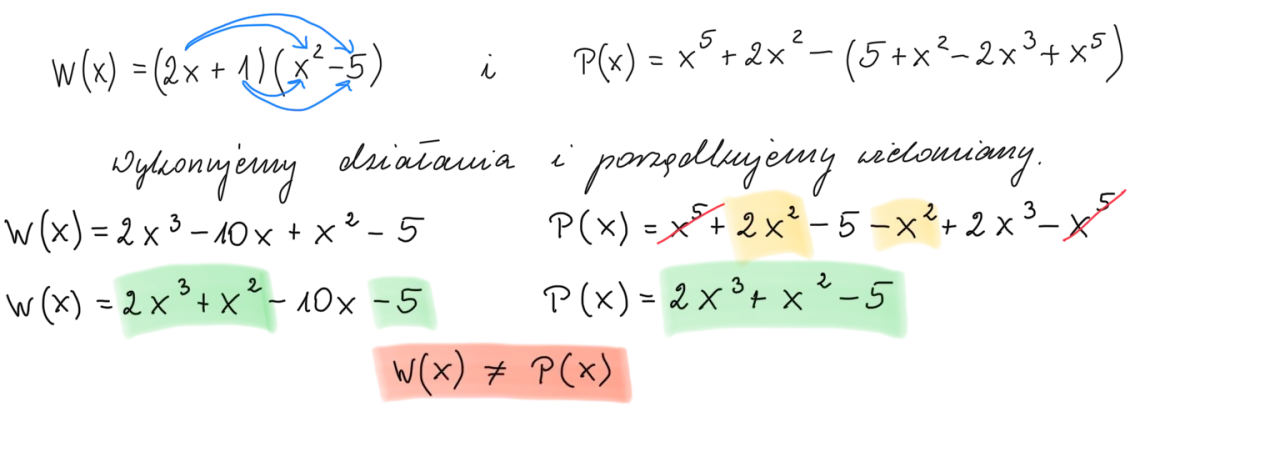
Wizualizacja rozwiązań równań wielomianowych - znaczenie wykresów
Wizualizacja równań wielomianowych poprzez wykresy jest kluczowym narzędziem w zrozumieniu ich zachowań i właściwości. Dzięki graficznemu przedstawieniu funkcji, możemy łatwo dostrzec miejsca zerowe, czyli pierwiastki równania, oraz inne istotne cechy, takie jak maksimum, minimum czy punkty przegięcia. Wykresy umożliwiają również analizę, jak zmieniają się wartości funkcji w zależności od zmiennych, co jest szczególnie pomocne w kontekście rozwiązywania równań.
Umiejętność interpretacji wykresów wielomianów pozwala na szybsze i dokładniejsze zrozumienie problemów matematycznych. Warto zauważyć, że różne stopnie wielomianów mają charakterystyczne kształty wykresów, co może pomóc w przewidywaniu ich zachowań. Na przykład, wykresy funkcji kwadratowej mają kształt parabol, podczas gdy funkcje sześcienne mogą mieć bardziej złożoną strukturę.
Graficzne przedstawienie pierwiastków - jak czytać wykresy
Umiejętność czytania wykresów równań wielomianowych jest niezbędna do identyfikacji pierwiastków i ich znaczenia. Pierwiastki wielomianu to miejsca, gdzie wykres przecina oś x, co oznacza, że dla tych wartości funkcja przyjmuje wartość zero. Na przykład, dla równania x^2 - 4 = 0, wykres parabolowy przecina oś x w punktach x = 2 oraz x = -2, co odpowiada pierwiastkom równania.
Aby skutecznie interpretować wykresy, warto zwrócić uwagę na kilka kluczowych elementów:
- Identifikacja miejsc zerowych, które wskazują pierwiastki równania.
- Obserwacja kierunku, w jakim wykres się porusza, co może wskazywać na zachowanie funkcji w nieskończoności.
- Analiza punktów przegięcia oraz ekstremów, które mogą być istotne w kontekście rozwiązywania równań.
| Równanie | Pierwiastki | Wykres |
|---|---|---|
| x^2 - 4 = 0 | x = 2, x = -2 |  |
| x^3 - 3x + 2 = 0 | x = 1, x = -1 |  |
Analiza zachowania funkcji - co mówi nam kształt wykresu
Analiza zachowania funkcji na podstawie jej wykresu jest kluczowa dla zrozumienia, jak zmieniają się wartości funkcji w różnych przedziałach. Kształt wykresu wielomianu dostarcza informacji o jego pierwiastkach, a także o tym, czy funkcja osiąga maksimum czy minimum. Na przykład, funkcje paraboliczne mają jedno minimum lub maksimum, podczas gdy funkcje sześcienne mogą mieć zarówno maksima, jak i minima.
Ważne cechy, które warto analizować, to:
- Punkty przegięcia, które wskazują na zmianę kierunku wykresu.
- Przebieg funkcji w nieskończoności, co może pomóc w przewidywaniu zachowań funkcji dla dużych wartości zmiennej.
- Wartości ekstremalne, które mogą być istotne w kontekście rozwiązywania problemów optymalizacyjnych.
Wykorzystanie technologii do analizy równań wielomianowych
W dzisiejszych czasach, technologia odgrywa kluczową rolę w analizie i rozwiązywaniu równań wielomianowych. Dzięki oprogramowaniu matematycznemu, takiemu jak MATLAB, Wolfram Alpha czy GeoGebra, możemy nie tylko szybko obliczać pierwiastki, ale również wizualizować zachowanie funkcji w sposób interaktywny. Takie narzędzia pozwalają na symulacje, które mogą pomóc w lepszym zrozumieniu dynamiki równań i ich zastosowań w różnych dziedzinach, takich jak inżynieria, ekonomia czy nauki przyrodnicze.
Co więcej, uczenie maszynowe zaczyna znajdować zastosowanie w prognozowaniu zachowań funkcji wielomianowych. Dzięki algorytmom, które potrafią analizować dane historyczne, możemy przewidywać, jak zmiany w parametrach równania wpłyną na jego pierwiastki oraz ogólne zachowanie wykresu. Ta nowa perspektywa otwiera drzwi do bardziej zaawansowanych analiz i modelowania, które mogą być niezwykle przydatne w badaniach naukowych oraz w zastosowaniach przemysłowych.
