Rozwiązywanie równań kwadratowych może wydawać się skomplikowane, ale z odpowiednimi metodami staje się prostsze. Równanie kwadratowe ma postać \(ax^2 + bx + c = 0\), gdzie \(a\) jest różne od zera. Kluczowym krokiem w rozwiązaniu takiego równania jest obliczenie delty, która jest wyrażona wzorem \(\Delta = b^2 - 4ac\). Delta pozwala na określenie liczby i rodzaju rozwiązań równania.
W niniejszym artykule przedstawimy różne metody rozwiązywania równań kwadratowych, w tym faktoryzację, uzupełnianie kwadratu oraz zastosowanie wzoru kwadratowego. Dzięki tym technikom każdy będzie mógł zrozumieć, jak skutecznie rozwiązać równanie kwadratowe i uniknąć najczęstszych błędów.
Kluczowe informacje:- Równanie kwadratowe ma postać \(ax^2 + bx + c = 0\), gdzie \(a \neq 0\).
- Delta, obliczana jako \(\Delta = b^2 - 4ac\), określa liczbę rozwiązań równania.
- Istnieją trzy główne metody rozwiązywania równań kwadratowych: faktoryzacja, uzupełnianie kwadratu i wzór kwadratowy.
- Faktoryzacja polega na przekształceniu równania do postaci iloczynowej.
- Uzupełnianie kwadratu to technika, która przekształca równanie w łatwiejszą do analizy formę.
- Wzór kwadratowy to uniwersalna metoda, która zawsze działa dla równań kwadratowych.
- Znajomość delty pozwala na szybką ocenę liczby rozwiązań: jedno, dwa lub brak rozwiązań.
- Unikanie typowych błędów, takich jak błędne obliczenia, jest kluczowe dla poprawnego rozwiązania równań.
Jak rozwiązać równanie kwadratowe - proste metody krok po kroku
Równania kwadratowe to istotny temat w matematyce, który każdy uczeń powinien zrozumieć. Równanie kwadratowe ma postać ax² + bx + c = 0, gdzie a jest różne od zera. Tego rodzaju równanie charakteryzuje się tym, że najwyższa potęga zmiennej x wynosi 2, co oznacza, że jego wykres ma formę parabolę. Zrozumienie struktury równania kwadratowego jest kluczowe dla dalszych kroków w jego rozwiązywaniu.
Aby skutecznie rozwiązać równanie kwadratowe, ważne jest zidentyfikowanie jego współczynników, które są oznaczane jako a, b i c. Współczynnik a to liczba przy x², b to liczba przy x, a c to wyraz wolny. Wartości te można łatwo odczytać z równania, co jest pierwszym krokiem do jego rozwiązania. Zrozumienie, jak zidentyfikować te współczynniki, jest fundamentalne, ponieważ stanowią one podstawę do dalszych obliczeń, takich jak obliczanie delty czy korzystanie z wzoru kwadratowego.
Zrozumienie równania kwadratowego - definicja i struktura
Równanie kwadratowe to równanie, które można zapisać w standardowej formie ax² + bx + c = 0. W tej formie a, b oraz c są stałymi, gdzie a nie może być równe zero. Równania kwadratowe mają różne zastosowania w matematyce oraz w różnych dziedzinach nauki, takich jak fizyka czy inżynieria. Ich rozwiązania mogą być przedstawione jako liczby rzeczywiste lub zespolone, w zależności od wartości delty.
Ustalanie współczynników - jak zidentyfikować a, b, c
Aby zidentyfikować współczynniki a, b i c w równaniu kwadratowym, należy je przeanalizować w kontekście ich postaci. Współczynnik a to liczba przed x², b to liczba przed x, a c to liczba, która nie zawiera zmiennej x. Na przykład, w równaniu 2x² + 3x - 5 = 0, a wynosi 2, b to 3, a c to -5. Zrozumienie tych wartości jest kluczowe dla dalszego rozwiązywania równań kwadratowych.
Metody rozwiązywania równania kwadratowego - różne podejścia
Rozwiązywanie równań kwadratowych można przeprowadzić na kilka sposobów. Wśród najpopularniejszych metod znajdują się faktoryzacja, uzupełnianie kwadratu oraz korzystanie z wzoru kwadratowego. Każda z tych metod ma swoje zalety i jest przydatna w różnych sytuacjach. Wybór odpowiedniej metody zależy od konkretnego równania oraz tego, jakie informacje są dostępne.
W dalszej części artykułu szczegółowo omówimy każdą z wymienionych metod. Zaczniemy od faktoryzacji, która polega na przekształceniu równania do postaci iloczynowej. Następnie przedstawimy technikę uzupełniania kwadratu, a na końcu zaprezentujemy wzór kwadratowy, który jest uniwersalnym narzędziem do rozwiązywania tego typu równań. Każda z tych metod pozwoli na efektywne znalezienie pierwiastków równania kwadratowego.
Rozwiązywanie przez faktoryzację - krok po kroku
Faktoryzacja to jedna z najprostszych metod rozwiązywania równań kwadratowych. Polega ona na przekształceniu równania do postaci iloczynowej, co pozwala na łatwe wyznaczenie pierwiastków. Aby zastosować tę metodę, należy znaleźć takie liczby, które po pomnożeniu dadzą wyraz wolny c, a po zsumowaniu współczynnik b. Gdy równanie jest już zapisane w postaci iloczynowej, można łatwo wyznaczyć wartości zmiennej x.
- Przekształć równanie kwadratowe do postaci iloczynowej.
- Znajdź liczby, które spełniają warunki dotyczące współczynników.
- Rozwiąż równanie, przyrównując każdy czynnik do zera.
Na przykład, dla równania x² - 5x + 6 = 0, możemy zapisać je jako (x - 2)(x - 3) = 0. Następnie, rozwiązując każde z równań x - 2 = 0 oraz x - 3 = 0, otrzymujemy pierwiastki x = 2 oraz x = 3.
Uzupełnianie kwadratu - technika i przykłady
Uzupełnianie kwadratu to technika, która pozwala na przekształcenie równania kwadratowego w formę, która ułatwia znalezienie pierwiastków. Metoda ta polega na dodaniu i odjęciu odpowiedniej liczby, aby utworzyć pełny kwadrat. Dzięki temu równanie można zapisać w postaci (x - p)² = q, co umożliwia łatwe wyznaczenie wartości zmiennej x.
Na przykład, dla równania x² - 4x - 5 = 0, możemy dodać i odjąć 4, aby uzyskać (x - 2)² - 9 = 0. Następnie przekształcamy to do postaci (x - 2)² = 9, co pozwala na łatwe obliczenie pierwiastków: x - 2 = ±3, co daje x = 5 lub x = -1.
| Metoda | Opis |
| Faktoryzacja | Przekształcenie równania do postaci iloczynowej. |
| Uzupełnianie kwadratu | Przekształcenie równania w formę pełnego kwadratu. |
| Wzór kwadratowy | Użycie wzoru x = (-b ± √Δ) / (2a) do obliczenia pierwiastków. |
Wzór kwadratowy - zastosowanie i obliczenia
Wzór kwadratowy to jedna z najważniejszych metod rozwiązywania równań kwadratowych. Jest on wyrażony jako x = (-b ± √Δ) / (2a), gdzie Δ to delta, obliczana jako Δ = b² - 4ac. Wzór ten pozwala na szybkie i efektywne znajdowanie pierwiastków równania kwadratowego bez konieczności przekształcania go w postać iloczynową. Dzięki temu, nawet w przypadku trudnych równań, można łatwo obliczyć wartości zmiennej x.
W praktyce, aby skorzystać z wzoru kwadratowego, najpierw należy obliczyć deltę. Po jej wyznaczeniu, podstawia się wartości współczynników a, b oraz c do wzoru. Na przykład, w równaniu 2x² + 4x - 6 = 0, mamy a = 2, b = 4, c = -6. Obliczamy deltę: Δ = 4² - 4 * 2 * (-6) = 16 + 48 = 64. Następnie podstawiamy do wzoru kwadratowego, co pozwala na znalezienie pierwiastków równania.
Czytaj więcej: Co zrobić gdy dziecko nie chce chodzić do szkoły: 5 skutecznych porad
Delta w równaniach kwadratowych - znaczenie i interpretacja
Delta, oznaczana jako Δ, to kluczowy element w analizie równań kwadratowych. Jej wartość decyduje o liczbie i rodzaju rozwiązań równania. Jeśli Δ > 0, równanie ma dwa różne pierwiastki rzeczywiste. Gdy Δ = 0, istnieje jeden podwójny pierwiastek, a w przypadku Δ < 0, równanie nie ma rozwiązań rzeczywistych, lecz dwa rozwiązania zespolone. Zrozumienie roli delty jest niezbędne dla efektywnego rozwiązywania równań kwadratowych.
Obliczanie delty - jak to zrobić poprawnie
Aby obliczyć deltę dla równania kwadratowego, należy skorzystać ze wzoru Δ = b² - 4ac. Wartości współczynników a, b i c można bezpośrednio odczytać z równania w postaci ax² + bx + c = 0. Na przykład, w równaniu 3x² - 12x + 9 = 0, mamy a = 3, b = -12, c = 9. Podstawiając te wartości do wzoru, otrzymujemy Δ = (-12)² - 4 * 3 * 9 = 144 - 108 = 36. Tak obliczona delta pozwala na dalsze analizy i wyznaczanie pierwiastków równania.
Interpretacja delty - liczba rozwiązań i ich rodzaj
Wartość delty (Δ) ma kluczowe znaczenie w kontekście równań kwadratowych, ponieważ determinuje liczbę i rodzaj ich rozwiązań. Kiedy Δ > 0, oznacza to, że równanie ma dwa różne pierwiastki rzeczywiste. Z kolei, gdy Δ = 0, istnieje jeden pierwiastek, zwany pierwiastkiem podwójnym. W sytuacji, gdy Δ < 0, równanie nie ma rozwiązań rzeczywistych, co oznacza, że jego rozwiązania są zespolone. Zrozumienie tych zależności jest kluczowe dla analizy równań kwadratowych.
Interpretacja delty pozwala również na lepsze zrozumienie kształtu paraboli, która reprezentuje równanie kwadratowe na wykresie. W przypadku, gdy delta jest dodatnia, parabola przecina oś x w dwóch punktach. Gdy delta jest równa zero, parabola styka się z osią x w jednym punkcie. Natomiast, gdy delta jest ujemna, parabola nie przecina osi x w ogóle. Te informacje są niezwykle przydatne w kontekście zastosowań równań kwadratowych w różnych dziedzinach, takich jak fizyka czy inżynieria.
Praktyczne przykłady równania kwadratowego - zastosowanie metod
W tej części artykułu przedstawimy kilka praktycznych przykładów ilustrujących różne metody rozwiązywania równań kwadratowych. Zastosujemy wcześniej omówione techniki, takie jak faktoryzacja, uzupełnianie kwadratu oraz wzór kwadratowy. Każdy z przykładów będzie zawierał konkretne równanie oraz kroki, które prowadzą do jego rozwiązania. Dzięki tym przykładom czytelnicy będą mogli lepiej zrozumieć, jak stosować różne metody w praktyce.
Przykład 2 - uzupełnianie kwadratu w działaniu
Rozważmy równanie kwadratowe x² + 6x + 5 = 0. Aby rozwiązać to równanie metodą uzupełniania kwadratu, zaczynamy od przekształcenia równania w formę, która umożliwi nam łatwe wyznaczenie pierwiastków. Najpierw dodajemy i odejmujemy 9 (czyli (6/2)²), aby utworzyć pełny kwadrat. Otrzymujemy więc: x² + 6x + 9 - 9 + 5 = 0, co upraszcza się do (x + 3)² - 4 = 0.
Następnie przekształcamy równanie do postaci (x + 3)² = 4. Teraz możemy wyznaczyć pierwiastki, przyrównując każdy składnik do zera. Z tego równania mamy x + 3 = ±2, co prowadzi do dwóch rozwiązań: x = -1 oraz x = -5. Dzięki metodzie uzupełniania kwadratu, udało nam się znaleźć pierwiastki równania kwadratowego w prosty sposób.
Przykład 3 - zastosowanie wzoru kwadratowego w przykładzie
Rozważmy teraz równanie kwadratowe 2x² - 4x - 6 = 0. Aby użyć wzoru kwadratowego, najpierw identyfikujemy współczynniki: a = 2, b = -4, c = -6. Obliczamy deltę: Δ = b² - 4ac = (-4)² - 4 * 2 * (-6) = 16 + 48 = 64. Ponieważ delta jest większa od zera, równanie ma dwa różne pierwiastki rzeczywiste.
Podstawiamy wartości do wzoru kwadratowego: x = (-b ± √Δ) / (2a). W naszym przypadku będzie to x = (4 ± √64) / (4), co daje x = (4 ± 8) / 4. Otrzymujemy dwa rozwiązania: x = 3 oraz x = -1. Dzięki zastosowaniu wzoru kwadratowego, szybko i efektywnie znaleźliśmy pierwiastki równania kwadratowego.
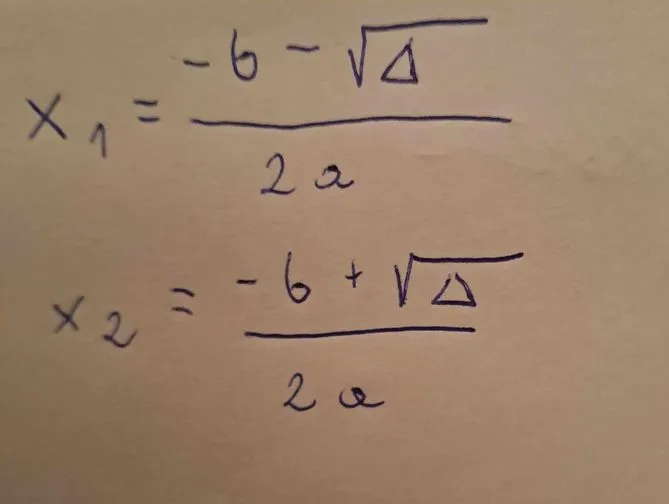
Błędy w rozwiązywaniu równań kwadratowych - jak ich unikać
Podczas rozwiązywania równań kwadratowych, wiele osób popełnia typowe błędy, które mogą prowadzić do błędnych wyników. Ważne jest, aby być szczególnie ostrożnym przy obliczaniu delty oraz przy stosowaniu wzoru kwadratowego. Często zdarza się, że pomijane są znaki przy współczynniku b lub przy obliczeniach delty.
Innym częstym błędem jest niepoprawne przekształcanie równania podczas faktoryzacji lub uzupełniania kwadratu. Niezrozumienie, jak poprawnie przekształcić równanie, może prowadzić do błędnych pierwiastków. Aby uniknąć tych problemów, warto dokładnie sprawdzać każdy krok oraz, jeśli to możliwe, korzystać z różnych metod rozwiązania równania, aby upewnić się, że wyniki są spójne.
Jak wykorzystać równania kwadratowe w codziennym życiu
Równania kwadratowe nie tylko mają zastosowanie w matematyce, ale również w wielu dziedzinach życia codziennego oraz w różnych branżach. Na przykład, inżynierowie używają równań kwadratowych do modelowania trajektorii obiektów, takich jak pojazdy czy projekty architektoniczne. Dzięki zrozumieniu, jak obliczać pierwiastki równań kwadratowych, można przewidywać, jak obiekty będą się poruszać w przestrzeni, co jest kluczowe w projektowaniu bezpiecznych i efektywnych struktur.
Warto również zauważyć, że umiejętność rozwiązywania równań kwadratowych jest przydatna w finansach. Na przykład, można je zastosować do analizy kosztów i zysków w inwestycjach, gdzie różne scenariusze mogą być modelowane jako równania kwadratowe. Zrozumienie, jak zmiany w różnych współczynnikach wpływają na wyniki, może pomóc w podejmowaniu lepszych decyzji finansowych. Dlatego znajomość równań kwadratowych otwiera drzwi do wielu praktycznych zastosowań w życiu codziennym oraz w karierze zawodowej.
