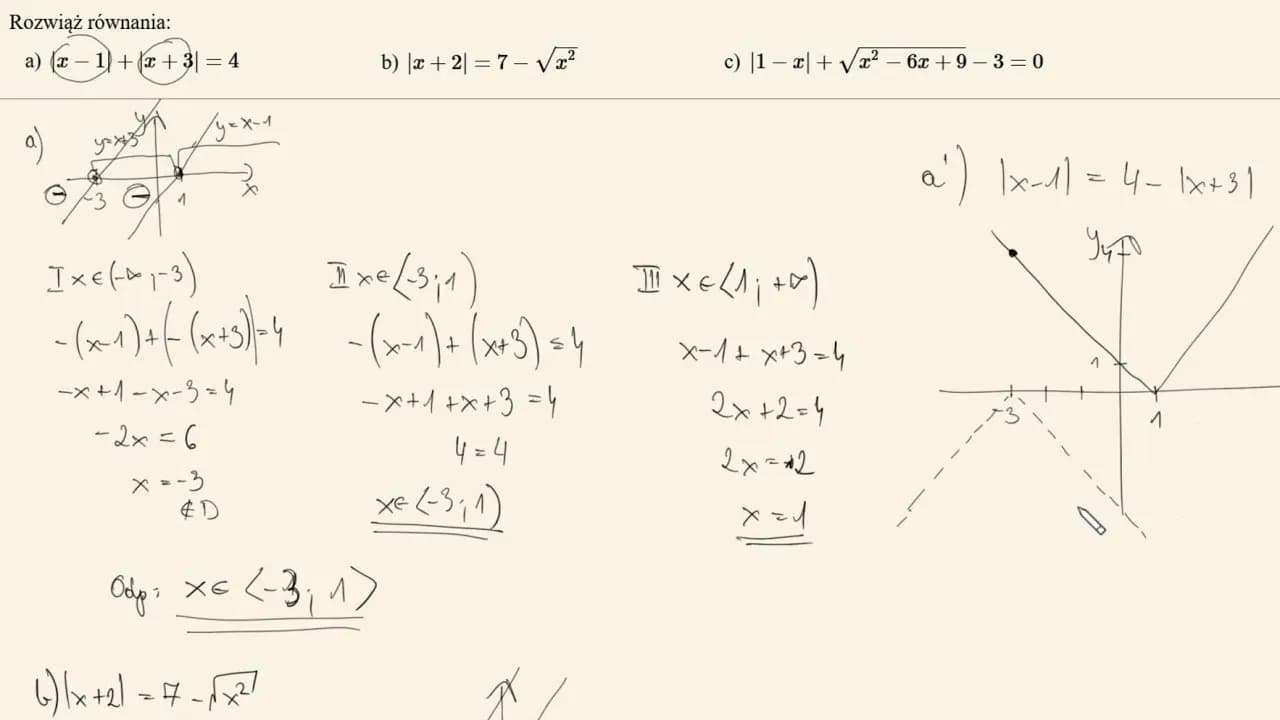Rozwiązywanie równań z wartością bezwzględną może wydawać się skomplikowane, ale z odpowiednim podejściem staje się znacznie prostsze. Wartość bezwzględna to miara odległości liczby od zera na osi liczbowej, co oznacza, że zawsze jest ona dodatnia lub równa zeru. Aby rozwiązać równanie z wartością bezwzględną, należy rozważyć dwa przypadki: pierwszy, kiedy wyrażenie wewnątrz wartości bezwzględnej jest dodatnie lub równe zeru, oraz drugi, kiedy jest ujemne.
W obu przypadkach opuszczamy znak wartości bezwzględnej, a w przypadku ujemnym dodajemy znak minus przed wyrażeniem po prawej stronie równania. W tym artykule przedstawimy krok po kroku, jak skutecznie rozwiązywać równania z wartością bezwzględną, a także omówimy najczęstsze błędy, których należy unikać.
Kluczowe informacje:- Równania z wartością bezwzględną wymagają rozważenia dwóch przypadków: dodatniego i ujemnego.
- W przypadku dodatnim opuszczamy znak wartości bezwzględnej i rozwiązujemy równanie normalnie.
- W przypadku ujemnym dodajemy znak minus przed wyrażeniem po prawej stronie równania.
- Najczęstsze błędy to ignorowanie obu przypadków oraz niepoprawne przekształcenie równań.
- Praktyczne zadania pomogą w utrwaleniu umiejętności rozwiązywania równań z wartością bezwzględną.
Jak rozwiązać równanie z wartością bezwzględną - krok po kroku
Równania z wartością bezwzględną to szczególny typ równań, które wymagają zrozumienia, jak działa wartość bezwzględna. Wartość bezwzględna liczby to jej odległość od zera na osi liczbowej, co oznacza, że zawsze przyjmuje wartość dodatnią lub zerową. Aby rozwiązać równanie z wartością bezwzględną, należy najpierw zidentyfikować, czy wyrażenie wewnątrz wartości bezwzględnej jest dodatnie, równe zeru, czy ujemne.
W przypadku, gdy wyrażenie jest dodatnie lub równe zeru, równanie można rozwiązać bezpośrednio, opuszczając znak wartości bezwzględnej. Natomiast gdy wyrażenie jest ujemne, konieczne jest dodanie znaku minus przed wyrażeniem po prawej stronie równania. Kluczowe jest zrozumienie tych zasad, ponieważ błędne podejście do wartości bezwzględnej może prowadzić do niewłaściwych rozwiązań.
Rozpoznawanie równań z wartością bezwzględną - kluczowe zasady
Aby skutecznie rozwiązywać równania z wartością bezwzględną, należy najpierw nauczyć się je rozpoznawać. Równania te zazwyczaj mają postać |ax + b| = c, gdzie a, b i c są liczbami rzeczywistymi. Kluczowe zasady obejmują:
- Wartość bezwzględna zawsze jest >= 0.
- Równanie może mieć dwa rozwiązania: jedno dla przypadku dodatniego i drugie dla przypadku ujemnego.
- Wartość bezwzględna jest używana do wyrażenia odległości, co jest istotne w kontekście równań.
Przykład 1: Rozwiązywanie równania z wartością bezwzględną - przypadek dodatni
Rozwiązywanie równań z wartością bezwzględną w przypadku, gdy wyrażenie wewnątrz wartości bezwzględnej jest dodatnie lub równe zeru, jest stosunkowo proste. Załóżmy, że mamy równanie w postaci |x + 3| = 5. W tym przypadku, ponieważ wyrażenie x + 3 jest dodatnie, możemy usunąć znak wartości bezwzględnej i przekształcić równanie na x + 3 = 5.
Następnie, aby znaleźć wartość x, odejmujemy 3 od obu stron równania. Otrzymujemy x = 5 - 3, co daje nam x = 2. Wartość ta jest jednym z rozwiązań równania. Warto również zauważyć, że w przypadku, gdyby wyrażenie było równe zeru, również moglibyśmy je usunąć, a równanie pozostałoby takie samo.
- Rozpocznij od równania w postaci |ax + b| = c.
- Jeśli wyrażenie wewnątrz wartości bezwzględnej jest dodatnie, usuń znak wartości bezwzględnej.
- Rozwiąż równanie normalnie, przekształcając je do postaci ax + b = c.
- Znajdź wartość x, a następnie sprawdź, czy spełnia oryginalne równanie.
Czytaj więcej: Ile lat po szkole możesz zdawać maturę - kompletny poradnik dla absolwenta
Najczęstsze błędy przy rozwiązywaniu równań z wartością bezwzględną - jak ich uniknąć
Rozwiązywanie równań z wartością bezwzględną może być wyzwaniem, zwłaszcza gdy popełniamy typowe błędy. Jednym z najczęstszych problemów jest ignorowanie obu przypadków wartości bezwzględnej. Kiedy rozwiązujemy równanie, musimy zawsze brać pod uwagę zarówno sytuację, gdy wyrażenie wewnątrz wartości bezwzględnej jest dodatnie, jak i wtedy, gdy jest ujemne. Pominięcie jednego z tych przypadków może prowadzić do błędnych wyników.
Ważne jest, aby pamiętać, że równania z wartością bezwzględną mogą mieć dwa różne rozwiązania. Ignorując jeden z przypadków, tracimy możliwość znalezienia wszystkich możliwych wartości x. To z kolei wpływa na naszą zdolność do rozwiązywania bardziej złożonych równań w przyszłości. Dlatego tak istotne jest, aby przy każdym równaniu z wartością bezwzględną dokładnie analizować oba przypadki.
Błąd 1: Ignorowanie obu przypadków wartości bezwzględnej
Nieprzemyślane podejście do równań z wartością bezwzględną, które polega na rozważaniu tylko jednego przypadku, jest powszechnym błędem. Taki błąd może wynikać z pośpiechu lub braku zrozumienia, jak działa wartość bezwzględna. Aby uniknąć tego problemu, zawsze upewnij się, że przetestowałeś oba przypadki, nawet jeśli jeden z nich wydaje się oczywisty.
- Przy każdym równaniu z wartością bezwzględną rozważ oba przypadki: dodatni i ujemny.
- Sprawdź, czy rozwiązanie spełnia oryginalne równanie, aby upewnić się, że nie pominąłeś żadnego przypadku.
- Dokumentuj swoje kroki, aby móc wrócić do analizy, jeśli coś pójdzie nie tak.
Błąd 2: Niepoprawne przekształcenie równań - na co zwrócić uwagę
Podczas rozwiązywania równań z wartością bezwzględną często popełnia się błędy związane z niepoprawnym przekształceniem równań. Jednym z najczęstszych problemów jest niewłaściwe zmienianie znaków lub błędna interpretacja równań. Na przykład, gdy mamy równanie |x - 2| = 3, niektórzy mogą pomylić się i zapisać x - 2 = -3, co prowadzi do błędnych wyników.
Ważne jest, aby zawsze pamiętać, że przekształcenia muszą być logiczne i zgodne z zasadami matematycznymi. Zmiana znaku przed wyrażeniem wewnątrz wartości bezwzględnej powinna być stosowana tylko wtedy, gdy rozważamy przypadek, w którym wyrażenie to jest ujemne. Ignorowanie tej zasady może prowadzić do pomyłek i nieprawidłowych rozwiązań. Kluczowe jest zrozumienie, jak działa wartość bezwzględna, aby unikać tych pułapek.
- Dokładnie przemyśl każde przekształcenie – upewnij się, że zmiany znaków są uzasadnione.
- Pracuj na równaniach krok po kroku, aby zminimalizować ryzyko błędów.
- Sprawdzaj swoje rozwiązania, podstawiając je z powrotem do oryginalnych równań.
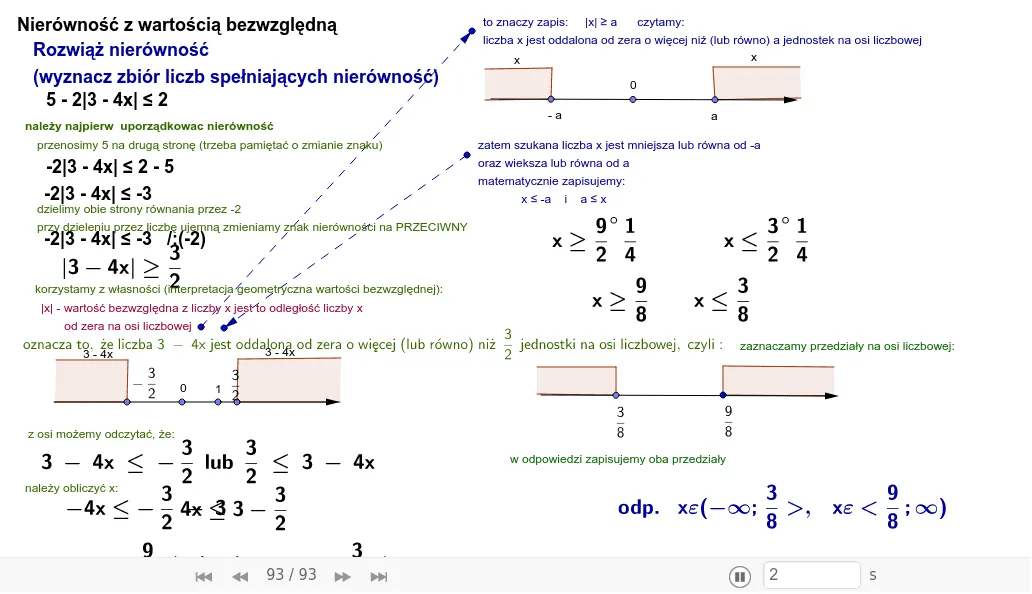
Praktyczne zadania do samodzielnego rozwiązania - sprawdź swoje umiejętności
Zadanie 1: Równanie z wartością bezwzględną do samodzielnego rozwiązania
Spróbuj rozwiązać poniższe równanie z wartością bezwzględną: |2x - 4| = 6. Aby podejść do tego zadania, pamiętaj, że musisz rozważyć dwa przypadki. W pierwszym przypadku, gdy wyrażenie wewnątrz wartości bezwzględnej jest dodatnie, możesz usunąć znak wartości bezwzględnej bez zmian. W drugim przypadku, gdy wyrażenie jest ujemne, musisz dodać znak minus przed wyrażeniem po prawej stronie równania.
Podczas rozwiązywania tego równania, upewnij się, że sprawdzasz swoje rozwiązania, podstawiając je z powrotem do oryginalnego równania. To pomoże ci upewnić się, że nie popełniłeś żadnych błędów w obliczeniach.
Zadanie 2: Równanie z wartością bezwzględną z dodatkowymi trudnościami
Teraz spróbuj rozwiązać bardziej złożone równanie: |3x + 1| - 5 = 0. W tym przypadku najpierw przekształć równanie, aby uprościć je do formy wartości bezwzględnej. Następnie ponownie rozważ oba przypadki: dodatni i ujemny, aby znaleźć wszystkie możliwe rozwiązania. Pamiętaj, aby zwrócić uwagę na znaki i dokładnie przemyśleć, co dzieje się z równaniem w każdym przypadku.
Rozwiązywanie równań z wartością bezwzględną może być wyzwaniem, ale praktyka pomoże ci w opanowaniu tej umiejętności. Upewnij się, że przeanalizowałeś wszystkie kroki, aby uniknąć typowych błędów.
Jak wykorzystać równania z wartością bezwzględną w codziennym życiu
Równania z wartością bezwzględną nie tylko mają zastosowanie w matematyce akademickiej, ale również w wielu praktycznych sytuacjach w życiu codziennym. Na przykład, mogą być używane do obliczania odległości w różnych kontekstach, takich jak planowanie tras podróży czy analiza danych dotyczących ruchu drogowego. Kiedy rozważasz różne scenariusze, w których musisz uwzględnić zmiany w kierunku, równania z wartością bezwzględną pomogą ci zrozumieć, jak daleko jesteś od celu, niezależnie od kierunku, w którym się poruszasz.
Dodatkowo, w kontekście finansowym, równania te mogą być używane do analizy ryzyka inwestycyjnego. Na przykład, inwestorzy mogą korzystać z wartości bezwzględnej do obliczania odchyleń od oczekiwanych wyników, co pozwala im lepiej zrozumieć potencjalne straty lub zyski. Zrozumienie, jak stosować metody rozwiązywania równań z wartością bezwzględną w praktycznych sytuacjach, może znacząco wpłynąć na twoje umiejętności analityczne i podejmowanie decyzji w codziennym życiu.
