Liczby, których wartość bezwzględna jest równa 4, to temat, który może wydawać się skomplikowany, ale w rzeczywistości jest bardzo prosty. Wartość bezwzględna liczby to jej odległość od zera na osi liczbowej, niezależnie od kierunku. Dla liczby 4 oraz -4, ta odległość wynosi dokładnie 4 jednostki. Zapis matematyczny dla tych liczb to $$|-4| = 4$$ oraz $$|4| = 4$$.
W artykule przyjrzymy się bliżej, co oznacza wartość bezwzględna, jakie liczby ją reprezentują oraz jakie ma znaczenie w matematyce i codziennym życiu. Zrozumienie tego konceptu pozwala lepiej operować na liczbach i ich różnicach, co jest niezwykle przydatne w różnych sytuacjach.
Kluczowe wnioski:- Wartość bezwzględna liczby to jej odległość od zera na osi liczbowej.
- Liczby -4 i 4 mają wartość bezwzględną równą 4.
- Wartość bezwzględna jest użyteczna w wielu kontekstach matematycznych i codziennych.
- Można ją wizualizować na osi liczbowej, co ułatwia zrozumienie jej zastosowania.

Liczby o wartości bezwzględnej równej 4 – definicja i przykłady
Wartość bezwzględna liczby to jej odległość od zera na osi liczbowej, niezależnie od kierunku. Oznacza to, że dla każdej liczby, wartość bezwzględna jest zawsze liczbą nieujemną. W przypadku liczb, których wartość bezwzględna jest równa 4, mamy do czynienia z dwoma konkretnymi przykładami: 4 oraz -4. Obie te liczby mają tę samą odległość od zera, co czyni je równymi pod względem wartości bezwzględnej.Matematycznie zapisujemy to jako $$|-4| = 4$$ oraz $$|4| = 4$$. Wartość bezwzględna jest istotnym pojęciem w matematyce, które pomaga w zrozumieniu różnorodnych operacji na liczbach. W kolejnych sekcjach przyjrzymy się bliżej, jakie liczby mają wartość bezwzględną równą 4 oraz jakie mają one właściwości.
Zrozumienie wartości bezwzględnej – co to oznacza?
Wartość bezwzględna to fundamentalny koncept w matematyce, który odnosi się do odległości liczby od zera. Oblicza się ją poprzez usunięcie znaku minus z liczby, jeśli jest obecny. Na przykład, dla liczby -4, wartość bezwzględna wynosi 4, ponieważ odległość od zera na osi liczbowej wynosi 4 jednostki. Podobnie, dla liczby 4, wartość bezwzględna również wynosi 4.
Wartość bezwzględna ma kilka ważnych właściwości. Po pierwsze, jest zawsze nieujemna, co oznacza, że nigdy nie przyjmuje wartości ujemnych. Po drugie, dla każdej liczby x, wartość bezwzględna jest równa wartości bezwzględnej liczby -x. To sprawia, że pojęcie to jest niezwykle użyteczne w różnych kontekstach matematycznych i praktycznych.
Przykłady liczb – które liczby mają wartość bezwzględną 4?
Liczby, których wartość bezwzględna jest równa 4, to -4 oraz 4. Oba te przypadki ilustrują, jak wartość bezwzględna działa w praktyce. Wartość bezwzględna to odległość liczby od zera na osi liczbowej, a w tym przypadku wynosi ona 4 jednostki. Zapis matematyczny tych liczb to $$|-4| = 4$$ oraz $$|4| = 4$$. Oznacza to, że zarówno liczba 4, jak i liczba -4, mają tę samą wartość bezwzględną, co czyni je doskonałymi przykładami.
- -4
- 4
Wartość bezwzględna w matematyce – dlaczego jest ważna?
Wartość bezwzględna odgrywa kluczową rolę w matematyce, ponieważ pozwala na zrozumienie i porównywanie liczb w sposób, który nie zależy od ich znaku. Jest to szczególnie istotne w operacjach matematycznych, takich jak dodawanie, odejmowanie czy rozwiązywanie równań. Dzięki temu, że wartość bezwzględna zawsze daje wynik nieujemny, możemy łatwiej analizować różnice między liczbami, a także zrozumieć pojęcia takie jak odległość czy różnice temperatur.
W codziennym życiu wartość bezwzględna znajduje zastosowanie w wielu sytuacjach. Na przykład, w pomiarach odległości, różnic temperatur czy w finansach, gdzie zyski i straty mogą być przedstawiane jako wartości bezwzględne. Pozwala to na lepsze zrozumienie sytuacji bez względu na to, czy mamy do czynienia z wartościami dodatnimi, czy ujemnymi. Dlatego znajomość wartości bezwzględnej jest niezbędna w różnych dziedzinach matematyki i nauk przyrodniczych.
Zastosowanie wartości bezwzględnej w codziennym życiu
Wartość bezwzględna ma wiele praktycznych zastosowań w codziennym życiu. Na przykład, w pomiarze odległości, wartość bezwzględna pozwala na określenie, jak daleko znajduje się obiekt od punktu odniesienia, niezależnie od kierunku. W pomiarach temperatury, różnice między temperaturami mogą być wyrażane jako wartości bezwzględne, co ułatwia zrozumienie, jak bardzo zmienia się temperatura, niezależnie od tego, czy jest ona dodatnia, czy ujemna. Wreszcie, w finansach, wartość bezwzględna jest używana do obliczania zysków i strat, co pozwala na lepsze zarządzanie budżetem i analizowanie sytuacji finansowych.
- Pomiary odległości: Umożliwiają określenie, jak daleko znajduje się obiekt od innego punktu.
- Pomiary temperatury: Ułatwiają analizę różnic temperatur, niezależnie od ich znaku.
- Finanse: Pomagają w obliczaniu zysków i strat, co jest kluczowe w zarządzaniu budżetem.
Wartość bezwzględna a różnice – jak to działa?
Wartość bezwzględna jest kluczowym narzędziem w obliczaniu różnic między liczbami. Gdy mówimy o różnicy między dwiema liczbami, często interesuje nas, jak daleko one od siebie są, niezależnie od kierunku. W tym kontekście wartość bezwzględna pozwala nam uzyskać liczbę nieujemną, która reprezentuje tę odległość. Na przykład, jeśli mamy liczby 3 i -1, różnica między nimi wynosi 4, co możemy zapisać jako |3 - (-1)| = |3 + 1| = |4| = 4. Dzięki temu, wartość bezwzględna umożliwia nam zrozumienie, jak duże są różnice między wartościami, bez względu na ich znaki.
Użycie wartości bezwzględnej w obliczeniach różnic jest szczególnie istotne w różnych dziedzinach, takich jak matematyka, statystyka czy nawet w życiu codziennym. Pozwala to na analizowanie danych i podejmowanie decyzji opartych na rzeczywistych różnicach, a nie tylko na ich wartościach. W praktyce, wartość bezwzględna pomaga również w analizie zmian, co jest niezwykle przydatne w kontekście finansów czy nauk przyrodniczych.
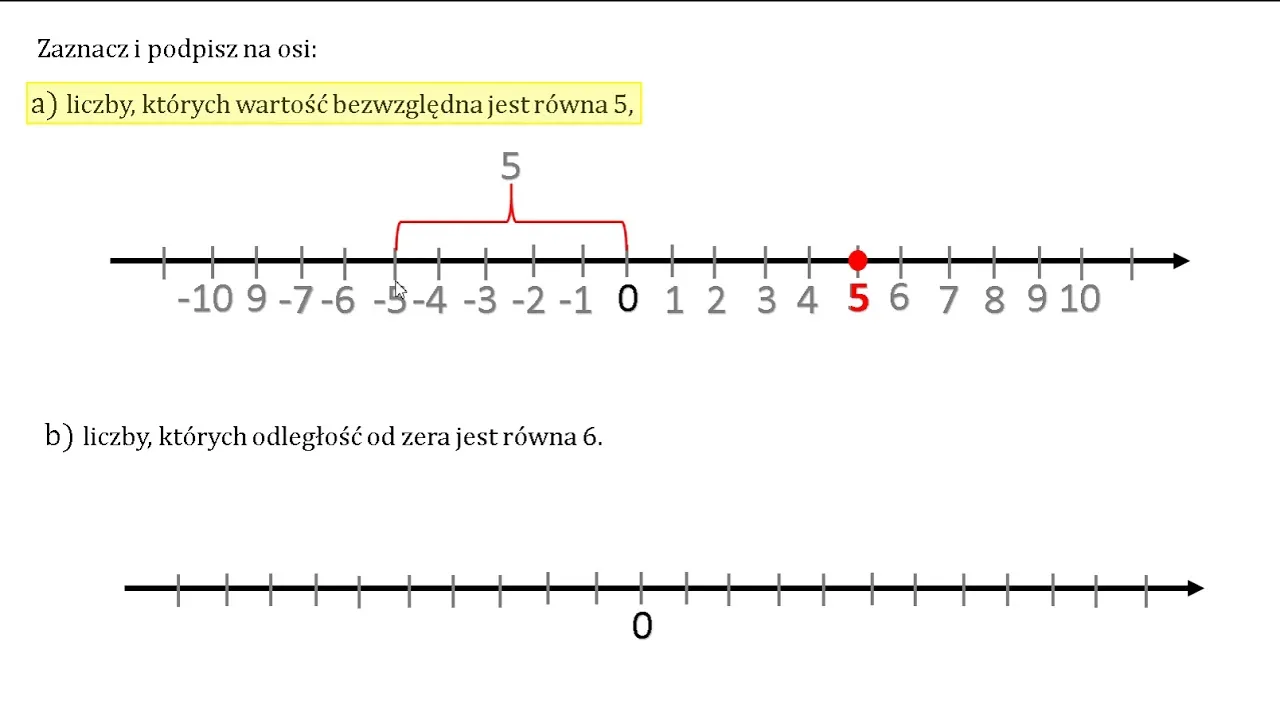
Wizualizacja wartości bezwzględnej – jak używać osi liczbowej?
Oś liczbowa to narzędzie, które pozwala na wizualizację wartości liczb i ich relacji. Na osi liczbowej każda liczba ma swoje miejsce, co ułatwia zrozumienie, jak są one rozmieszczone w stosunku do siebie. Wartość bezwzględna liczby jest reprezentowana jako odległość tej liczby od zera. Na przykład, liczby -4 i 4 znajdują się w równych odległościach od zera, co ilustruje, że mają tę samą wartość bezwzględną, wynoszącą 4.
Aby zobrazować to na osi liczbowej, możemy zaznaczyć punkty dla każdej liczby. Oś biegnie od minus nieskończoności do plus nieskończoności, a wartości bezwzględne są zawsze przedstawiane jako odległości od zera. To podejście nie tylko ułatwia zrozumienie pojęcia wartości bezwzględnej, ale także pozwala na łatwe porównywanie liczb, co jest szczególnie przydatne w matematyce i naukach ścisłych. Wizualizacja na osi liczbowej pomaga również w dostrzeganiu wzorców i trendów w danych.
Oś liczbowa jako narzędzie do zrozumienia wartości bezwzględnej
Oś liczbowa to wizualne narzędzie, które umożliwia zrozumienie relacji między różnymi liczbami oraz ich wartościami bezwzględnymi. Na osi liczbowej liczby są rozmieszczone w sposób liniowy, co pozwala na łatwe porównywanie ich odległości od zera. Każda liczba ma swoje miejsce, a wartość bezwzględna danej liczby jest reprezentowana jako jej odległość od zera, co oznacza, że zarówno -4, jak i 4 znajdują się w tej samej odległości od zera, co ilustruje ich równą wartość bezwzględną wynoszącą 4.
Interpretując oś liczbową, można dostrzec, jak liczby dodatnie i ujemne są rozmieszczone względem siebie. Na przykład, liczby z wartością bezwzględną równą 4 (czyli -4 i 4) są umieszczone w równych odległościach po obu stronach zera. Dzięki tej wizualizacji, łatwiej zrozumieć, jak różne liczby odnoszą się do siebie i jak obliczać różnice między nimi. Oś liczbowa jest zatem nie tylko narzędziem do przedstawiania liczb, ale także do głębszego zrozumienia pojęcia wartości bezwzględnej.| Liczba | Wartość bezwzględna |
|---|---|
| -4 | 4 |
| 4 | 4 |
| -2 | 2 |
| 2 | 2 |
| -1 | 1 |
| 1 | 1 |
Praktyczne zastosowania wartości bezwzględnej w programowaniu
Wartość bezwzględna znajduje również zastosowanie w programowaniu, szczególnie w kontekście analizy danych i algorytmów. Na przykład, w algorytmach uczenia maszynowego, wartość bezwzględna jest często wykorzystywana do obliczania błędów predykcji. Użycie wartości bezwzględnej pozwala na zminimalizowanie wpływu wartości ujemnych, co ułatwia optymalizację modeli. Dzięki temu, programiści mogą skuteczniej dostosowywać swoje algorytmy, aby poprawić dokładność predykcji.
Dodatkowo, w grafice komputerowej, wartość bezwzględna jest używana do obliczeń związanych z odległością między punktami w przestrzeni 2D lub 3D. Na przykład, przy obliczaniu odległości między obiektami, wartość bezwzględna pozwala na zrozumienie, jak blisko lub daleko są one od siebie, co jest kluczowe w symulacjach i grach komputerowych. W miarę jak technologia się rozwija, znaczenie wartości bezwzględnej w programowaniu będzie tylko rosło, otwierając nowe możliwości dla innowacyjnych aplikacji.