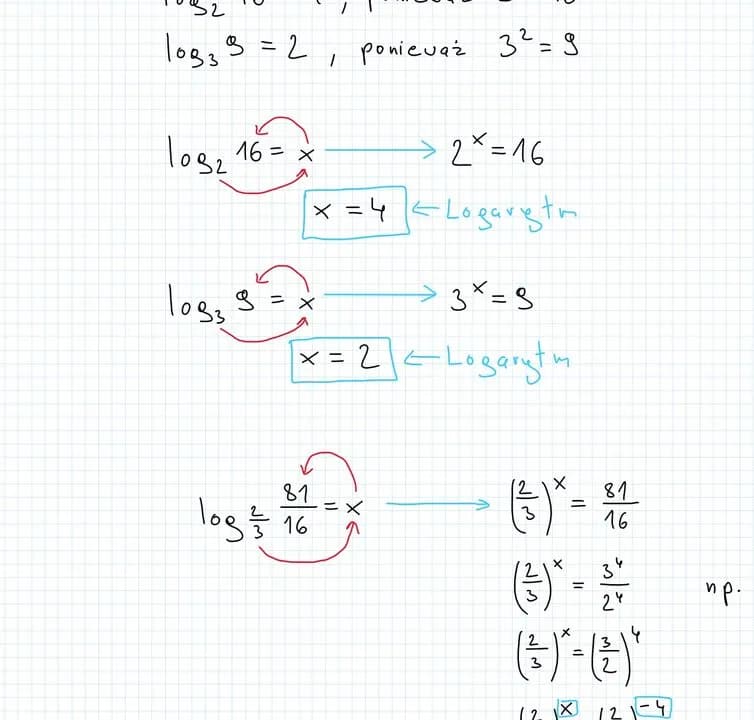
Co jeśli logarytm nie ma podstawy? To pytanie często pojawia się w matematyce, zwłaszcza w kontekście logarytmów dziesiętnych i naturalnych. Gdy logarytm nie ma podanej podstawy, domyślnie przyjmuje się, że jego podstawą jest 10. Oznacza to, że korzystamy z logarytmu dziesiętnego, który jest powszechnie stosowany w różnych dziedzinach, od finansów po nauki przyrodnicze. Inną popularną formą logarytmu bez określonej podstawy jest logarytm naturalny, oznaczany jako ln, którego podstawą jest liczba Eulera (e).
W artykule przyjrzymy się bliżej, jakie są domyślne wartości logarytmu oraz w jakich sytuacjach są one stosowane. Zrozumienie tych koncepcji jest kluczowe dla właściwego korzystania z logarytmów w praktyce, a także dla ich zastosowania w rozwiązywaniu problemów matematycznych i naukowych.
Kluczowe informacje:- Logarytm bez podanej podstawy domyślnie przyjmuje wartość 10, co oznacza logarytm dziesiętny.
- Logarytm naturalny, oznaczany jako ln, ma podstawę równą liczbie Eulera (e).
- Logarytmy są używane w różnych dziedzinach, takich jak finanse, nauki przyrodnicze i inżynieria.
- Zrozumienie podstaw logarytmu jest kluczowe dla obliczeń matematycznych i rozwiązywania równań.
- Znajomość zastosowań logarytmów może znacznie ułatwić pracę w naukach ścisłych i technicznych.
Co oznacza logarytm bez podanej podstawy i jego zastosowanie?
Logarytm bez podanej podstawy to koncept matematyczny, który ma istotne znaczenie w różnych dziedzinach. Gdy nie wskazano podstawy logarytmu, przyjmuje się, że jest to logarytm dziesiętny, co oznacza, że jego podstawą jest liczba 10. To podejście jest powszechnie stosowane w praktyce, szczególnie w obliczeniach finansowych oraz w naukach przyrodniczych. Inną formą logarytmu bez określonej podstawy jest logarytm naturalny, oznaczany jako ln, którego podstawą jest liczba Eulera (e). Zrozumienie tych pojęć jest kluczowe dla właściwego korzystania z logarytmów w matematyce i naukach ścisłych.Logarytmy odgrywają ważną rolę w modelowaniu różnych zjawisk, takich jak wzrost populacji, rozprzestrzenianie się chorób czy zmiany w finansach. Dzięki nim można łatwiej analizować i interpretować złożone dane. Warto również zauważyć, że znajomość logarytmów jest niezbędna przy rozwiązywaniu równań, co czyni je nieocenionym narzędziem w matematyce i inżynierii.
Jakie są domyślne podstawy logarytmu w matematyce?
W matematyce logarytmy mają kilka domyślnych podstaw, które są kluczowe dla ich zastosowania. Podstawą logarytmu dziesiętnego jest liczba 10, co oznacza, że logarytm dziesiętny jest najczęściej używany w codziennych obliczeniach oraz w kontekście finansowym. Z kolei logarytm naturalny ma podstawę równą liczbie Eulera (e), która wynosi około 2.71828. Logarytmy te są szeroko stosowane w różnych dziedzinach, takich jak matematyka, statystyka, inżynieria czy ekonomia.
W praktyce, wybór odpowiedniej podstawy logarytmu zależy od kontekstu, w jakim jest on używany. Logarytmy dziesiętne są preferowane w obliczeniach związanych z finansami oraz statystyką, natomiast logarytmy naturalne są kluczowe w analizie zjawisk przyrodniczych i naukowych. Dzięki tym podstawowym wartościom, logarytmy stają się narzędziem umożliwiającym zrozumienie i analizowanie złożonych problemów matematycznych.
W jakich sytuacjach używamy logarytmu dziesiętnego i naturalnego?
Logarytmy dziesiętne i naturalne znajdują zastosowanie w wielu dziedzinach życia. Logarytm dziesiętny, z podstawą 10, jest często wykorzystywany w finansach, gdzie pomaga w obliczeniach związanych z oprocentowaniem i analizą wzrostu kapitału. Na przykład, inwestorzy mogą korzystać z logarytmu dziesiętnego, aby obliczyć czas potrzebny do podwojenia inwestycji przy danym oprocentowaniu. Z kolei logarytm naturalny, oznaczany jako ln, jest powszechnie stosowany w naukach przyrodniczych, szczególnie w biologii i chemii, gdzie modeluje zjawiska takie jak rozpad radioaktywny czy wzrost populacji.
W kontekście nauk ścisłych, logarytmy są nieocenione w analizie danych. Na przykład, w statystyce logarytmy mogą pomóc w przekształceniu danych, które mają charakter eksponencjalny, na bardziej liniowy, co ułatwia ich interpretację. W inżynierii, logarytm naturalny jest często używany w równaniach dotyczących procesów dynamicznych, takich jak przepływ ciepła czy reakcje chemiczne. Dzięki tym zastosowaniom, logarytmy stają się kluczowym narzędziem w rozwiązywaniu złożonych problemów.
Jak obliczać logarytmy bez podanej podstawy?
Obliczanie logarytmów bez podanej podstawy może być proste, jeśli rozumiemy zasady, które za tym stoją. Gdy nie mamy określonej podstawy, przyjmuje się, że używamy logarytmu dziesiętnego. W praktyce oznacza to, że możemy korzystać z kalkulatorów lub programów komputerowych, które automatycznie stosują odpowiednie wzory. Na przykład, aby obliczyć logarytm liczby 100 w podstawie 10, wystarczy wpisać "log(100)", a wynik to 2, ponieważ 10 do potęgi 2 daje 100.W przypadku logarytmu naturalnego, proces jest podobny, ale używamy funkcji ln. Na przykład, aby obliczyć ln(7.39), wprowadzamy tę wartość do kalkulatora, a on zwraca wynik około 2.0. Warto pamiętać, że logarytmy mają swoje zastosowanie nie tylko w teorii, ale także w praktycznych obliczeniach, które spotykamy na co dzień.
| Podstawa | Logarytm | Wynik |
| 10 | log(100) | 2 |
| e | ln(7.39) | 2.0 |
Przykłady obliczeń logarytmów dziesiętnych i naturalnych
Obliczanie logarytmów dziesiętnych i naturalnych jest kluczowe w wielu sytuacjach praktycznych. Na przykład, aby obliczyć logarytm dziesiętny liczby 1000, możemy użyć wzoru: log(1000). Ponieważ 10 do potęgi 3 równa się 1000, wynik to 3. Innym przykładem jest obliczenie logarytmu dziesiętnego liczby 10. W tym przypadku log(10) wynosi 1, ponieważ 10 do potęgi 1 to 10.
Przechodząc do logarytmów naturalnych, weźmy na przykład liczbę 20. Aby obliczyć ln(20), korzystamy z kalkulatora, który zwraca wynik około 2.9957. To oznacza, że e do potęgi 2.9957 daje 20. Kolejnym przykładem może być ln(2.718), gdzie wynik wynosi 1, ponieważ e do potęgi 1 to właśnie e. Takie obliczenia są niezbędne w naukach przyrodniczych i inżynierii, gdzie logarytmy naturalne są często używane do modelowania różnych zjawisk.
Jak interpretować wyniki logarytmów bez określonej podstawy?
Interpretacja wyników logarytmów bez określonej podstawy jest kluczowa dla zrozumienia ich znaczenia w praktyce. Na przykład, wynik logarytmu dziesiętnego może wskazywać, ile razy musimy pomnożyć 10, aby uzyskać daną liczbę. Jeśli log(100) wynosi 2, oznacza to, że 10 do potęgi 2 daje 100. Z kolei w przypadku logarytmu naturalnego, wynik ln(7.39) wynoszący około 2.0 oznacza, że e do potęgi 2.0 daje 7.39. Zrozumienie tych wyników jest istotne w kontekście analizy danych i podejmowania decyzji opartych na tych obliczeniach.
Czytaj więcej: Do kiedy można zmienić szkołę średnią: terminy i procedura przeniesienia
Dlaczego znajomość podstaw logarytmu jest istotna w praktyce?

Znajomość podstaw logarytmu jest kluczowa w wielu dziedzinach, takich jak nauki ścisłe, inżynieria i finanse. Zrozumienie, jak działają logarytmy, pozwala na efektywne rozwiązywanie problemów i analizę danych. W kontekście naukowym, logarytmy są niezbędne w modelowaniu zjawisk, takich jak wzrost populacji czy procesy chemiczne. W inżynierii, umiejętność korzystania z logarytmów ułatwia pracę nad złożonymi równaniami i symulacjami. Dlatego znajomość tych podstaw jest nie tylko teoretyczna, ale ma również praktyczne zastosowanie w życiu codziennym i zawodowym.
Zastosowania logarytmów w naukach ścisłych i inżynierii
Logarytmy są szeroko stosowane w naukach ścisłych oraz inżynierii, gdzie pomagają w analizie i interpretacji danych. Na przykład, w akustyce logarytmy są używane do obliczania poziomów dźwięku w decybelach, co jest istotne w projektowaniu systemów audio. W chemii, logarytmy naturalne są wykorzystywane do opisu procesów reakcji chemicznych, takich jak szybkość reakcji. W inżynierii elektrycznej logarytmy pomagają w analizie obwodów oraz w obliczeniach związanych z mocą i napięciem. Dzięki tym zastosowaniom, logarytmy stają się niezbędnym narzędziem w rozwiązywaniu problemów technicznych i naukowych.Jak logarytmy wpływają na rozwiązywanie równań i problemów?
Logarytmy odgrywają kluczową rolę w rozwiązywaniu równań, szczególnie w algebra i analizie matematycznej. Umożliwiają one przekształcanie złożonych równań do prostszej formy, co ułatwia ich rozwiązanie. Na przykład, równanie 10^x = 1000 można przekształcić do postaci logarytmicznej, co daje x = log(1000). Dzięki temu możemy łatwo znaleźć wartość x, co w przeciwnym razie mogłoby być trudne.
Innym przykładem jest równanie, w którym występuje logarytm naturalny, takie jak e^x = 5. W tym przypadku używamy logarytmu naturalnego, aby przekształcić równanie do postaci x = ln(5). To przekształcenie pozwala na szybkie obliczenie wartości x. Logarytmy są więc niezwykle przydatne w uproszczeniu i rozwiązywaniu równań, co czyni je niezastąpionym narzędziem w matematyce.
- Równanie 10^x = 1000 przekształca się do x = log(1000).
- Równanie e^x = 5 przekształca się do x = ln(5).
- Logarytmy są używane do uproszczenia równań w analizie matematycznej.
Jak logarytmy wspierają analizę danych w erze big data?
W dobie big data, gdzie ilość danych rośnie w zastraszającym tempie, logarytmy stają się kluczowym narzędziem w analizie danych. Umożliwiają one przekształcanie danych o dużym zakresie wartości do bardziej zarządzalnej postaci. Przykładowo, w analizie statystycznej logarytmy mogą być używane do normalizacji danych, co pozwala na lepsze porównanie wyników i eliminację wpływu wartości odstających. Dzięki temu analitycy mogą bardziej precyzyjnie identyfikować trendy i wzorce w danych.
Co więcej, logarytmy są wykorzystywane w algorytmach uczenia maszynowego, gdzie pomagają w optymalizacji modeli predykcyjnych. Zastosowanie logarytmów w funkcjach straty umożliwia lepsze dopasowanie modeli do danych, co zwiększa ich efektywność. W miarę jak technologia i narzędzia analityczne się rozwijają, znaczenie logarytmów w analizie danych będzie tylko rosło, a ich zrozumienie stanie się niezbędne dla specjalistów w tej dziedzinie.