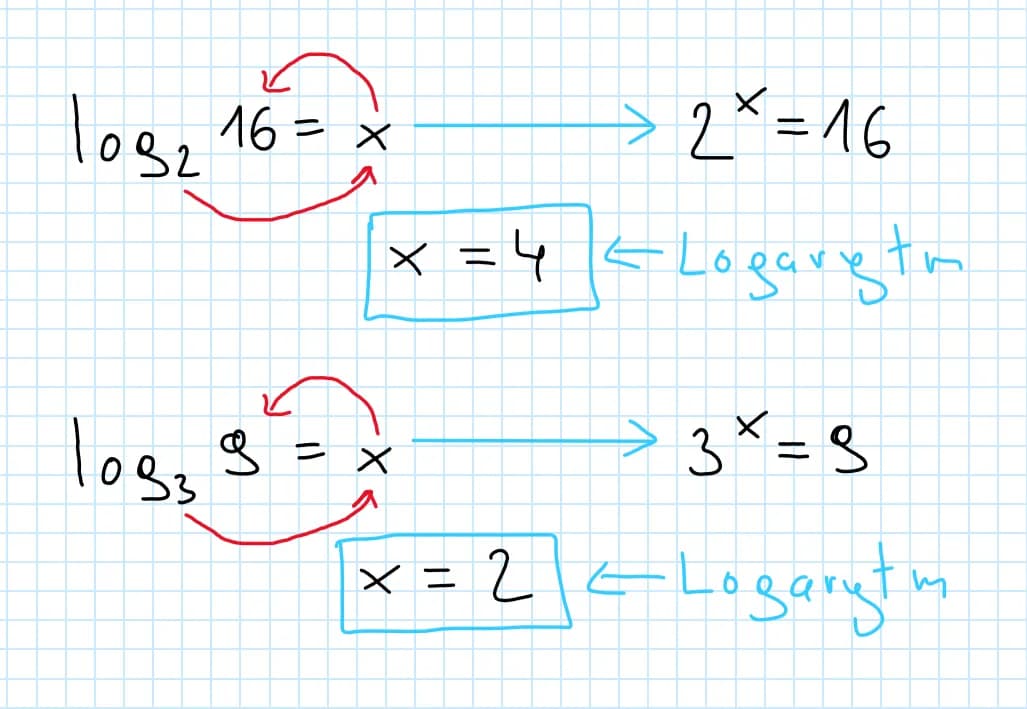W dalszej części tekstu znajdziesz praktyczne przykłady, które pomogą Ci lepiej zrozumieć temat, a także wskazówki dotyczące narzędzi i kalkulatorów, które mogą ułatwić obliczenia. Dzięki temu nauka obliczania logarytmu z ułamkiem stanie się prostsza i bardziej przystępna.
Kluczowe informacje:- Logarytm z ułamka oblicza się, znajdując liczbę, którą należy podnieść do podstawy, aby uzyskać ten ułamek.
- Logarytm jest odwrotnością operacji wykładniczej, co oznacza, że można go zastosować do różnych rodzajów ułamków.
- W artykule omówimy regułę ilorazu, która jest kluczowa przy obliczaniu logarytmów z ułamkami.
- Przedstawimy praktyczne przykłady obliczeń logarytmu z prostymi i bardziej złożonymi ułamkami.
- Znajdziesz również rekomendacje dotyczące najlepszych kalkulatorów online do obliczania logarytmów.
Jak obliczyć logarytm z ułamkiem - krok po kroku
Obliczanie logarytmu z ułamkiem może być proste, jeśli zrozumiesz kluczowe zasady tego procesu. Logarytm to sposób na wyrażenie, jaką liczbę trzeba podnieść do określonej podstawy, aby otrzymać daną wartość. W przypadku ułamków, obliczenia te wymagają zastosowania odpowiednich wzorów i zrozumienia, jak ułamki wpływają na wynik logarytmu.
Aby obliczyć logarytm z ułamkiem, należy najpierw zidentyfikować podstawę logarytmu oraz wartość, z której chcemy obliczyć logarytm. Następnie można zastosować wzór logarytmu, który pozwala na przekształcenie ułamka w bardziej zrozumiałą formę. W kolejnych krokach omówimy, jak to zrobić, aby proces był jak najbardziej przystępny.
Zrozumienie podstawowych pojęć logarytmu i ułamka
Logarytm to matematyczna operacja, która odpowiada na pytanie, ile razy musimy pomnożyć daną liczbę (podstawę) przez siebie, aby uzyskać inną liczbę. Na przykład, logarytm o podstawie 10 z liczby 1000 to 3, ponieważ 10^3 = 1000. Ułamki, z drugiej strony, to liczby, które przedstawiają część całości. W kontekście logarytmów, ułamki mogą być traktowane jako liczby, których logarytmy również można obliczać.
Ważne jest, aby zrozumieć, że logarytm z ułamka może być obliczany na podstawie właściwości logarytmów. Na przykład, logarytm z ułamka a/b można zapisać jako różnicę logarytmów: log(a) - log(b). To podejście sprawia, że obliczenia stają się prostsze i bardziej zrozumiałe, a także pozwala na łatwiejsze manipulowanie wartościami ułamków.
Jak stosować wzór logarytmu do ułamków
W obliczeniach logarytmicznych, szczególnie przy pracy z ułamkami, kluczowe jest zrozumienie, jak stosować wzór logarytmu. Logarytm z ułamka a/b można zapisać jako różnicę logarytmów: log(a) - log(b). To podejście upraszcza obliczenia i pozwala na łatwiejsze manipulowanie wartościami. Dzięki tej metodzie, można z łatwością obliczyć logarytmy z ułamków, korzystając z podstawowych właściwości logarytmów.Aby zastosować ten wzór w praktyce, należy najpierw obliczyć logarytmy liczników i mianowników osobno, a następnie je od siebie odjąć. Kluczowe jest, aby pamiętać o podstawie logarytmu, ponieważ zmienia ona wyniki obliczeń. W kolejnych krokach omówimy, jak przeprowadzić te obliczenia, aby były jak najbardziej zrozumiałe i efektywne.
Logarytm z ułamka - właściwości i zasady
Logarytmy mają wiele właściwości, które są szczególnie ważne przy pracy z ułamkami. Jedną z najistotniejszych zasad jest reguła ilorazu, która stanowi, że logarytm z ilorazu dwóch liczb jest równy różnicy logarytmów tych liczb. Dzięki tej regule, obliczenia logarytmiczne stają się znacznie prostsze, ponieważ można je rozdzielić na mniejsze, bardziej zrozumiałe części.
Reguła ilorazu jest niezwykle przydatna w przypadku ułamków, ponieważ pozwala na zapisanie logarytmu z ułamka jako różnicy logarytmu licznika i logarytmu mianownika. Ta zasada nie tylko ułatwia obliczenia, ale także umożliwia lepsze zrozumienie relacji między liczbami. Zrozumienie tych właściwości jest kluczowe dla skutecznego obliczania logarytmów z ułamkami oraz ich zastosowań w matematyce i naukach ścisłych.
Zasada dzielenia w logarytmach - reguła ilorazu
Reguła ilorazu to jedna z podstawowych zasad logarytmów, która jest niezwykle przydatna przy obliczaniu logarytmu z ułamków. Zgodnie z tą zasadą, logarytm ilorazu dwóch liczb można zapisać jako różnicę logarytmów tych liczb. Oznacza to, że log(a/b) = log(a) - log(b). Dzięki temu, obliczenia stają się prostsze, ponieważ można rozdzielić skomplikowane operacje na mniejsze, bardziej zrozumiałe kroki.
W praktyce, stosując regułę ilorazu, należy najpierw obliczyć logarytmy liczników i mianowników osobno. Następnie, wyniki te odejmujemy od siebie, aby uzyskać logarytm z ułamka. Ta zasada jest kluczowa, ponieważ pozwala na łatwiejsze manipulowanie wartościami i oszczędza czas podczas obliczeń. Zrozumienie reguły ilorazu jest fundamentalne dla każdego, kto chce efektywnie obliczać logarytmy z ułamkami.
Jak wykorzystać regułę ilorazu w praktyce
Aby zastosować regułę ilorazu w praktyce, rozważmy przykład obliczenia logarytmu z ułamka 8/2. Zgodnie z regułą, możemy zapisać to jako log(8) - log(2). Obliczając te logarytmy, otrzymujemy log(8) = 3 (ponieważ 2^3 = 8) oraz log(2) = 1. W rezultacie, log(8/2) = 3 - 1 = 2.
Wynik ten pokazuje, jak praktycznie zastosować regułę ilorazu w obliczeniach. Dzięki temu, możemy nie tylko obliczać logarytmy z ułamków, ale również lepiej zrozumieć relacje między liczbami. Warto pamiętać, że stosując tę zasadę, możemy łatwo rozwiązywać bardziej złożone problemy matematyczne, co czyni ją nieocenionym narzędziem w matematyce.
| Ułamek | Logarytm (a) | Logarytm (b) | Log(a/b) |
| 8/2 | 3 | 1 | 2 |
| 10/5 | 1 | 0.699 | 0.301 |
Czytaj więcej: Co jest po liceum? Poznaj możliwości rozwoju kariery
Przykłady obliczeń logarytmu z ułamkiem

Obliczanie logarytmu z ułamkiem może być prostsze, gdy zastosujemy odpowiednie metody. W tym przykładzie zajmiemy się logarytmem prostego ułamka, takiego jak 1/4. Aby obliczyć logarytm z tego ułamka, możemy wykorzystać regułę ilorazu: log(1/4) = log(1) - log(4). Ponieważ log(1) = 0, otrzymujemy log(1/4) = 0 - log(4). Zatem, jeśli przyjmiemy, że log(4) = 2 (przy podstawie 2), mamy log(1/4) = -2. To pokazuje, jak można łatwo obliczyć logarytm z prostego ułamka.
W kolejnym przykładzie obliczymy logarytm z bardziej złożonego ułamka, jakim jest 8/2. Korzystając z tej samej reguły ilorazu, zapisujemy to jako log(8) - log(2). Jeśli przyjmiemy, że log(8) = 3 (przy podstawie 2) oraz log(2) = 1, to mamy log(8/2) = 3 - 1 = 2. Takie podejście pozwala na szybkie i efektywne obliczenia logarytmów z ułamkami, niezależnie od ich złożoności.
Analizując wyniki tych obliczeń, widzimy, że logarytmy z ułamków mogą przyjmować wartości zarówno dodatnie, jak i ujemne, w zależności od wartości liczników i mianowników. Umożliwia to lepsze zrozumienie relacji między liczbami oraz ich zastosowanie w praktycznych problemach matematycznych. Obliczenia te pokazują, jak istotne jest zrozumienie podstawowych zasad logarytmów, aby móc skutecznie pracować z ułamkami.
Przykład 2: Obliczanie logarytmu z bardziej złożonym ułamkiem
W tym przykładzie zajmiemy się obliczeniem logarytmu z bardziej złożonego ułamka, na przykład 12/3. Aby obliczyć logarytm tego ułamka, korzystamy z reguły ilorazu: log(12/3) = log(12) - log(3). Przyjmując, że log(12) można obliczyć jako log(4) + log(3) (ponieważ 12 = 4 * 3), a log(4) = 2 (przy podstawie 2), możemy przekształcić nasz ułamek do postaci: log(12) = log(4) + log(3) = 2 + log(3).
Przyjmując, że log(3) wynosi około 1.585 (przy podstawie 2), obliczamy log(12) jako 2 + 1.585, co daje nam 3.585. Następnie, obliczamy log(3), co wynosi 1.585. Ostatecznie, log(12/3) = log(12) - log(3) = 3.585 - 1.585 = 2. Ta metoda pokazuje, jak można wykorzystać regułę ilorazu do obliczenia logarytmu z bardziej złożonymi ułamkami, co czyni ją bardzo przydatną w praktycznych zastosowaniach matematycznych.
Narzędzia i kalkulatory do obliczania logarytmów
W dzisiejszych czasach istnieje wiele narzędzi i kalkulatorów online, które mogą pomóc w obliczaniu logarytmów. Popularne kalkulatory, takie jak Symbolab, Desmos oraz Wolfram Alpha, umożliwiają szybkie obliczenia logarytmiczne, a także oferują dodatkowe funkcje, takie jak wykresy i szczegółowe wyjaśnienia. Te narzędzia są niezwykle pomocne dla studentów oraz osób pracujących z matematycznymi problemami, ponieważ pozwalają na szybkie i precyzyjne uzyskanie wyników.
Korzyści z korzystania z kalkulatorów online obejmują możliwość natychmiastowego uzyskania wyników oraz łatwość w obsłudze. Użytkownicy mogą wprowadzać różne wartości, a kalkulatory automatycznie obliczają logarytmy, co oszczędza czas i minimalizuje ryzyko błędów. Dodatkowo, wiele z tych narzędzi oferuje funkcje edukacyjne, które pomagają lepiej zrozumieć zasady logarytmów i ich zastosowania w praktyce.
Najlepsze kalkulatory online do logarytmów i ułamków
Wśród najlepszych kalkulatorów online do obliczania logarytmów znajdują się: Symbolab, Desmos, Wolfram Alpha oraz Calculator Soup. Symbolab oferuje funkcję krok po kroku, co jest pomocne dla osób uczących się. Desmos to świetne narzędzie do wizualizacji funkcji matematycznych, a Wolfram Alpha dostarcza szczegółowych informacji i przykładów. Calculator Soup jest prostym narzędziem, które szybko oblicza logarytmy i inne funkcje matematyczne.
Porównując te kalkulatory, warto zwrócić uwagę na ich funkcjonalność oraz łatwość obsługi. Na przykład, Symbolab daje możliwość uzyskania szczegółowych kroków obliczeń, co jest przydatne dla uczniów. Z kolei Desmos pozwala na wizualizację logarytmów na wykresach, co ułatwia zrozumienie ich zachowania. Wybór najlepszego narzędzia zależy od indywidualnych potrzeb użytkownika oraz poziomu zaawansowania w matematyce.
Jak korzystać z kalkulatora logarytmów krok po kroku
Aby skorzystać z kalkulatora logarytmów online, należy najpierw wybrać odpowiedni kalkulator, na przykład Symbolab. Następnie, w polu wejściowym wpisujemy ułamek lub liczbę, z której chcemy obliczyć logarytm. W przypadku wyboru logarytmu z ułamka, należy wpisać go w formacie, na przykład "log(12/3)". Po wprowadzeniu wartości, klikamy przycisk "Oblicz" lub "Wyślij", aby uzyskać wynik.
Wynik pojawi się na ekranie, a kalkulator może również pokazać szczegółowe kroki obliczeń, co pomoże zrozumieć proces. Warto zwrócić uwagę na dodatkowe funkcje kalkulatora, takie jak możliwość zmiany podstawy logarytmu lub wizualizacja wyników na wykresie. Dzięki temu, korzystanie z kalkulatorów online staje się nie tylko szybkie, ale także edukacyjne, co wspiera naukę matematyki.Jak logarytmy wpływają na algorytmy w nauce o danych
Logarytmy odgrywają kluczową rolę w nauce o danych, szczególnie w kontekście analizy dużych zbiorów danych oraz optymalizacji algorytmów. W praktycznych zastosowaniach, takich jak uczenie maszynowe, logarytmy są często wykorzystywane do przekształcania danych, co pozwala na lepsze modelowanie i interpretację wyników. Na przykład, algorytmy klasyfikacji mogą korzystać z logarytmicznych transformacji, aby poprawić wydajność i dokładność prognoz.
Dodatkowo, w kontekście big data, logarytmy pomagają w skalowaniu obliczeń. Dzięki zastosowaniu logarytmicznej skali, możliwe jest efektywne zarządzanie i przetwarzanie danych o dużej zmienności. W miarę jak technologia się rozwija, zrozumienie zastosowań logarytmów w algorytmach stanie się coraz bardziej istotne, a ich umiejętne wykorzystanie może przynieść znaczące korzyści w analizie danych i podejmowaniu decyzji opartych na danych.