Cotangens to jedna z podstawowych funkcji trygonometrycznych, która odgrywa kluczową rolę w matematyce, zwłaszcza w geometrii i analizie trigonometrycznej. Oznaczany symbolem ctg, cotangens jest definiowany jako stosunek długości przyprostokątnej leżącej przy kącie α do długości drugiej przyprostokątnej w trójkącie prostokątnym. Matematycznie można go wyrazić jako ctgα = cosα/sinα, co oznacza, że cotangens jest odwrotnością tangensa.
Zrozumienie cotangensa jest istotne nie tylko dla uczniów matematyki, ale również dla inżynierów, architektów i wszystkich, którzy pracują z geometrią. W tym artykule przyjrzymy się, czym jest cotangens, jak go obliczyć oraz jakie ma zastosowania w praktycznych problemach. Dowiemy się również, jak cotangens łączy się z innymi funkcjami trygonometrycznymi, co pozwoli nam lepiej zrozumieć jego znaczenie w szerszym kontekście matematycznym.
Kluczowe informacje:- Cotangens jest jedną z funkcji trygonometrycznych, definiowaną jako stosunek dwóch przyprostokątnych w trójkącie prostokątnym.
- Matematycznie cotangens można zapisać jako ctgα = cosα/sinα, co czyni go odwrotnością tangensa.
- Zrozumienie cotangensa jest kluczowe w matematyce, szczególnie w geometrii i trigonometrii.
- Cotangens znajduje zastosowanie w różnych dziedzinach, takich jak inżynieria czy architektura.
- Funkcja ta ma również istotne powiązania z innymi funkcjami trygonometrycznymi, takimi jak tangens i cosecant.
Cotangens: Definicja i podstawowe informacje o funkcji trygonometrycznej
Cotangens (oznaczany symbolem ctg) to jedna z podstawowych funkcji trygonometrycznych, która jest niezbędna w matematyce oraz w wielu dziedzinach nauki. Definiuje się go jako stosunek długości przyprostokątnej leżącej przy kącie α do długości drugiej przyprostokątnej w trójkącie prostokątnym. Dzięki tej definicji cotangens odgrywa kluczową rolę w rozwiązywaniu problemów związanych z kątami i długościami boków w trójkątach.
Matematycznie cotangens można wyrazić jako ctgα = cosα/sinα, co oznacza, że cotangens jest odwrotnością tangensa. Dzięki temu, gdy znamy wartości funkcji cosinus i sinus dla danego kąta, możemy łatwo obliczyć wartość cotangensa. Obliczanie cotangensa jest zatem proste i intuicyjne, co czyni go użytecznym narzędziem w matematyce.
Czym jest cotangens i jak go obliczyć?
Cotangens to funkcja, która znajduje zastosowanie w różnych obszarach matematyki, takich jak geometria i analiza trigonometryczna. Jest to funkcja, która pomaga w zrozumieniu relacji między kątami a bokami trójkątów prostokątnych. Cotangens jest szczególnie przydatny w kontekście kątów ostrych, gdzie jego wartość może być łatwo obliczona na podstawie długości boków trójkąta.
Aby obliczyć cotangens, wystarczy znać wartości funkcji cosinus i sinus dla danego kąta. Wzór na cotangens wygląda następująco: ctgα = cosα/sinα. Na przykład, dla kąta 45° mamy: cos(45°) = √2/2 oraz sin(45°) = √2/2. Wówczas cotangens 45° obliczamy jako ctg(45°) = (√2/2) / (√2/2) = 1. Obliczenia te pokazują, jak łatwo można wykorzystać cotangens w praktyce.
Dlaczego cotangens jest ważny w matematyce?
Cotangens jest istotną funkcją w matematyce, szczególnie w kontekście trigonometrii i geometrii. Jego znaczenie wynika z tego, że pozwala na zrozumienie relacji między kątami a długościami boków w trójkątach prostokątnych. Cotangens jest również używany do analizy różnych zjawisk w naukach ścisłych, takich jak fizyka czy inżynieria, co czyni go uniwersalnym narzędziem w wielu dziedzinach.
Dzięki swojej prostocie i łatwości obliczeń, cotangens znajduje zastosowanie w różnych problemach matematycznych. Umożliwia on także przekształcanie i rozwiązywanie równań trygonometrycznych. W związku z tym, zrozumienie tej funkcji jest kluczowe dla uczniów oraz profesjonalistów, którzy pracują z geometrią i analizą matematyczną.
Jak cotangens wpływa na obliczenia w trójkątach prostokątnych?
Cotangens odgrywa kluczową rolę w obliczeniach związanych z trójkątami prostokątnymi. Umożliwia łatwe wyznaczanie długości boków oraz kątów, co jest istotne w wielu zastosowaniach, od geometrii po inżynierię. W kontekście trójkątów prostokątnych, cotangens jest definiowany jako stosunek długości przyprostokątnej leżącej przy kącie α do długości przeciwległej przyprostokątnej. Dzięki temu, gdy znamy długości boków trójkąta, możemy szybko obliczyć wartość cotangensa i wykorzystać ją do dalszych obliczeń.
Na przykład, w trójkącie prostokątnym o kącie α, jeśli długość przyprostokątnej przyległej wynosi 4 jednostki, a długość przeciwległej wynosi 3 jednostki, cotangens kąta α można obliczyć jako ctgα = przyprostokątna przyległa / przyprostokątna przeciwległa = 4 / 3. Wartość ta jest równa około 1,33. Tego rodzaju obliczenia są niezwykle przydatne w praktyce, zwłaszcza przy projektowaniu konstrukcji czy rozwiązywaniu problemów inżynieryjnych.
Przykłady zastosowania cotangens w praktycznych problemach
Cotangens znajduje szerokie zastosowanie w rzeczywistych problemach, gdzie konieczne jest wyznaczenie kątów lub długości boków w trójkątach prostokątnych. Na przykład, w architekturze, inżynierowie często muszą obliczać kąty nachylenia dachów. Znając długości boków, mogą użyć cotangensa do określenia odpowiedniego kąta, co pozwala na precyzyjne zaprojektowanie konstrukcji.
Kolejnym przykładem może być zastosowanie cotangensa w nawigacji. Marynarze i piloci często muszą obliczać kursy i odległości, aby dotrzeć do celu. W takich sytuacjach, znajomość cotangensa pozwala na szybkie obliczenia, które są kluczowe w sytuacjach wymagających dużej precyzji. Na przykład, jeśli statek znajduje się w odległości 10 mil od portu i musi zmienić kurs o 30°, może użyć cotangensa do obliczenia nowej odległości do portu oraz czasu potrzebnego na dotarcie do celu.
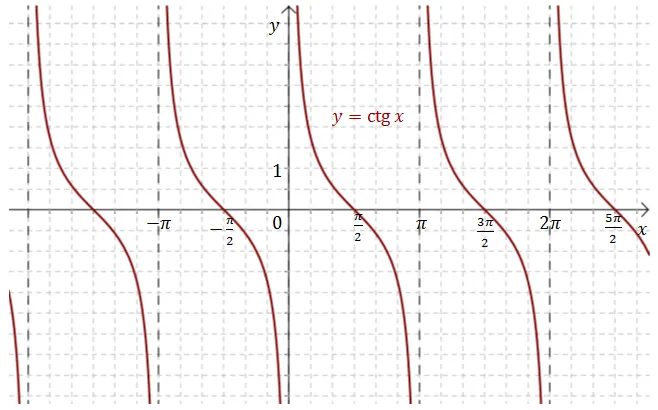
Relacje cotangens z innymi funkcjami trygonometrycznymi
Cotangens ma istotne relacje z innymi funkcjami trygonometrycznymi, takimi jak tangens i cosecant. Zrozumienie tych powiązań jest kluczowe dla właściwego stosowania cotangensa w różnych kontekstach matematycznych. W szczególności, cotangens można wyrazić jako odwrotność tangensa, co pozwala na łatwe przekształcanie wyrażeń trygonometrycznych oraz rozwiązywanie równań. Ponadto, cotangens jest również związany z funkcją cosecant, co otwiera dodatkowe możliwości w analizie funkcji trygonometrycznych.
Relacja między cotangensem a tangensem jest prosta: ctgα = 1/tgα. Oznacza to, że jeśli znamy wartość tangensa, możemy łatwo obliczyć cotangens i odwrotnie. Na przykład, jeśli tangens kąta α wynosi 2, to cotangens tego kąta wynosi 1/2. Ta odwrotność jest niezwykle przydatna w obliczeniach, ponieważ pozwala na szybką konwersję między tymi dwiema funkcjami, co jest szczególnie użyteczne w bardziej złożonych zadaniach matematycznych.
W przypadku funkcji cosecant, cotangens jest związany z nią poprzez tożsamość: ctgα = cosα/sinα, co wskazuje na relację między tymi funkcjami. Cosecant jest odwrotnością funkcji sinus, a zatem można go wykorzystać do obliczeń związanych z cotangensem. Przykładowo, jeśli znamy wartość sin(α), możemy obliczyć cosecant jako 1/sin(α), a następnie użyć tej wartości do dalszych obliczeń z cotangensem, co czyni te funkcje współzależnymi i bardzo przydatnymi w analizach trygonometrycznych.
Jak cotangens odnosi się do tangensa i cosecanta?
Cotangens ma bezpośrednią relację z tangensem i cosecantem, co czyni go istotnym elementem w trygonometrii. Z definicji, cotangens jest odwrotnością tangensa, co oznacza, że jeśli znamy wartość tangensa, możemy szybko znaleźć cotangens, stosując prostą formułę. Na przykład, dla kąta α, jeżeli tangens wynosi 0.5, cotangens będzie równy 2. Ta właściwość ułatwia obliczenia i pozwala na szybsze rozwiązywanie problemów matematycznych.
Relacja cotangensa z cosecantem jest równie ważna. Możemy zapisać ją jako ctgα = 1/tgα = cosα/sinα. Oznacza to, że cotangens można obliczyć, znając wartości cosinusa i sinusa. W praktyce, jeśli mamy wartość cosecant (np. 1.5), możemy łatwo znaleźć cotangens, przekształcając równanie. Ta współzależność między funkcjami trygonometrycznymi jest kluczowa w wielu zastosowaniach matematycznych, ponieważ pozwala na elastyczne podejście do rozwiązywania równań i problemów geometrycznych.
Zrozumienie wzorów i tożsamości trygonometrycznych z cotangensem
Tożsamości trygonometryczne są kluczowe dla zrozumienia, jak cotangens funkcjonuje w kontekście innych funkcji trygonometrycznych. Cotangens, oznaczany symbolem ctg, ma swoje unikalne tożsamości, które można wykorzystać do przekształcania równań i rozwiązywania problemów matematycznych. Na przykład, jedna z podstawowych tożsamości to ctgα = 1/tgα, co oznacza, że cotangens jest odwrotnością tangensa. Tego rodzaju tożsamości pozwalają na łatwe przekształcanie funkcji, co jest niezwykle przydatne w matematyce.
Inna ważna tożsamość to ctgα = cosα/sinα. Umożliwia ona obliczenie cotangensa, znając wartości funkcji cosinus i sinus. Przykładowo, jeśli cos(30°) = √3/2 i sin(30°) = 1/2, to cotangens kąta 30° można obliczyć jako ctg(30°) = (√3/2) / (1/2) = √3. Takie tożsamości są nie tylko teoretyczne, ale mają również praktyczne zastosowanie w rozwiązywaniu równań trygonometrycznych oraz w analizie geometrycznej.
- ctgα = 1/tgα - Cotangens jako odwrotność tangensa.
- ctgα = cosα/sinα - Cotangens w zależności od cosinusa i sinusa.
- ctg(90° - α) = tgα - Związek cotangensa z tangensem kąta dopełniającego.
Czytaj więcej: Najlepsze zabawy z piłką w kole - 7 sprawdzonych gier dla dzieci i młodzieży
Praktyczne zastosowania cotangensa w informatyce i grafice 3D
Cotangens znajduje również zastosowanie w informatyce oraz grafice komputerowej, szczególnie w kontekście modelowania 3D i obliczeń związanych z oświetleniem. W programowaniu gier i aplikacji graficznych, cotangens jest wykorzystywany do obliczania kątów i proporcji w przestrzeni trójwymiarowej. Dzięki znajomości cotangensa, programiści mogą precyzyjnie określać, jak obiekty wirtualne powinny się poruszać i jak powinny być oświetlane w zależności od kątów widzenia, co znacząco wpływa na realizm i immersję w grach.
Przykładowo, w silnikach graficznych, cotangens może być użyty do obliczania kątów padania światła na powierzchnie obiektów, co pozwala na uzyskanie efektów cieniowania i refleksów. Używając cotangensa do określenia kątów w przestrzeni, programiści mogą również zoptymalizować algorytmy kolizji, co jest kluczowe dla płynności rozgrywki. W przyszłości, z rozwojem technologii VR i AR, rola cotangensa w tych dziedzinach prawdopodobnie wzrośnie, co otworzy nowe możliwości dla twórców i inżynierów zajmujących się grafiką komputerową.
