Obliczanie wysokości w trójkącie prostokątnym jest istotnym zagadnieniem w geometrii, które można rozwiązać na różne sposoby, w zależności od dostępnych danych. Wysokość trójkąta prostokątnego można obliczyć, znając długości przyprostokątnych, przeciwprostokątnej, pole trójkąta, a także kąty. W artykule przedstawimy różne wzory i metody, które pomogą w dokładnym obliczeniu wysokości, unikając przy tym typowych błędów i wpadek.
Każda z metod obliczania wysokości jest dostosowana do różnych sytuacji, co sprawia, że zrozumienie ich zastosowania jest kluczowe dla uzyskania poprawnych wyników. Dzięki temu artykułowi nauczysz się, jak wykorzystać konkretne wzory w praktyce oraz jakie pułapki mogą cię spotkać podczas obliczeń.
Kluczowe informacje:- Wysokość w trójkącie prostokątnym można obliczyć na kilka sposobów, w zależności od znanych danych.
- Znając długości przyprostokątnych, można użyć wzoru: h = (a * b) / c.
- Jeśli znasz pole trójkąta i długość przeciwprostokątnej, zastosuj wzór: h = (2 * P) / c.
- Wysokość można również obliczyć, znając długość przeciwprostokątnej i jeden z kątów, używając wzoru: h = c * sin(α).
- Ważne jest unikanie typowych błędów, takich jak błędne stosowanie wzorów czy niepoprawne wprowadzanie danych.
Jak obliczyć wysokość w trójkącie prostokątnym w prosty sposób
Obliczanie wysokości w trójkącie prostokątnym może wydawać się trudne, ale istnieje kilka prostych metod, które pozwalają na jej dokładne określenie. Wysokość trójkąta prostokątnego jest kluczowym elementem w wielu obliczeniach geometrycznych. W zależności od dostępnych danych, można używać różnych wzorów, aby uzyskać prawidłowy wynik. Najczęściej stosowane metody obliczania wysokości opierają się na długościach przyprostokątnych oraz przeciwprostokątnej. Zrozumienie tych wzorów i ich zastosowania jest niezbędne, aby uniknąć błędów w obliczeniach. Poniżej przedstawiamy kilka podstawowych wzorów, które pomogą w ustaleniu wysokości w trójkącie prostokątnym.Wzór na wysokość z długości przyprostokątnych i przeciwprostokątnej
Jednym z najprostszych sposobów obliczania wysokości w trójkącie prostokątnym jest wykorzystanie długości przyprostokątnych oraz przeciwprostokątnej. Wzór, który można zastosować, to h = (a * b) / c, gdzie a i b to długości przyprostokątnych, a c to długość przeciwprostokątnej. Dzięki temu wzorowi można łatwo obliczyć wysokość, mając dane o długościach boków.Na przykład, jeśli długości przyprostokątnych wynoszą 3 cm i 4 cm, a długość przeciwprostokątnej to 5 cm, wysokość obliczamy w następujący sposób: h = (3 * 4) / 5 = 12 / 5 = 2.4 cm. Takie obliczenie pozwala na szybkie i skuteczne określenie wysokości w trójkącie prostokątnym.
Jak obliczyć wysokość znając pole trójkąta i przeciwprostokątną
Obliczanie wysokości trójkąta prostokątnego, gdy znane są pole trójkąta oraz długość przeciwprostokątnej, można wykonać przy użyciu wzoru: h = (2 * P) / c. W tym wzorze P oznacza pole trójkąta, a c to długość przeciwprostokątnej. Dzięki temu wzorowi można łatwo wyznaczyć wysokość, mając jedynie dane o polu i długości najdłuższego boku.
Na przykład, jeśli pole trójkąta wynosi 12 cm², a długość przeciwprostokątnej to 5 cm, obliczamy wysokość w następujący sposób: h = (2 * 12) / 5 = 24 / 5 = 4.8 cm. Taki sposób obliczeń jest bardzo przydatny w sytuacjach, gdy nie znamy długości przyprostokątnych, ale mamy dostęp do informacji o polu trójkąta.
Wysokość w trójkącie prostokątnym z kątami i bokami
Wysokość trójkąta prostokątnego można również obliczyć, wykorzystując kąty oraz długość przeciwprostokątnej. Ta metoda jest szczególnie przydatna, gdy znamy jeden z kątów ostrych. Wzór, który można zastosować w tym przypadku, to h = c * sin(α), gdzie α to miara kąta. Dzięki temu wzorowi możemy uzyskać wysokość, znając tylko długość przeciwprostokątnej oraz kąt.
Na przykład, jeśli długość przeciwprostokątnej wynosi 10 cm, a kąt ostry ma miarę 30 stopni, wysokość obliczamy w następujący sposób: h = 10 * sin(30°) = 10 * 0.5 = 5 cm. Tego rodzaju obliczenia są niezwykle przydatne w praktyce, zwłaszcza w architekturze czy inżynierii, gdzie często musimy pracować z kątami i długościami boków.
Obliczanie wysokości przy znanej długości przeciwprostokątnej
Obliczanie wysokości trójkąta prostokątnego, gdy znana jest długość przeciwprostokątnej, można wykonać przy użyciu wzoru: h = \sqrt{c^2 - a^2}, gdzie c to długość przeciwprostokątnej, a a to jedna z przyprostokątnych. Wzór ten pozwala na wyznaczenie wysokości, gdy mamy dane o długości przeciwprostokątnej oraz jednej z przyprostokątnych. Jest to przydatne w sytuacjach, gdy nie możemy bezpośrednio zmierzyć wysokości, ale znamy długości boków.
Na przykład, jeśli długość przeciwprostokątnej wynosi 10 cm, a jedna z przyprostokątnych ma długość 6 cm, wysokość obliczamy następująco: h = \sqrt{10^2 - 6^2} = \sqrt{100 - 36} = \sqrt{64} = 8 cm. Takie obliczenia są niezwykle pomocne w geometrii, umożliwiając szybkie określenie wysokości trójkąta prostokątnego.
Wysokość trójkąta prostokątnego z kątem ostrym
Obliczanie wysokości trójkąta prostokątnego z wykorzystaniem kąta ostrego to kolejna efektywna metoda. Wzór, który można zastosować, to h = a * \tan(α), gdzie a to długość jednej z przyprostokątnych, a α to miara kąta ostrego. Dzięki temu wzorowi możemy obliczyć wysokość, mając dane o długości przyprostokątnej oraz kącie.
Na przykład, jeśli długość przyprostokątnej wynosi 4 cm, a kąt ostry ma miarę 45 stopni, obliczamy wysokość w następujący sposób: h = 4 * \tan(45°) = 4 * 1 = 4 cm. Tego rodzaju obliczenia są szczególnie przydatne w praktyce, na przykład w budownictwie, gdzie często wykorzystuje się kąt do określenia wysokości różnych struktur.
Czytaj więcej: Jak skutecznie napisać podanie o przeniesienie do innej szkoły: 8 argumentów
Praktyczne przykłady obliczania wysokości w trójkącie prostokątnym
Obliczanie wysokości w trójkącie prostokątnym można przeprowadzić na wiele sposobów, w zależności od dostępnych danych. W tej sekcji przedstawimy kilka praktycznych przykładów, które ilustrują różne metody obliczania wysokości. Dzięki tym przykładom łatwiej będzie zrozumieć, jak wykorzystać odpowiednie wzory w praktyce.
Na przykład, jeśli mamy trójkąt prostokątny, w którym długości przyprostokątnych wynoszą 6 cm i 8 cm, a długość przeciwprostokątnej to 10 cm, możemy obliczyć wysokość, korzystając z wzoru h = (a * b) / c. W naszym przypadku: h = (6 * 8) / 10 = 48 / 10 = 4.8 cm. To pokazuje, jak prosto można obliczyć wysokość, znając długości boków trójkąta.
| Metoda | Dane wejściowe | Wysokość (cm) |
|---|---|---|
| Przyprostokątne i przeciwprostokątna | a = 6 cm, b = 8 cm, c = 10 cm | 4.8 |
| Pole i przeciwprostokątna | P = 24 cm², c = 10 cm | 4.8 |
Krok po kroku: obliczanie wysokości na konkretnych przykładach
Aby obliczyć wysokość trójkąta prostokątnego krok po kroku, rozważmy przykład, w którym pole trójkąta wynosi 24 cm², a długość przeciwprostokątnej to 10 cm. Najpierw zastosujemy wzór h = (2 * P) / c. W naszym przypadku: h = (2 * 24) / 10 = 48 / 10 = 4.8 cm. W ten sposób, krok po kroku, uzyskujemy wysokość trójkąta, korzystając z dostępnych danych o polu i przeciwprostokątnej.
Wizualne przedstawienie obliczeń wysokości w trójkącie
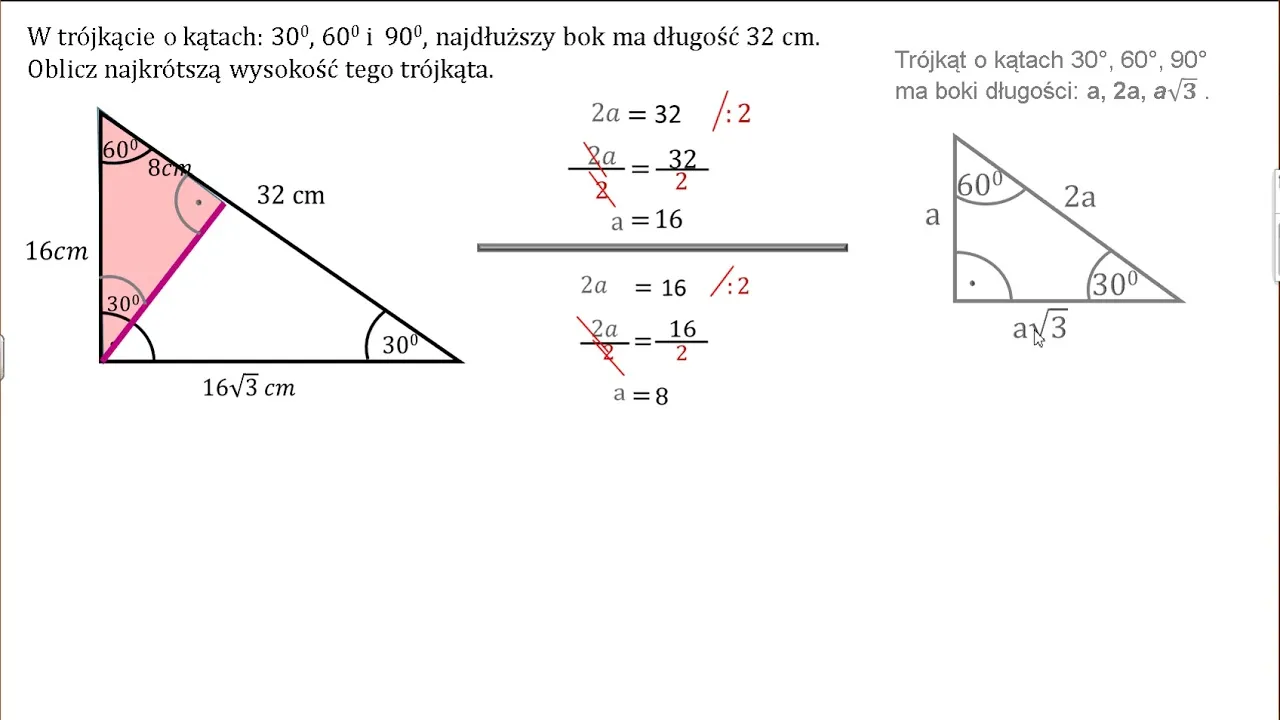
Wizualizacja obliczeń wysokości w trójkącie prostokątnym jest niezwykle ważna, ponieważ pomaga zrozumieć, jak różne elementy trójkąta są ze sobą powiązane. Diagramy i rysunki mogą znacząco ułatwić proces nauki, pokazując, jak obliczenia są realizowane w praktyce. Dzięki wizualnym przedstawieniom można lepiej uchwycić koncepcje, takie jak relacje między bokami trójkąta oraz wysokością.
Na przykład, rysując trójkąt prostokątny z oznaczonymi długościami boków oraz wysokością, uczniowie mogą łatwiej zrozumieć, jak stosować odpowiednie wzory. Tego typu wizualizacje są szczególnie przydatne w edukacji, gdzie graficzne przedstawienie danych wspiera proces przyswajania wiedzy. Warto zainwestować czas w tworzenie diagramów, które pomogą w nauce obliczeń wysokości w trójkącie prostokątnym.
Najczęstsze błędy w obliczaniu wysokości w trójkącie prostokątnym
Podczas obliczania wysokości w trójkącie prostokątnym można popełnić wiele typowych błędów. Jednym z najczęstszych jest niewłaściwe stosowanie wzorów, co prowadzi do błędnych wyników. Na przykład, mylenie długości boków lub nieprawidłowe wprowadzenie danych do wzoru może skutkować znacznymi różnicami w końcowych obliczeniach.
Kolejnym powszechnym błędem jest nieprawidłowe zrozumienie relacji między bokami trójkąta. Uczniowie często zapominają, że wysokość trójkąta prostokątnego jest zawsze prostopadła do podstawy, co może prowadzić do błędnych obliczeń. Ważne jest, aby przed przystąpieniem do obliczeń dokładnie zrozumieć, jakie informacje są potrzebne i jak je poprawnie zastosować.
Jak wykorzystać obliczenia wysokości w trójkącie w praktyce
Obliczenia wysokości w trójkącie prostokątnym mają szerokie zastosowanie w różnych dziedzinach, takich jak architektura, inżynieria czy geodezja. Znajomość metod obliczania wysokości pozwala na dokładne projektowanie struktur, które muszą spełniać określone normy bezpieczeństwa i estetyki. Na przykład, w architekturze wysokość trójkąta prostokątnego może być kluczowa przy projektowaniu dachów, gdzie odpowiednie kąty i wysokości wpływają na efektywność odprowadzania wody deszczowej oraz stabilność konstrukcji.
Dodatkowo, w kontekście nowoczesnych technologii, takich jak modelowanie informacji o budynkach (BIM), obliczenia wysokości mogą być automatyzowane i integrowane z oprogramowaniem projektowym. Umożliwia to inżynierom i architektom szybkie analizowanie różnych wariantów projektowych oraz optymalizację kosztów i materiałów. Warto zatem zainwestować w naukę zaawansowanych technik obliczeniowych, które mogą znacznie ułatwić pracę w branży budowlanej i projektowej.

