Sinus to jedno z podstawowych pojęć w trygonometrii, które odgrywa kluczową rolę w zrozumieniu relacji między kątami a bokami trójkątów prostokątnych. W prostych słowach, sinus kąta ostrego opisuje stosunek długości boku naprzeciw kąta do długości przeciwprostokątnej. Dzięki tej funkcji możemy obliczać różne wartości, które są niezwykle przydatne w wielu dziedzinach, takich jak fizyka, inżynieria czy nawigacja.
W artykule przyjrzymy się, jak zdefiniować sinus, jakie są jego właściwości oraz jak można go zastosować w praktyce. Zrozumienie tej funkcji nie tylko ułatwia naukę matematyki, ale także pozwala na zastosowanie jej w realnych sytuacjach. Odkryjemy również, jak wizualizować sinus za pomocą diagramów, co pomoże w lepszym zrozumieniu tego zagadnienia. Kluczowe informacje:- Sinus kąta ostrego to stosunek długości przyprostokątnej do długości przeciwprostokątnej w trójkącie prostokątnym.
- Wzór na sinus jest kluczowy w obliczeniach trygonometrycznych: sin α = długość przeciwległej / długość przeciwprostokątnej.
- Sinus ma zastosowanie w różnych dziedzinach, takich jak fizyka, inżynieria i nawigacja.
- Właściwości funkcji sinus obejmują jej okresowość oraz amplitudę, co jest istotne dla analizy matematycznej.
- Wizualizacja sinusa za pomocą diagramów ułatwia zrozumienie jego zastosowania w praktyce.
Definicja sinusa i jego rola w trygonometrii
Sinus jest kluczowym pojęciem w trygonometrii, które odnosi się do relacji między kątami a bokami trójkątów prostokątnych. W najprostszej definicji, sinus kąta ostrego to stosunek długości boku naprzeciw kąta do długości przeciwprostokątnej. Dzięki tej funkcji możemy zrozumieć, jak różne kąty wpływają na długości boków trójkąta. Sinus jest nie tylko istotny w matematyce, ale również w wielu praktycznych zastosowaniach, takich jak inżynieria czy nawigacja.
W kontekście trygonometrii, sinus odgrywa fundamentalną rolę w obliczeniach związanych z kątami i bokami trójkątów prostokątnych. Zrozumienie tej funkcji jest kluczowe dla dalszego poznawania bardziej zaawansowanych zagadnień matematycznych. W kolejnych częściach artykułu przyjrzymy się, jak dokładnie zdefiniować sinus w kontekście trójkątów prostokątnych oraz dlaczego jest on tak ważny w nauce matematyki.
Jak zdefiniować sinus w kontekście trójkątów prostokątnych?
Sinus kąta ostrego w trójkącie prostokątnym definiuje się jako stosunek długości przyprostokątnej, która leży naprzeciw kąta, do długości przeciwprostokątnej. Można to zapisać matematycznie jako sin α = (długość przyprostokątnej naprzeciw kąta α) / (długość przeciwprostokątnej). Na przykład, jeśli w trójkącie prostokątnym długość boku naprzeciw kąta wynosi 3 jednostki, a długość przeciwprostokątnej to 5 jednostek, to sinus tego kąta wynosi 0,6. Taka definicja sinusa jest fundamentalna dla dalszych badań w trygonometrii i pomaga w zrozumieniu, jak kąty wpływają na geometrę trójkątów.Dlaczego sinus jest kluczowym pojęciem w matematyce?
Sinus jest kluczowym pojęciem w matematyce, szczególnie w trygonometrii, ponieważ stanowi fundament dla wielu bardziej zaawansowanych zagadnień. Zrozumienie sinusa pozwala na lepsze pojęcie relacji między kątami a bokami trójkątów prostokątnych, co jest niezbędne w różnych dziedzinach nauki. Dzięki sinusowi uczniowie mogą rozwijać umiejętności analityczne, które są przydatne nie tylko w matematyce, ale także w fizyce i inżynierii. Właściwe zrozumienie tej funkcji otwiera drzwi do bardziej skomplikowanych koncepcji, takich jak trygonometria sferyczna czy analiza harmoniczna.
Sinus jest również istotny w kontekście rozwoju umiejętności rozwiązywania problemów. Uczy uczniów, jak stosować teoretyczne pojęcia w praktycznych sytuacjach, co zwiększa ich zdolności krytycznego myślenia. Warto zauważyć, że sinus jest także używany w różnych zastosowaniach praktycznych, które będziemy omawiać w kolejnych sekcjach. Właściwe zrozumienie sinusa jest zatem nie tylko kluczowe dla nauki matematyki, ale również dla zastosowań w życiu codziennym.
Matematyczna formuła sinusa i jej zastosowanie
Matematyczna formuła sinusa jest podstawowym narzędziem w trygonometrii, umożliwiającym obliczanie wartości sinus dla różnych kątów. Sinus kąta α można zapisać jako sin α = (długość przyprostokątnej naprzeciw kąta α) / (długość przeciwprostokątnej). Ta prosta relacja jest niezwykle użyteczna w obliczeniach związanych z trójkątami prostokątnymi. Dzięki tej formule możemy obliczać długości boków trójkątów, co jest niezbędne w wielu dziedzinach, takich jak inżynieria, architektura czy nawigacja.
W praktyce, zastosowanie funkcji sinus może obejmować różnorodne scenariusze. Na przykład, w inżynierii, sinus jest używany do obliczania kątów w konstrukcjach, a w fizyce do analizy fal i drgań. W kolejnych częściach artykułu przyjrzymy się konkretnym zastosowaniom sinusa w różnych dziedzinach, co pomoże lepiej zrozumieć jego znaczenie w rzeczywistych sytuacjach. Sinus jest zatem nie tylko teoretycznym pojęciem, ale również narzędziem o szerokim zakresie zastosowań.
Jak obliczyć wartość sinusa dla kąta ostrego?
Aby obliczyć wartość sinusa dla kąta ostrego, można skorzystać z prostego wzoru, który opiera się na stosunku długości boków w trójkącie prostokątnym. Sinus kąta α można zapisać jako sin α = (długość przyprostokątnej naprzeciw kąta α) / (długość przeciwprostokątnej). Przykładowo, jeśli w trójkącie prostokątnym długość boku naprzeciw kąta wynosi 4 jednostki, a długość przeciwprostokątnej to 5 jednostek, to wartość sinusa tego kąta wynosi 0,8. Obliczenia te są niezwykle przydatne w różnych dziedzinach, takich jak inżynieria czy architektura.
Kroki do obliczenia sinusa są następujące: najpierw należy zmierzyć długość przyprostokątnej naprzeciw kąta, następnie zmierzyć długość przeciwprostokątnej, a na końcu podzielić długość przyprostokątnej przez długość przeciwprostokątnej. Dzięki tym prostym krokom można szybko i łatwo obliczyć sinus dla dowolnego kąta ostrego. Pamiętaj, że wartości sinusa dla kątów można również znaleźć w tabelach trygonometrycznych lub przy użyciu kalkulatorów naukowych.
Jakie są właściwości funkcji sinus w trygonometrii?
Funkcja sinus ma kilka kluczowych właściwości, które są istotne w trygonometrii. Po pierwsze, sinus jest funkcją okresową, co oznacza, że powtarza swoje wartości co 360 stopni (lub 2π radiany). Oznacza to, że dla każdego kąta α, sin(α) = sin(α + 360°n), gdzie n jest liczbą całkowitą. Kolejną ważną właściwością jest to, że sinus kąta w przedziale od 0° do 90° jest zawsze dodatni, a jego wartość osiąga maksimum 1 dla kąta 90°.
Sinus jest również funkcją nieparzystą, co oznacza, że sin(-α) = -sin(α). Ta cecha jest przydatna przy rozwiązywaniu równań trygonometrycznych. Dodatkowo, sinus wykazuje różne wartości dla kątów w różnych ćwiartkach układu współrzędnych, co ma istotne znaczenie w analizie funkcji trygonometrycznych. Zrozumienie tych właściwości jest kluczowe dla dalszego zgłębiania tematu trygonometrii i jej zastosowań.
Czytaj więcej: Co zrobić gdy dziecko jest wyśmiewane w szkole: 8 skutecznych metod
Praktyczne zastosowania sinusa w różnych dziedzinach
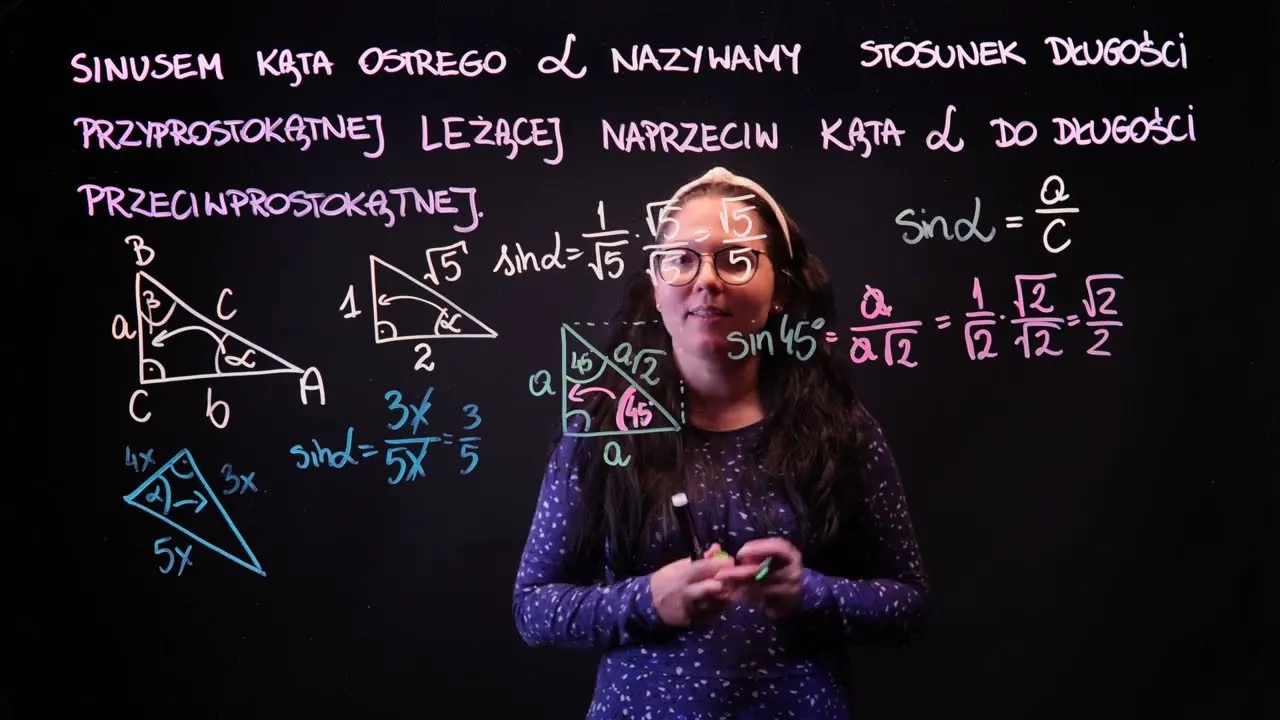
Sinus znajduje szerokie zastosowanie w różnych dziedzinach, takich jak fizyka, inżynieria czy nawigacja. W inżynierii, sinus jest kluczowy przy projektowaniu konstrukcji, gdzie obliczenia kątów i długości są niezbędne do zapewnienia stabilności budowli. Na przykład, inżynierowie korzystają z funkcji sinus, aby określić odpowiednie kąty nachylenia dachów, co wpływa na ich wydajność i odporność na warunki atmosferyczne. W fizyce, sinus jest używany do analizy fal, takich jak fale dźwiękowe czy elektromagnetyczne, co pozwala na zrozumienie ich właściwości i zachowania.
W nawigacji, funkcja sinus odgrywa istotną rolę w obliczeniach związanych z pozycjonowaniem i trasowaniem. Dzięki sinusowi, nawigatorzy mogą określić kąt, pod jakim należy skręcić, aby osiągnąć cel. Warto również zauważyć, że sinus jest używany w technologii GPS, co czyni go niezbędnym narzędziem w nowoczesnym transporcie. Poniżej przedstawiamy tabelę z przykładami zastosowania funkcji sinus w różnych dziedzinach, co pomoże lepiej zrozumieć jej znaczenie w praktyce.
| Domena | Zastosowanie |
|---|---|
| Inżynieria | Obliczanie kątów nachylenia dachów i konstrukcji |
| Fizyka | Analiza fal dźwiękowych i elektromagnetycznych |
| Nawigacja | Obliczenia kątów skrętu w trasowaniu |
Jak sinus jest wykorzystywany w fizyce i inżynierii?
W fizyce, sinus jest kluczowy w analizie zjawisk falowych, takich jak fale dźwiękowe i świetlne. Na przykład, w mechanice fal, sinus opisuje zmiany amplitudy fali w czasie, co jest istotne dla zrozumienia zjawisk akustycznych. W inżynierii, sinus jest wykorzystywany w obliczeniach dotyczących sygnałów, na przykład w technologii komunikacyjnej, gdzie analiza sygnałów sinusoidalnych jest niezbędna do przesyłania danych. Dzięki funkcji sinus, inżynierowie mogą projektować bardziej efektywne systemy, które są w stanie transmitować informacje na dużą odległość.
Jakie są przykłady zastosowań sinusa w codziennym życiu?
Sinus znajduje wiele praktycznych zastosowań w codziennym życiu, które są często niedoceniane. Na przykład, w architekturze, architekci używają funkcji sinus do obliczania kątów i długości w projektach budowlanych, co pozwala na tworzenie stabilnych i estetycznych konstrukcji. W nawigacji, sinus jest wykorzystywany do określenia kierunków i tras, co jest kluczowe dla żeglarzy i pilotów. Dzięki funkcji sinus, możliwe jest dokładne obliczenie odległości i kątów, co zwiększa bezpieczeństwo podróży.
Innym przykładem zastosowania sinusa w codziennym życiu jest w technologii GPS, gdzie obliczenia oparte na funkcji sinus są używane do precyzyjnego określenia pozycji. Sinus jest także istotny w muzyce, gdzie opisuje fale dźwiękowe, co pozwala na tworzenie harmonijnych dźwięków. Te przykłady pokazują, jak funkcja sinus jest integralną częścią wielu aspektów naszego codziennego życia, wpływając na różnorodne dziedziny i ułatwiając wiele procesów.
Wizualizacja sinusa: diagramy i ilustracje krok po kroku
Wizualizacja sinusa jest kluczowa dla lepszego zrozumienia tej funkcji. Diagramy i ilustracje pomagają zobrazować, jak sinus wpływa na kształt trójkątów prostokątnych oraz jak zmienia się w zależności od kątów. Wizualne przedstawienie sinusa umożliwia łatwiejsze przyswajanie wiedzy i ułatwia naukę. Warto korzystać z różnych narzędzi, takich jak programy graficzne czy aplikacje edukacyjne, aby tworzyć dokładne i czytelne diagramy.
Aby stworzyć skuteczne diagramy, należy skupić się na klarowności i precyzji. Należy zacząć od narysowania trójkąta prostokątnego, oznaczenia kątów oraz długości boków. Następnie, warto dodać opisy, które wyjaśnią, co przedstawia każdy element diagramu. Użycie kolorów i różnych stylów linii może również pomóc w lepszym zrozumieniu zagadnienia. Poniżej przedstawiamy listę narzędzi, które mogą być użyte do wizualizacji sinusa:
- GeoGebra – interaktywne oprogramowanie do nauki matematyki
- Desmos – kalkulator graficzny online, który umożliwia rysowanie funkcji
- Microsoft PowerPoint – program do tworzenia prezentacji, który umożliwia rysowanie diagramów
Nowe technologie w zastosowaniach funkcji sinus w inżynierii
W miarę jak technologia się rozwija, zastosowania funkcji sinus w inżynierii stają się coraz bardziej zaawansowane i złożone. Na przykład, w projektowaniu struktur z wykorzystaniem modelowania informacji o budynkach (BIM), inżynierowie mogą używać funkcji sinus do symulacji zachowania konstrukcji pod wpływem różnych sił, takich jak wiatry czy obciążenia dynamiczne. Dzięki temu możliwe jest przewidywanie, jak różne kształty i kąty wpływają na stabilność budowli, co prowadzi do bardziej efektywnych i bezpiecznych projektów.
Dodatkowo, w dziedzinie robotyki i automatyki, funkcje sinusowe są wykorzystywane w algorytmach sterujących do precyzyjnego ruchu i nawigacji robotów. Wykorzystanie sinusa w analizie danych z czujników pozwala na lepsze zrozumienie i interpretację otoczenia, co jest kluczowe w tworzeniu autonomicznych systemów. Przyszłość zastosowań funkcji sinus w tych dziedzinach wydaje się obiecująca, a ich integracja z nowoczesnymi technologiami może przynieść znaczące innowacje w inżynierii i technologii.