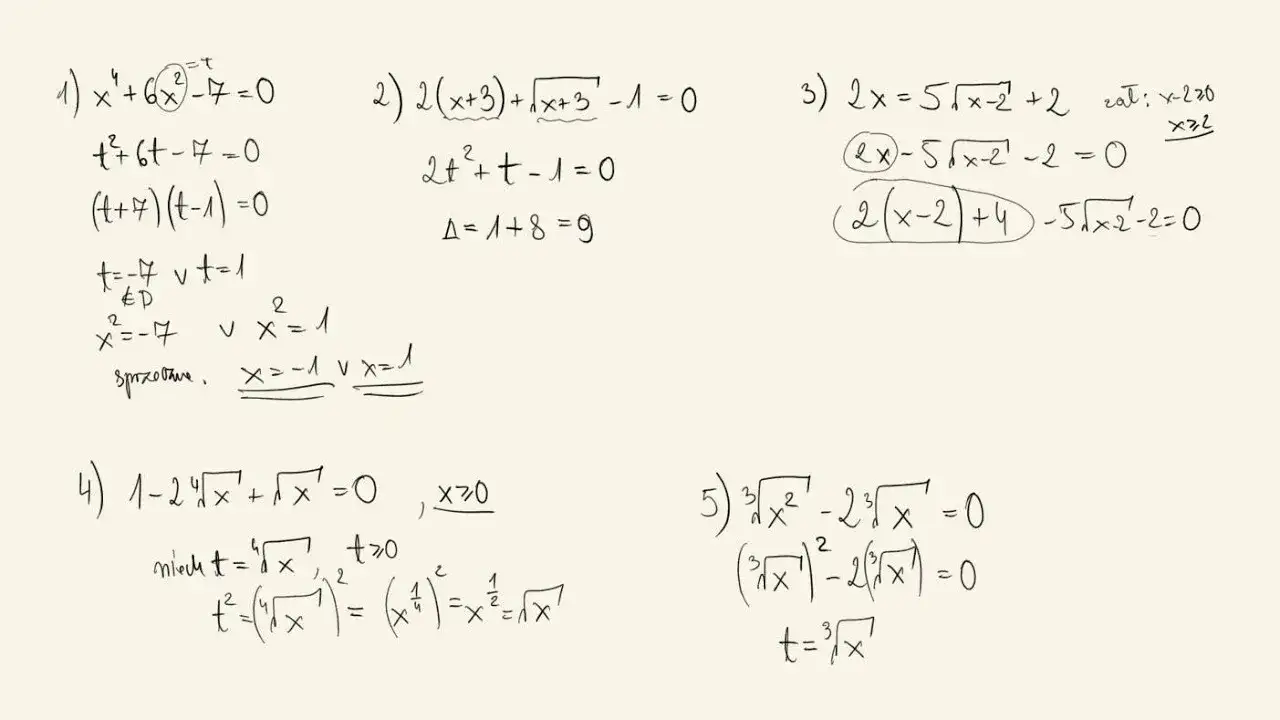Ile rozwiązań ma równanie? To pytanie nurtuje wielu uczniów i studentów, którzy stają przed wyzwaniem rozwiązywania różnych typów równań. Ilość rozwiązań równania zależy od jego rodzaju oraz postaci. Na przykład, równanie liniowe z jedną niewiadomą może mieć jedno rozwiązanie, być tożsamościowe (ma nieskończenie wiele rozwiązań) lub być sprzeczne (nie ma rozwiązań). Zrozumienie tych różnic jest kluczowe dla skutecznego rozwiązywania równań i dalszego zgłębiania matematyki.
W artykule przyjrzymy się różnym typom równań, takim jak równania liniowe i kwadratowe, oraz czynnikom, które wpływają na liczbę ich rozwiązań. Omówimy również przykłady, które pomogą lepiej zrozumieć te zagadnienia. Zrozumienie, jak różne elementy równania wpływają na jego rozwiązania, jest nie tylko istotne w nauce, ale także w praktycznych zastosowaniach w codziennym życiu.
Kluczowe informacje:- Równania liniowe mogą mieć jedno rozwiązanie, nieskończoność rozwiązań lub nie mieć ich wcale.
- Równania kwadratowe są analizowane za pomocą współczynnika D, który określa liczbę rozwiązań.
- Współczynniki równania mają znaczący wpływ na jego rozwiązania.
- Graficzna interpretacja równań pozwala zrozumieć, ile rozwiązań może mieć dane równanie.
- Przykłady równań liniowych i kwadratowych ilustrują różne typy rozwiązań.
Jakie są typy równań i ich charakterystyka rozwiązań?
W matematyce istnieją różne typy równań, które różnią się od siebie pod względem liczby rozwiązań. Dwa z najważniejszych typów to równania liniowe i równania kwadratowe. Każdy z tych typów ma swoje własne cechy, które decydują o tym, ile rozwiązań może mieć dane równanie. W przypadku równań liniowych, liczba rozwiązań może być różna w zależności od tego, jak są one skonstruowane.
Równania liniowe z jedną niewiadomą mogą mieć jedno rozwiązanie, być sprzeczne (co oznacza, że nie mają żadnych rozwiązań) lub być tożsamościowe (mają nieskończoną liczbę rozwiązań). Z kolei równania kwadratowe są bardziej złożone i ich liczba rozwiązań zależy głównie od wartości współczynnika D, znanego jako wyróżnik. Zrozumienie tych różnic jest kluczowe dla dalszego zgłębiania tematu równań i ich zastosowań w praktyce.
Równania liniowe: jedno, sprzeczne lub nieskończoność rozwiązań
Równania liniowe to najprostszy typ równań, które mogą mieć różne liczby rozwiązań. Można je opisać w postaci ogólnej: ax + b = 0, gdzie a i b są stałymi. W zależności od wartości a i b, równania liniowe mogą przyjmować różne formy. Na przykład, jeśli a ≠ 0, równanie ma jedno rozwiązanie. Jeśli jednak a = 0 i b ≠ 0, równanie jest sprzeczne i nie ma rozwiązań. Natomiast, gdy a = 0 i b = 0, równanie jest tożsamościowe i ma nieskończoną liczbę rozwiązań.
- Przykład równania z jednym rozwiązaniem: 2x + 4 = 0 (rozwiązanie: x = -2)
- Przykład równania sprzecznego: 0x + 5 = 0 (brak rozwiązań)
- Przykład równania tożsamościowego: 0x = 0 (nieskończona liczba rozwiązań)
Równania kwadratowe: analiza liczby rozwiązań i ich typów
Równania kwadratowe są bardziej złożone niż równania liniowe i ich liczba rozwiązań zależy od wartości współczynnika D, znanego jako wyróżnik. Wzór ogólny równania kwadratowego ma postać ax² + bx + c = 0, gdzie a, b i c są stałymi. W zależności od wartości D, możemy mieć jedno rozwiązanie, dwa rozwiązania lub brak rozwiązań. Wartość wyróżnika D obliczamy ze wzoru D = b² - 4ac. Gdy D jest większe od zera, równanie ma dwa różne rozwiązania; gdy D równa się zero, rozwiązanie jest jedno; a gdy D jest mniejsze od zera, równanie nie ma rozwiązań.
| Wartość D | Typ rozwiązania | Przykład równania |
|---|---|---|
| D > 0 | Dwa różne rozwiązania | x² - 5x + 6 = 0 (rozwiązania: x = 2, x = 3) |
| D = 0 | Jedno rozwiązanie | x² - 4x + 4 = 0 (rozwiązanie: x = 2) |
| D < 0 | Brak rozwiązań | x² + 4x + 5 = 0 (brak rozwiązań) |
Wpływ współczynników na rozwiązania równań
Współczynniki w równaniach mają kluczowe znaczenie dla określenia liczby rozwiązań. W przypadku równań liniowych, zmiana wartości współczynnika a w równaniu ax + b = 0 może prowadzić do różnych wyników. Jeśli a jest różne od zera, równanie ma jedno rozwiązanie. Natomiast w równaniach kwadratowych, zmiana współczynników a, b i c w równaniu ax² + bx + c = 0 wpływa na wartość wyróżnika D, co z kolei decyduje o liczbie rozwiązań. Na przykład, zwiększenie wartości a może spowodować, że równanie będzie miało dwa rozwiązania zamiast jednego, jeśli wcześniej D było równe zero.
Geometria równań: interpretacja graficzna rozwiązań
Graficzna interpretacja równań pozwala na wizualizację liczby rozwiązań. W przypadku równań liniowych, linia prosta może przeciąć oś x w jednym punkcie (jedno rozwiązanie), nie przecinać jej wcale (brak rozwiązań) lub pokrywać się z osią x (nieskończona liczba rozwiązań). Dla równań kwadratowych, parabola może mieć dwa punkty przecięcia z osią x (dwa rozwiązania), jeden punkt (jedno rozwiązanie) lub nie mieć punktu przecięcia (brak rozwiązań). Zrozumienie tych zależności jest kluczowe dla analizy i rozwiązywania równań w praktyce.
Przykłady równań z różnymi rozwiązaniami
Równania liniowe to jeden z najprostszych typów równań, które można spotkać w matematyce. Mogą mieć różne liczby rozwiązań w zależności od wartości ich współczynników. Na przykład, równanie 2x + 4 = 0 ma jedno rozwiązanie, które można obliczyć jako x = -2. Inne równanie, takie jak 0x + 5 = 0, jest sprzeczne, co oznacza, że nie ma rozwiązań. Z kolei równanie 0x = 0 jest tożsamościowe i ma nieskończoną liczbę rozwiązań. Warto zrozumieć, jak różne formy równań liniowych wpływają na ich rozwiązania.
- Równanie z jednym rozwiązaniem: 3x - 9 = 0 (rozwiązanie: x = 3)
- Równanie sprzeczne: 0x + 1 = 0 (brak rozwiązań)
- Równanie tożsamościowe: 0x = 0 (nieskończona liczba rozwiązań)
Równania kwadratowe są bardziej złożone i ich liczba rozwiązań również zależy od ich współczynników. Dla równania kwadratowego ax² + bx + c = 0, liczba rozwiązań zależy od wartości wyróżnika D. Przykładem równania kwadratowego z dwoma rozwiązaniami jest x² - 5x + 6 = 0, które ma rozwiązania x = 2 i x = 3. Z kolei równanie x² - 4x + 4 = 0 ma jedno rozwiązanie, x = 2, a równanie x² + 4x + 5 = 0 nie ma rozwiązań. Zrozumienie, jak te równania działają, jest kluczowe w matematyce.
- Równanie z dwoma rozwiązaniami: x² - 5x + 6 = 0 (rozwiązania: x = 2, x = 3)
- Równanie z jednym rozwiązaniem: x² - 4x + 4 = 0 (rozwiązanie: x = 2)
- Równanie bez rozwiązań: x² + 4x + 5 = 0 (brak rozwiązań)
Przykłady równań liniowych z różnymi wynikami
Równania liniowe mogą ilustrować różne typy rozwiązań, w zależności od ich współczynników. Na przykład, równanie 3x - 9 = 0 ma jedno rozwiązanie, które można obliczyć jako x = 3. Z kolei równanie 0x + 1 = 0 jest sprzeczne, co oznacza, że nie ma żadnych rozwiązań. Inny przykład to równanie 0x = 0, które jest tożsamościowe i ma nieskończoną liczbę rozwiązań, ponieważ każda wartość x spełnia to równanie. Te różnice w rozwiązaniach pokazują, jak ważne jest zrozumienie struktury równań liniowych.
- Równanie z jednym rozwiązaniem: 4x + 8 = 0 (rozwiązanie: x = -2)
- Równanie sprzeczne: 0x + 3 = 0 (brak rozwiązań)
- Równanie tożsamościowe: 0x = 0 (nieskończona liczba rozwiązań)
Przykłady równań kwadratowych: jedno, dwa i brak rozwiązań
Równania kwadratowe również mogą mieć różne liczby rozwiązań, co zależy od wartości współczynników i wyróżnika D. Na przykład, równanie x² - 5x + 6 = 0 ma dwa rozwiązania: x = 2 i x = 3. Z kolei równanie x² - 4x + 4 = 0 ma jedno rozwiązanie, x = 2, ponieważ wyróżnik D równa się zero. Natomiast równanie x² + 4x + 5 = 0 nie ma rozwiązań, ponieważ D jest mniejsze od zera. Te przykłady pokazują, jak różne formy równań kwadratowych wpływają na liczbę ich rozwiązań.
- Równanie z dwoma rozwiązaniami: x² - 5x + 6 = 0 (rozwiązania: x = 2, x = 3)
- Równanie z jednym rozwiązaniem: x² - 4x + 4 = 0 (rozwiązanie: x = 2)
- Równanie bez rozwiązań: x² + 4x + 5 = 0 (brak rozwiązań)
Czytaj więcej: Najpopularniejsze zawody do pracy zdalnej - poznaj 10 najlepszych opcji
Praktyczne zastosowania równań w codziennym życiu i technologii
Równania, zarówno liniowe, jak i kwadratowe, mają wiele praktycznych zastosowań w codziennym życiu oraz w różnych dziedzinach technologii. Na przykład, w inżynierii i architekturze, równania kwadratowe są wykorzystywane do obliczania trajektorii obiektów, co jest kluczowe przy projektowaniu mostów czy budynków. Dzięki zrozumieniu, jak różne współczynniki wpływają na rozwiązania równań, inżynierowie mogą optymalizować struktury, aby były bardziej wytrzymałe i efektywne.
W codziennym życiu, znajomość równań liniowych może pomóc w zarządzaniu budżetem domowym. Na przykład, można użyć równań do obliczenia, jak zmiana wydatków wpływa na oszczędności. Warto również zauważyć, że w erze cyfrowej, algorytmy oparte na równaniach matematycznych są podstawą wielu aplikacji, od prognozowania pogody po systemy rekomendacji w e-commerce. Zrozumienie tych równań daje przewagę w analizie danych i podejmowaniu lepszych decyzji.
