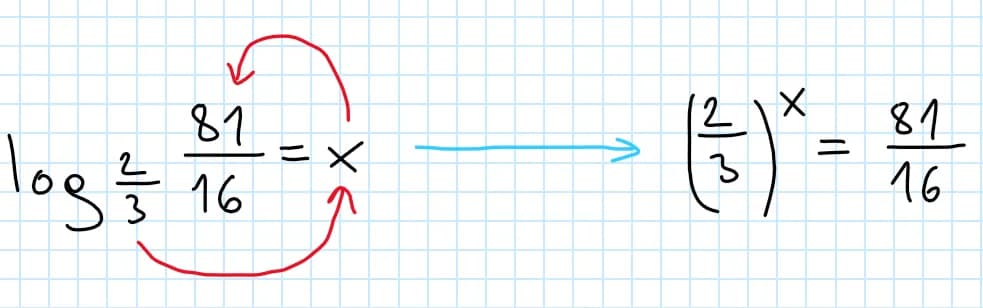
Obliczanie logarytmu z pierwiastkiem może wydawać się skomplikowane, ale w rzeczywistości jest to proces, który można zrozumieć dzięki kilku prostym zasadom. Logarytm to funkcja matematyczna, która pozwala nam zrozumieć, jak wiele razy musimy pomnożyć pewną liczbę, aby uzyskać inną liczbę. W przypadku pierwiastków, sytuacja staje się jeszcze bardziej interesująca, ponieważ możemy je przekształcić w potęgowanie, co ułatwia obliczenia.
Na przykład, aby obliczyć logarytm z pierwiastka, takiego jak log√55, możemy zapisać to jako równanie potęgowe. Dzięki tej metodzie, możemy łatwo znaleźć wartość logarytmu, co pokazuje, że zrozumienie podstawowych właściwości logarytmów i pierwiastków jest kluczem do skutecznych obliczeń. W tym artykule przedstawimy różne metody obliczania logarytmu z pierwiastkiem oraz przykłady, które pomogą w lepszym zrozumieniu tematu.
Kluczowe wnioski:- Logarytm to funkcja, która określa, ile razy należy pomnożyć podstawę, aby uzyskać daną liczbę.
- Pierwiastek można przekształcić w potęgowanie, co ułatwia obliczenia logarytmiczne.
- Przykład log√55 pokazuje, jak zamiana na potęgę prowadzi do prostych równań.
- Właściwości logarytmów, takie jak zasady mnożenia i dzielenia, pomagają w uproszczeniu obliczeń.
- Wizualizacja obliczeń, np. za pomocą wykresów, może ułatwić zrozumienie logarytmów i pierwiastków.
Jak obliczyć logarytm z pierwiastkiem - podstawowe pojęcia i definicje
Logarytm to funkcja matematyczna, która określa, ile razy należy pomnożyć podstawę, aby uzyskać daną liczbę. Jest to kluczowy element w matematyce, który znajduje zastosowanie w różnych dziedzinach, od nauk ścisłych po ekonomię. W kontekście pierwiastków, logarytmy stają się jeszcze bardziej interesujące, ponieważ pozwalają na przekształcanie wyrażeń matematycznych w bardziej zrozumiałe formy. Zrozumienie tych podstawowych pojęć jest niezbędne do skutecznego rozwiązywania problemów związanych z logarytmami.
Pierwiastek, z kolei, to operacja odwrotna do potęgowania. Obliczanie pierwiastków polega na znalezieniu liczby, która po podniesieniu do określonej potęgi daje daną wartość. Na przykład, pierwiastek kwadratowy z liczby 16 to 4, ponieważ 4^2 = 16. W przypadku logarytmów z pierwiastkami, kluczowe jest zrozumienie, jak te dwie koncepcje współdziałają, co umożliwia przekształcanie logarytmów do postaci potęgowej, co znacząco upraszcza obliczenia.Logarytm - definicja i właściwości, które musisz znać
Logarytm można zdefiniować jako funkcję, która odpowiada na pytanie, ile razy należy pomnożyć podstawę, aby uzyskać daną liczbę. Istnieją różne typy logarytmów, w tym logarytmy naturalne i dziesiętne. Właściwości logarytmów, takie jak zasady mnożenia, dzielenia i potęgowania, są fundamentalne dla ich zastosowań. Na przykład, zasada mnożenia logarytmów mówi, że logarytm iloczynu dwóch liczb jest równy sumie logarytmów tych liczb. To sprawia, że obliczenia stają się prostsze i bardziej przejrzyste.Warto również zauważyć, że logarytmy mają zastosowanie w wielu dziedzinach matematyki i nauki. Umożliwiają one analizę wykresów, obliczanie wartości w równaniach oraz rozwiązywanie złożonych problemów. Zrozumienie tych właściwości jest kluczowe dla każdego, kto chce skutecznie pracować z logarytmami i pierwiastkami, a także dla tych, którzy pragną zgłębiać bardziej zaawansowane zagadnienia matematyczne.
Pierwiastek - co to jest i jak go obliczać w matematyce
Pierwiastek to operacja matematyczna, która polega na znalezieniu liczby, która po podniesieniu do danej potęgi daje określoną wartość. Na przykład, pierwiastek kwadratowy z liczby 16 to 4, ponieważ 4^2 = 16. W matematyce, pierwiastki są kluczowe w wielu obliczeniach, szczególnie w kontekście logarytmów. Zrozumienie, jak obliczać pierwiastki, jest niezbędne dla efektywnego rozwiązywania równań i problemów matematycznych.
Aby obliczyć pierwiastek, można skorzystać z różnych metod. Najczęściej stosowaną metodą jest użycie kalkulatora, który automatycznie oblicza pierwiastki. Można również korzystać z tablic pierwiastków lub programów komputerowych. Warto pamiętać, że istnieją również różne typy pierwiastków, takie jak pierwiastek kwadratowy, sześcienny czy wyższych rzędów, które mają swoje specyficzne zastosowania w matematyce.
Metody obliczania logarytmu z pierwiastkiem - krok po kroku
Obliczanie logarytmu z pierwiastkiem może być proste, gdy zrozumie się podstawowe zasady. Pierwszym krokiem jest przekształcenie logarytmu w formę potęgowania. Na przykład, aby obliczyć log√55, można zapisać to jako równanie: (√5)x = 5. Następnie, przekształcamy pierwiastek do postaci potęgowej: (51/2)x = 5. Po uproszczeniu, otrzymujemy 5x/2 = 5, co pozwala nam na dalsze obliczenia.
Ważne jest, aby pamiętać, że logarytmy mają swoje zasady, które mogą ułatwić obliczenia. Na przykład, zasada mnożenia logarytmów mówi, że logarytm iloczynu dwóch liczb jest równy sumie logarytmów tych liczb. Dzięki temu, można łatwo rozwiązywać bardziej złożone równania, które zawierają pierwiastki. Używając tych metod, można efektywnie obliczać logarytmy z pierwiastkami w różnych kontekstach matematycznych.
Przykład 1: Logarytm z pierwiastka kwadratowego - prosta metoda
Aby obliczyć logarytm z pierwiastka kwadratowego, weźmy przykład log(√16). Najpierw przekształcamy pierwiastek do postaci potęgowej: √16 można zapisać jako 161/2. Teraz mamy do czynienia z równaniem: log(161/2). Zastosujemy zasadę potęgowania logarytmu, która mówi, że log(an) = n * log(a). W naszym przypadku to oznacza, że log(161/2) = (1/2) * log(16).
Teraz musimy obliczyć log(16). Ponieważ 16 to 42 i 4 to 22, możemy zapisać log(16) jako log(42) = 2 * log(4). Następnie, log(4) można obliczyć jako log(22) = 2 * log(2). Ostatecznie, łącząc wszystkie te informacje, otrzymujemy: log(√16) = (1/2) * (2 * 2 * log(2)) = 2 * log(2). Tak więc, log(√16) = 2 * log(2).
Przykład 2: Logarytm z pierwiastka sześciennego - szczegółowe obliczenia
Rozważmy teraz obliczenie logarytmu z pierwiastka sześciennego, na przykład log(∛27). Pierwiastek sześcienny z 27 możemy zapisać jako 271/3. Stosując tę samą zasadę potęgowania, mamy: log(271/3) = (1/3) * log(27).
Teraz obliczamy log(27). Ponieważ 27 to 33, możemy zapisać log(27) jako log(33) = 3 * log(3). Wstawiając to do naszego równania, otrzymujemy: log(∛27) = (1/3) * (3 * log(3)). Po uproszczeniu, dostajemy log(∛27) = log(3). Tak więc, log(∛27) = log(3) jest ostatecznym wynikiem tego obliczenia.
Czytaj więcej: Trzymanie rąk za plecami: Co mówi o Tobie ten gest?
Właściwości logarytmów - jak ułatwiają obliczenia z pierwiastkami
Właściwości logarytmów są kluczowe w matematyce, ponieważ upraszczają obliczenia związane z pierwiastkami. Dwie najważniejsze właściwości to zasady mnożenia i dzielenia logarytmów oraz zasada potęgowania. Te reguły pozwalają na przekształcanie skomplikowanych wyrażeń logarytmicznych w prostsze formy, co ułatwia ich obliczanie. Na przykład, zamiast obliczać logarytm z iloczynu, można obliczyć logarytmy poszczególnych składników i je dodać, co znacząco przyspiesza proces obliczeń.
W kontekście pierwiastków, zasady te mają szczególne znaczenie. Umożliwiają one przekształcanie logarytmów z pierwiastkami do postaci, która jest łatwiejsza do obliczenia. Dzięki tym regułom, można zredukować złożoność obliczeń, co jest szczególnie przydatne w bardziej zaawansowanych zagadnieniach matematycznych. Zrozumienie i umiejętność stosowania tych właściwości jest niezbędne dla każdego, kto chce efektywnie korzystać z logarytmów w praktyce.
Zasada mnożenia i dzielenia logarytmów - zastosowanie w praktyce
Zasada mnożenia logarytmów mówi, że logarytm iloczynu dwóch liczb jest równy sumie logarytmów tych liczb. Na przykład, dla loga(b * c) możemy zapisać to jako loga(b) + loga(c). Ta zasada jest niezwykle użyteczna, gdyż pozwala na uproszczenie obliczeń logarytmicznych, zwłaszcza w przypadku pierwiastków. Podobnie, zasada dzielenia logarytmów mówi, że logarytm ilorazu dwóch liczb jest równy różnicy logarytmów tych liczb: loga(b / c) = loga(b) - loga(c).
Przykładem zastosowania tych zasad może być obliczenie logarytmu z pierwiastków. Na przykład, jeśli mamy do obliczenia log2(√8 * √4), możemy najpierw przekształcić to do postaci log2(√8) + log2(√4). Następnie, obliczając każdy z logarytmów osobno, uprościmy całe wyrażenie. Zastosowanie tych zasad nie tylko przyspiesza obliczenia, ale także czyni je bardziej przejrzystymi i zrozumiałymi.
Zasada potęgowania logarytmów - przydatne techniki obliczeniowe
Zasada potęgowania logarytmów jest jedną z kluczowych właściwości, która ułatwia obliczenia związane z logarytmami, szczególnie gdy mamy do czynienia z pierwiastkami. Mówi ona, że logarytm liczby podniesionej do potęgi można obliczyć jako iloczyn potęgi i logarytmu tej liczby. Na przykład, dla loga(bn) możemy zapisać to jako n * loga(b). Ta zasada jest niezwykle pomocna, gdyż pozwala na uproszczenie skomplikowanych równań logarytmicznych.Przykład zastosowania tej zasady można zobaczyć w obliczeniach logarytmicznych z pierwiastkami. Jeśli chcemy obliczyć log2(√8), możemy najpierw zapisać pierwiastek w formie potęgowej: √8 = 81/2. Następnie, stosując zasadę potęgowania, otrzymujemy: log2(√8) = log2(81/2) = (1/2) * log2(8). Ponieważ 8 to 23, możemy dalej uprościć to do (1/2) * log2(23) = (1/2) * 3 = 3/2. Tak więc, log2(√8) = 3/2, co pokazuje, jak zasada potęgowania może znacznie ułatwić obliczenia.
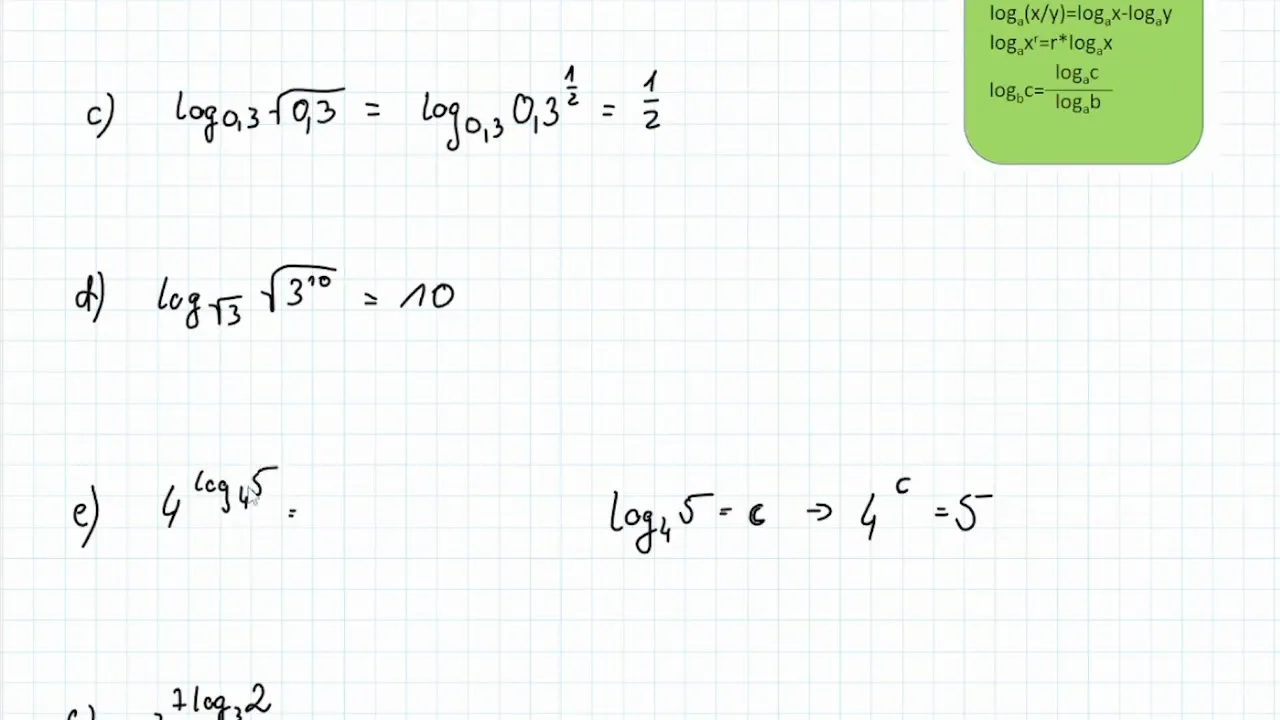
Wizualizacja obliczeń - jak diagramy mogą pomóc w nauce
Wizualizacja obliczeń jest kluczowym narzędziem, które może znacznie ułatwić zrozumienie koncepcji logarytmów oraz pierwiastków. Diagramy i wykresy pomagają zobrazować relacje między różnymi wartościami, co sprawia, że trudne pojęcia stają się bardziej przystępne. W kontekście logarytmów, wizualizacja może pomóc w zrozumieniu, jak zmieniają się wartości logarytmiczne w odpowiedzi na zmiany w podstawie lub argumentach logarytmu.
Używając wizualizacji, można również lepiej zrozumieć, jak pierwiastki wpływają na obliczenia logarytmiczne. Na przykład, wykresy funkcji logarytmicznych mogą pokazywać, jak różne podstawy logarytmu zmieniają krzywą wykresu. Takie wizualizacje mogą być szczególnie pomocne w nauczaniu, ponieważ pozwalają uczniom na lepsze zrozumienie, jak te koncepcje są ze sobą powiązane i jak można je zastosować w praktyce.
Graficzne przedstawienie logarytmów i pierwiastków - praktyczne przykłady
Graficzne przedstawienie logarytmów i pierwiastków może być niezwykle pomocne w nauce matematyki. Aby stworzyć wykres logarytmu, można użyć programów takich jak Excel lub GeoGebra, które umożliwiają łatwe rysowanie funkcji. Na przykład, wykres funkcji y = log2(x) pokazuje, jak wartość logarytmu zmienia się w zależności od argumentu x. Można również porównać wykresy różnych podstaw logarytmu, co pozwala na lepsze zrozumienie ich zachowania.
- Wykresy logarytmiczne mogą ilustrować zmiany wartości logarytmu w odpowiedzi na zmiany podstawy.
- Można porównywać różne funkcje logarytmiczne, aby zobaczyć, jak różne podstawy wpływają na kształt wykresu.
- Wizualizacje mogą być używane do nauki o pierwiastkach, pokazując, jak pierwiastki wpływają na wartości logarytmiczne.
| Podstawa logarytmu | Logarytm z pierwiastka 16 |
| 2 | 4 |
| 3 | 2.6667 |
| 5 | 2 |
Wykresy funkcji logarytmicznych - zrozumienie ich znaczenia
Wykresy funkcji logarytmicznych są nie tylko narzędziem do wizualizacji, ale także kluczowym elementem w analizie matematycznej. Pomagają one w zrozumieniu, jak logarytmy zachowują się w różnych zakresach wartości. Na przykład, wykres log10(x) pokazuje, że dla małych wartości x, logarytm rośnie powoli, a dla dużych wartości rośnie szybciej. To zrozumienie jest istotne w kontekście obliczeń, gdzie zmiany w argumentach logarytmu mogą mieć znaczący wpływ na wyniki.
Analizując wykresy, można zauważyć, że logarytmy mają charakterystyczne punkty, takie jak punkty przecięcia z osią y, które odpowiadają wartościom logarytmu dla x = 1. Te punkty są istotne, ponieważ pomagają w szybkiej ocenie wartości logarytmów bez konieczności ich dokładnego obliczania. Zrozumienie wykresów logarytmicznych i ich znaczenia w kontekście pierwiastków jest kluczowe dla każdej osoby, która chce zgłębiać matematykę na wyższym poziomie.
Jak wykorzystać logarytmy w analizie danych i statystyce
Logarytmy mają szerokie zastosowanie nie tylko w matematyce teoretycznej, ale również w praktycznych dziedzinach, takich jak analiza danych i statystyka. W kontekście analizy danych, logarytmy są często używane do transformacji danych, co może pomóc w normalizacji rozkładów i ułatwieniu wykrywania wzorców. Na przykład, w przypadku danych o dużym zakresie wartości, takich jak dochody lub populacje, zastosowanie logarytmu może przekształcić te dane w bardziej zrozumiałą formę, co ułatwi ich analizę i wizualizację.
W statystyce, logarytmy są również kluczowe w modelowaniu regresji, szczególnie w przypadku modeli, które wymagają analizy wzrostu lub spadku wartości w czasie. Dzięki zastosowaniu logarytmu, można uzyskać liniowe relacje z danych, które w przeciwnym razie mogłyby być nieliniowe. Wykorzystanie logarytmów w tej dziedzinie nie tylko zwiększa precyzję obliczeń, ale także umożliwia lepsze prognozowanie i podejmowanie decyzji opartych na danych. Warto zatem zgłębiać tę tematykę, aby w pełni wykorzystać potencjał logarytmów w różnych zastosowaniach praktycznych.