Wysokość w trójkącie różnobocznym jest kluczowym elementem w geometrii, który można obliczyć za pomocą prostego wzoru. Aby znaleźć wysokość, potrzebne są dwie wartości: długość podstawy oraz pole trójkąta. Wzór, który stosujemy, to h = 2A/b, gdzie A to pole, a b to długość podstawy. Dzięki temu prostemu równaniu możemy szybko i efektywnie określić wysokość trójkąta różnobocznego.
W artykule omówimy, jak krok po kroku obliczyć wysokość w trójkącie różnobocznym. Przedstawimy również przykłady, które pomogą zrozumieć ten proces, oraz wizualizacje, które ułatwią naukę. Niezależnie od tego, czy jesteś uczniem, czy po prostu chcesz przypomnieć sobie zasady geometrii, nasze wskazówki będą przydatne.
Kluczowe informacje:- Wysokość w trójkącie różnobocznym oblicza się za pomocą wzoru h = 2A/b.
- Do obliczenia wysokości potrzebne są wartości podstawy i pola trójkąta.
- W artykule znajdziesz praktyczne przykłady obliczeń wysokości w różnych trójkątach.
- Wizualizacje pomogą lepiej zrozumieć proces obliczania wysokości.
- Wysokość trójkąta różnobocznego można obliczyć na podstawie długości boków oraz pola.
Jak obliczyć wysokość w trójkącie różnobocznym - krok po kroku
Obliczenie wysokości w trójkącie różnobocznym jest kluczowym aspektem geometrii, który można wykonać w kilku prostych krokach. Wysokość, oznaczana jako h, można znaleźć przy użyciu wzoru h = 2A/b, gdzie A to pole trójkąta, a b to długość jego podstawy. Ta metoda umożliwia dokładne określenie wysokości, co jest istotne w wielu zastosowaniach, od obliczeń w szkole po praktyczne zastosowania w inżynierii.
Aby obliczyć wysokość, należy najpierw znać pole trójkąta oraz długość podstawy. Kiedy te wartości są dostępne, wystarczy podstawić je do wzoru. Proces jest prosty i zrozumiały, co czyni go dostępnym dla każdego, kto chce nauczyć się podstaw geometrii. W kolejnych częściach artykułu szczegółowo omówimy, jak zastosować ten wzór w różnych scenariuszach, aby jeszcze lepiej zrozumieć, jak obliczyć wysokość w trójkącie różnobocznym.
Zrozumienie podstawowych pojęć dotyczących trójkątów różnobocznych
Trójkąty różnoboczne to figury geometryczne, w których wszystkie boki mają różne długości. W przeciwieństwie do trójkątów równobocznych, w których wszystkie boki są równe, oraz trójkątów równoramiennych, które posiadają dwa boki o tej samej długości, trójkąty różnoboczne charakteryzują się unikalnością każdego z boków. To sprawia, że obliczenia związane z ich wysokością, polem czy innymi właściwościami geometrycznymi mogą być bardziej skomplikowane, ale również bardziej interesujące.
W trójkącie różnobocznym nie tylko długości boków są różne, ale także kąty wewnętrzne. Każdy z tych kątów może mieć inną miarę, co wpływa na kształt i proporcje trójkąta. Zrozumienie tych podstawowych pojęć jest kluczowe dla dalszego zgłębiania tematu obliczania wysokości oraz innych właściwości trójkątów różnobocznych.
Wzór na wysokość w trójkącie różnobocznym - prosty i skuteczny
Wysokość w trójkącie różnobocznym można obliczyć za pomocą prostego wzoru: h = 2A/b. W tym równaniu A oznacza pole trójkąta, a b to długość podstawy. Zrozumienie tego wzoru jest kluczowe, ponieważ pozwala na szybkie i efektywne obliczenie wysokości, co jest istotne w różnych zastosowaniach matematycznych i inżynieryjnych.
Każdy z elementów wzoru ma swoje znaczenie. Pole trójkąta, A, można obliczyć na różne sposoby, w zależności od dostępnych danych, a długość podstawy b jest łatwa do zmierzenia. Korzystając z tego wzoru, możemy nie tylko obliczyć wysokość trójkąta, ale także lepiej zrozumieć jego właściwości geometryczne. To narzędzie jest niezwykle przydatne dla uczniów i profesjonalistów zajmujących się geometrią.
Przykłady obliczania wysokości w różnych trójkątach różnobocznych
Obliczanie wysokości w trójkącie różnobocznym może być łatwiejsze, gdy mamy konkretne przykłady. W tej sekcji przedstawimy różne scenariusze, w których zastosujemy wzór do obliczenia wysokości. Przykłady te pomogą lepiej zrozumieć, jak wykorzystać wzór h = 2A/b w praktyce.
W pierwszym przykładzie rozważmy trójkąt o podstawie 5 cm i polu równym 20 cm². Podstawiając te wartości do wzoru, obliczymy wysokość. W drugim przykładzie weźmiemy trójkąt z innymi wymiarami, aby pokazać, jak wzór działa w różnych sytuacjach. Umożliwi to zobaczenie, jak różne dane wpływają na wynik obliczeń.
| Długość podstawy (b) | Pole (A) | Obliczona wysokość (h) |
| 5 cm | 20 cm² | 8 cm |
| 6 cm | 18 cm² | 6 cm |
Obliczanie wysokości przy znanej podstawie i polu trójkąta
Aby obliczyć wysokość w trójkącie różnobocznym, gdy znamy długość podstawy oraz pole, możemy wykorzystać wzór h = 2A/b. W tym równaniu A to pole trójkąta, a b to długość podstawy. Na przykład, jeśli mamy trójkąt o podstawie 6 cm i polu 24 cm², podstawiamy te wartości do wzoru. Obliczamy wysokość, co daje nam wynik: h = 2 * 24 / 6 = 8 cm.
Warto zauważyć, że znajomość zarówno podstawy, jak i pola trójkąta jest kluczowa dla uzyskania dokładnych wyników. Obliczając wysokość w ten sposób, możemy lepiej zrozumieć, jak różne wymiary wpływają na kształt trójkąta oraz jego właściwości. To podejście jest szczególnie przydatne w zadaniach geometrycznych oraz w praktycznych zastosowaniach w inżynierii.
Wysokość trójkąta różnobocznego przy danych długościach boków
Obliczenie wysokości trójkąta różnobocznego, gdy znamy długości wszystkich trzech boków, jest możliwe przy użyciu wzoru Herona do obliczenia pola. Po pierwsze, obliczamy półobwód s trójkąta, korzystając z wzoru s = (a + b + c) / 2, gdzie a, b, i c to długości boków. Następnie pole A można obliczyć jako A = √(s(s-a)(s-b)(s-c)). Po uzyskaniu pola, możemy użyć wzoru na wysokość h = 2A/b, wybierając dowolną stronę jako podstawę.
Na przykład, dla trójkąta o bokach 5 cm, 6 cm i 7 cm, najpierw obliczamy półobwód: s = (5 + 6 + 7) / 2 = 9. Następnie obliczamy pole: A = √(9(9-5)(9-6)(9-7)) = √(9 * 4 * 3 * 2) = √(216) ≈ 14.7 cm². Wybierając bok 6 cm jako podstawę, obliczamy wysokość: h = 2 * 14.7 / 6 ≈ 4.9 cm. Takie podejście pozwala na elastyczność w obliczeniach i lepsze zrozumienie geometrii trójkątów różnobocznych.
Czytaj więcej: Kwalifikacje psychologa szkolnego - co musisz spełnić by dostać pracę
Wizualizacja obliczeń - jak lepiej zrozumieć proces
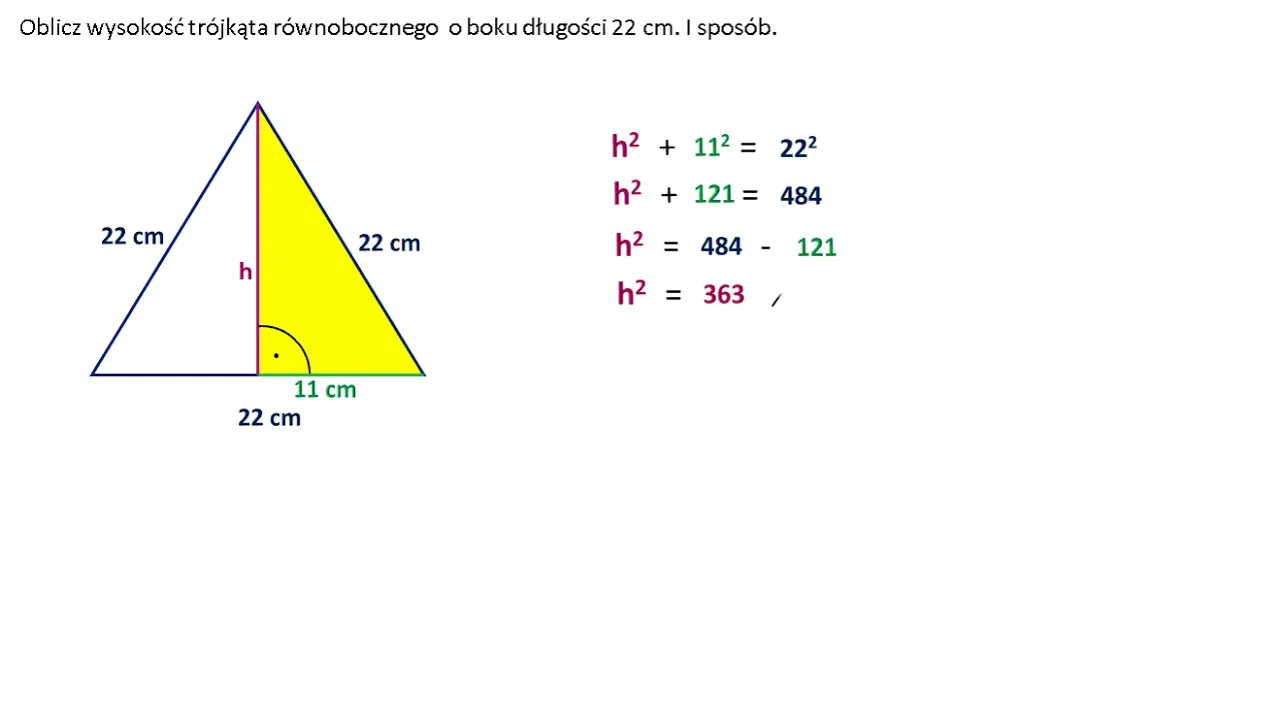
Wizualizacja obliczeń jest niezwykle ważna w matematyce, szczególnie w kontekście obliczania wysokości w trójkącie różnobocznym. Użycie diagramów i rysunków może znacząco ułatwić zrozumienie, jak różne elementy trójkąta wpływają na obliczenia. Dzięki wizualnym przedstawieniom możemy szybko zidentyfikować boki, kąty oraz wysokość, co przyczynia się do lepszego przyswajania wiedzy i umiejętności praktycznych.
Wizualizacje pomagają również w nauce poprzez umożliwienie uczniom zobaczenia, jak wzory i obliczenia przekładają się na rzeczywiste kształty. Rysunki mogą być używane do ilustrowania różnych scenariuszy obliczeniowych, co czyni proces bardziej interaktywnym i angażującym. W kolejnych częściach artykułu omówimy, jak tworzyć i interpretować diagramy, aby jeszcze bardziej ułatwić zrozumienie obliczeń wysokości w trójkącie różnobocznym.
Graficzne przedstawienie trójkąta różnobocznego i jego wysokości
Podczas tworzenia graficznych przedstawień trójkąta różnobocznego, ważne jest, aby uwzględnić wszystkie istotne elementy. Powinny znaleźć się na nim długości boków, kąty oraz wysokość, która jest zazwyczaj rysowana jako linia prostopadła do podstawy. Taki rysunek nie tylko ułatwia zrozumienie, jak obliczyć wysokość, ale także pokazuje, jak różne wymiary wpływają na kształt trójkąta.
W diagramie warto zaznaczyć również oznaczenia dla każdej z długości boków oraz pola trójkąta. Dzięki temu uczniowie mogą łatwiej zrozumieć, jak zastosować wzór h = 2A/b w praktyce. Prawidłowe oznaczenie elementów na diagramie jest kluczowe dla skutecznej nauki i zrozumienia geometrii trójkątów różnobocznych.
Przykłady wizualne z obliczeniami dla różnych przypadków
Wizualne przykłady obliczania wysokości w trójkątach różnobocznych są niezwykle pomocne w zrozumieniu, jak zastosować wzory w praktyce. Przykłady te pokazują, jak różne długości boków i pola wpływają na wysokość trójkąta. Dzięki tym wizualizacjom można lepiej zobaczyć, jak zmiany w wymiarach wpływają na obliczenia, co jest pomocne zarówno dla uczniów, jak i dla osób pracujących w dziedzinach inżynieryjnych.
W poniższej tabeli przedstawiono różne przypadki trójkątów, w których obliczono wysokości na podstawie znanych długości boków oraz pól. Tego rodzaju zestawienie wizualne ułatwia porównanie wyników oraz zrozumienie, jak różne parametry wpływają na wysokość. Takie podejście jest kluczowe dla przyswajania wiedzy w zakresie geometrii trójkątów różnobocznych.
| Długości boków (a, b, c) | Pole (A) | Obliczona wysokość (h) |
| 5 cm, 6 cm, 7 cm | 14.7 cm² | 4.9 cm |
| 8 cm, 10 cm, 12 cm | 38.8 cm² | 7.6 cm |
Jak wykorzystać wysokość trójkąta do obliczeń w inżynierii
Wysokość trójkąta różnobocznego ma wiele praktycznych zastosowań w inżynierii, architekturze oraz projektowaniu. Znajomość wysokości trójkąta pozwala na obliczenie nie tylko jego pola, ale również objętości różnych struktur, takich jak dachy, zbiorniki czy elementy nośne. W praktyce, inżynierowie często wykorzystują wzory geometryczne do określenia stabilności budowli oraz rozkładu sił w konstrukcjach, co jest kluczowe dla zapewnienia bezpieczeństwa i trwałości.
Dodatkowo, umiejętność obliczania wysokości trójkąta może być używana w nowoczesnych technologiach, takich jak modelowanie 3D i symulacje komputerowe. Dzięki tym technikom, projektanci mogą wizualizować i analizować różne scenariusze, co pozwala na optymalizację projektów przed ich realizacją. Warto zatem rozwijać umiejętności związane z geometrią, aby móc skutecznie stosować je w praktycznych aspektach inżynieryjnych i architektonicznych.
